Преобразования Фурье и обратного Фурье

На этой странице показан рабочий процесс преобразования Фурье и обратного преобразования Фурье в символьных математических Toolbox™. Простые примеры см. в разделе fourier и ifourier. Здесь последовательность операций для преобразований Фурье демонстрируется вычислением отклонения луча из-за силы. Связанное дифференциальное уравнение решается преобразованием Фурье.

Определение преобразования Фурье

Преобразование Фурье f (x) относительно x при w равно

$F (w)_{}^{} =∫−∞∞f (^{x) e} -$ iwxdx.

Обратное преобразование Фурье

$f (x) \frac{}{}_{}^{} =12π∫−∞∞F (^{w)}$ eiwxdw.

Концепция: Использование символьных рабочих процессов

Символьные рабочие процессы содержат вычисления в натуральной символической форме, а не в числовой. Этот подход помогает понять свойства решения и использовать точные символьные значения. Числа подставляются вместо символьных переменных только в том случае, если требуется числовой результат или невозможно продолжить символьно. Дополнительные сведения см. в разделе Выбор числовой или символьной арифметики. Обычно этапы:

Объявить уравнения.
Решите уравнения.
Подстановочные значения.
Результаты графика.
Анализ результатов.

Расчет отклонения балки с помощью преобразования Фурье

Определение уравнений

Преобразование Фурье может использоваться для решения обыкновенных и дифференциальных уравнений в частных производных. Например, можно смоделировать отклонение бесконечно длинной балки, опирающейся на упругое основание под действием точечной силы. Соответствующий реальный пример - железнодорожные пути на фундаменте. Железнодорожные пути являются бесконечно длинной балкой, в то время как фундамент является эластичным.

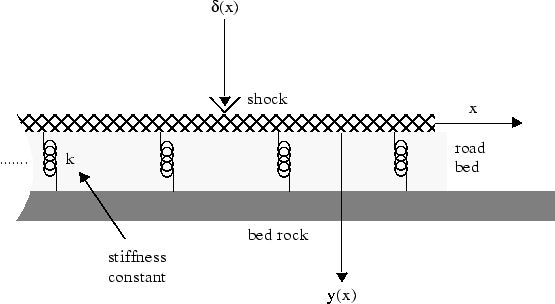
Давайте

E - эластичность балки (или железнодорожного пути).
Я являюсь вторым моментом площади поперечного сечения луча.
k - жесткость основания от пружины.

Дифференциальное уравнение

$\frac{^{}}{^{d4ydx4}} \frac{+}{} \frac{kEIy}{=} 1EIδ (x),$ −∞<x<∞.

Определение функции y(x) и переменные. Принять E, I, и k являются положительными.

syms Y(x) w E I k f
assume([E I k] > 0)

Назначение единиц переменным с помощью symunit.

u = symunit;
Eu = E*u.Pa;    % Pascal
Iu = I*u.m^4;   % meter^4
ku = k*u.N/u.m^2;  % Newton/meter^2
X = x*u.m;
F = f*u.N/u.m;

Определите дифференциальное уравнение.

eqn = diff(Y,X,4) + ku/(Eu*Iu)*Y == F/(Eu*Iu)

eqn(x) =
diff(Y(x), x, x, x, x)*(1/[m]^4) + ((k*Y(x))/(E*I))*([N]/([Pa]*[m]^6)) == ...
        (f/(E*I))*([N]/([Pa]*[m]^5))

Представление силы f дельта-функцией Дирака δ (x).

eqn = subs(eqn,f,dirac(x))

eqn(x) =
diff(Y(x), x, x, x, x)*(1/[m]^4) + ((k*Y(x))/(E*I))*([N]/([Pa]*[m]^6)) == ...
        (dirac(x)/(E*I))*([N]/([Pa]*[m]^5))

Уравнения решения

Вычислите преобразование Фурье eqn с помощью fourier по обе стороны от eqn. Преобразование Фурье преобразует дифференциацию в экспоненты w.

eqnFT = fourier(lhs(eqn)) == fourier(rhs(eqn))

eqnFT =
w^4*fourier(Y(x), x, w)*(1/[m]^4) + ((k*fourier(Y(x), x, w))/(E*I))*([N]/([Pa]*[m]^6)) ...
        == (1/(E*I))*([N]/([Pa]*[m]^5))

Одинокий fourier(Y(x),x,w) в уравнении.

eqnFT = isolate(eqnFT, fourier(Y(x),x,w))

eqnFT =
fourier(Y(x), x, w) == (1/(E*I*w^4*[Pa]*[m]^2 + k*[N]))*[N]*[m]

Вычислить Y(x) вычислением обратного преобразования Фурье правой стороны. Упростите результат.

YSol = ifourier(rhs(eqnFT));
YSol = simplify(YSol)

YSol =
((exp(-(2^(1/2)*k^(1/4)*abs(x))/(2*E^(1/4)*I^(1/4)))*sin((2*2^(1/2)*k^(1/4)*abs(x) + ...
        pi*E^(1/4)*I^(1/4))/(4*E^(1/4)*I^(1/4))))/(2*E^(1/4)*I^(1/4)*k^(3/4)))*[m]

Проверьте, что YSol имеет правильные размеры путем замены YSol в eqn и с использованием checkUnits функция. checkUnits возвращает логический 1 (true), значение eqn теперь имеет совместимые единицы одинаковых физических размеров.

checkUnits(subs(eqn,Y,YSol))

ans = 
  struct with fields:

    Consistent: 1
    Compatible: 1

Отделите выражение от единиц измерения с помощью separateUnits.

YSol = separateUnits(YSol)

YSol =
(exp(-(2^(1/2)*k^(1/4)*abs(x))/(2*E^(1/4)*I^(1/4)))*sin((2*2^(1/2)*k^(1/4)*abs(x) + ...
        pi*E^(1/4)*I^(1/4))/(4*E^(1/4)*I^(1/4))))/(2*E^(1/4)*I^(1/4)*k^(3/4))

Подстановочные значения

Используйте значения E = ¹⁰⁶ Па, I = ^10-3 ^м4 и k = ¹⁰⁶ ^N/m2. Заменить эти значения на YSol и преобразовать в плавающую точку с помощью vpa с 16 цифрами точности.

values = [1e6 1e-3 1e5];
YSol = subs(YSol,[E I k],values);
YSol = vpa(YSol,16)

YSol =
0.0000158113883008419*exp(-2.23606797749979*abs(x))*sin(2.23606797749979*abs(x) + ...
        0.7853981633974483)

Результаты графика

Постройте график результата с помощью fplot.

fplot(YSol)
xlabel('x')
ylabel('Deflection y(x)')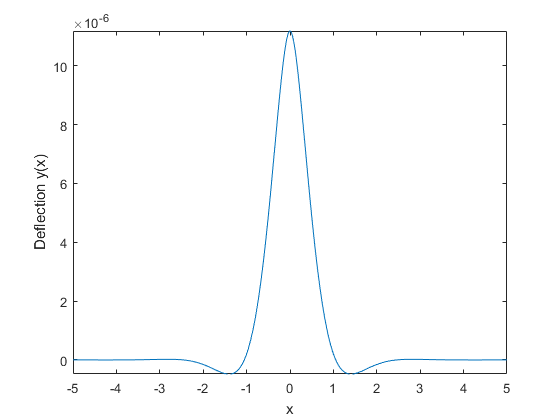

Анализ результатов

График показывает, что отклонение балки из-за точечной силы сильно локализовано. Отклонение является наибольшим в точке удара, а затем быстро уменьшается. Символический результат позволяет анализировать свойства результата, что невозможно при использовании числовых результатов.

Обратите внимание, что YSol является продуктом терминов. Термин с sin показывает, что реакция вибрирует колебательное поведение. Термин с exp показывает, что колебательное поведение быстро демпфируется экспоненциальным спадом по мере увеличения расстояния от точки удара.

Документация