Решение уравнений разностей с помощью Z-преобразования

Решите уравнения разностей, используя Z-преобразования в символьных математических Toolbox™ с этим рабочим процессом. Простые примеры Z-преобразования см. в разделе ztrans и iztrans.

Определение: Z-преобразование

Z-преобразование функции f (n) определяется как

$F (z)_{}^{} \frac{=∑n=0∞f}{(^{n}})$ zn.

Концепция: Использование символьных рабочих процессов

Символьные рабочие процессы содержат вычисления в натуральной символической форме, а не в числовой. Этот подход помогает понять свойства решения и использовать точные символьные значения. Числа подставляются вместо символьных переменных только в том случае, если требуется числовой результат или невозможно продолжить символьно. Дополнительные сведения см. в разделе Выбор числовой или символьной арифметики. Обычно этапы:

Объявить уравнения.
Решите уравнения.
Подстановочные значения.
Результаты графика.
Анализ результатов.

Рабочий процесс: Решение проблемы «кроличьего роста» с помощью Z-преобразования

Объявить уравнения

Можно использовать Z-преобразование для решения дифференциальных уравнений, таких как известная задача «Кроличий рост». Если пара кроликов созревает в один год, а затем каждый год производит другую пару кроликов, популяция кроликов p (n) в год n описывается этим уравнением различий.

p (n + 2) = p (n + 1) + p (n).

Объявить уравнение как выражение, предполагающее, что правая сторона 0. Поскольку n представляет годы, предположим, что n является положительным целым числом. Это предположение упрощает результаты.

syms p(n) z
assume(n>=0 & in(n,'integer'))
f = p(n+2) - p(n+1) - p(n)

f =
p(n + 2) - p(n + 1) - p(n)

Уравнения решения

Найдите Z-преобразование уравнения.

fZT = ztrans(f,n,z)

fZT =
z*p(0) - z*ztrans(p(n), n, z) - z*p(1) + z^2*ztrans(p(n), n, z) - ...
        z^2*p(0) - ztrans(p(n), n, z)

Функция solve решает только для символьных переменных. Поэтому использовать solve, первая замена ztrans(p(n),n,z) с переменными pZT.

syms pZT
fZT = subs(fZT,ztrans(p(n),n,z),pZT)

fZT =
z*p(0) - pZT - z*p(1) - pZT*z - z^2*p(0) + pZT*z^2

Решение для pZT.

pZT = solve(fZT,pZT)

pZT =
-(z*p(1) - z*p(0) + z^2*p(0))/(- z^2 + z + 1)

Вычислите p (n) путем вычисления обратного Z-преобразования pZT. Упростите результат.

pSol = iztrans(pZT,z,n);
pSol = simplify(pSol)

pSol =
2*(-1)^(n/2)*cos(n*(pi/2 + asinh(1/2)*1i))*p(1) + ...
                 (2^(2 - n)*5^(1/2)*(5^(1/2) + 1)^(n - 1)*(p(0)/2 - p(1)))/5 - ...
                 (2*2^(1 - n)*5^(1/2)*(1 - 5^(1/2))^(n - 1)*(p(0)/2 - p(1)))/5

Подстановочные значения

Чтобы нарисовать результат, сначала замените значения начальных условий. Давайте p(0) и p(1) быть 1 и 2соответственно.

pSol = subs(pSol,[p(0) p(1)],[1 2])

pSol =
4*(-1)^(n/2)*cos(n*(pi/2 + asinh(1/2)*1i)) - (3*2^(2 - n)*5^(1/2)* ...
    (5^(1/2) + 1)^(n - 1))/10 + (3*2^(1 - n)*5^(1/2)*(1 - 5^(1/2))^(n - 1))/5

Результаты графика

Показать рост популяции кроликов с течением времени путем построения графиков pSol.

nValues = 1:10;
pSolValues = subs(pSol,n,nValues);
pSolValues = double(pSolValues);
pSolValues = real(pSolValues);
stem(nValues,pSolValues)
title('Rabbit Population')
xlabel('Years (n)')
ylabel('Population p(n)')
grid on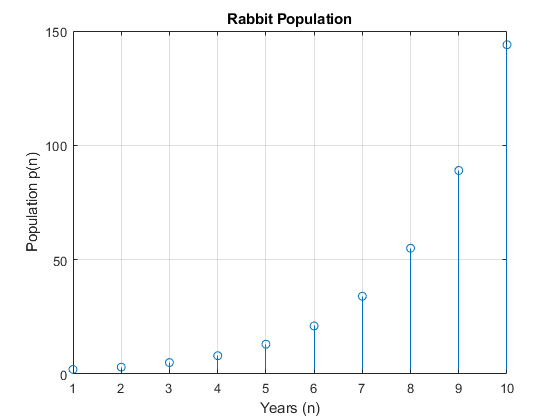

Анализ результатов

График показывает, что решение увеличивается экспоненциально. Однако, потому что решение pSol содержит много терминов, поиск терминов, создающих такое поведение, требует анализа.

Потому что все функции в pSol может быть выражено в терминах exp, переписать pSol кому exp. Упрощение результата с помощью simplify с 80 дополнительные этапы упрощения. Теперь вы можете анализировать pSol.

pSol = rewrite(pSol,'exp');
pSol = simplify(pSol,'Steps',80)

pSol =
(2*2^n)/(- 5^(1/2) - 1)^n - (3*5^(1/2)*(1/2 - 5^(1/2)/2)^n)/10 + ...
    (3*5^(1/2)*(5^(1/2)/2 + 1/2)^n)/10 - (3*(1/2 - 5^(1/2)/2)^n)/2 + ...
    (5^(1/2)/2 + 1/2)^n/2

Визуальный осмотр pSol. Обратите внимание, что pSol - сумма терминов. Каждый член - это отношение, которое может увеличиваться или уменьшаться как n увеличивается. Для каждого термина можно подтвердить эту гипотезу несколькими способами:

Проверьте, не установлен ли предел в n = Inf переходит к 0 или Inf с помощью limit.
Постройте график срока увеличения n и проверить поведение.
Вычислите значение при большом значении n.

Для простоты используйте третий подход. Рассчитайте условия в n = 100, а затем проверьте подход. Во-первых, найдите отдельные термины с помощью children, заменить n, и преобразовать в двойную.

pSolTerms = children(pSol);
pSolTermsDbl = subs(pSolTerms,n,100);
pSolTermsDbl = double(pSolTermsDbl)

pSolTermsDbl =
   1.0e+20 *
    0.0000   -0.0000    5.3134   -0.0000    3.9604

Результат показывает, что некоторые термины 0 в то время как другие термины имеют большую величину. Предположим, что члены большой величины производят экспоненциальное поведение. Приблизительный pSol с этими терминами.

idx = abs(pSolTermsDbl)>1; % use arbitrary cutoff
pApprox = pSolTerms(idx);
pApprox = sum(pApprox)

pApprox =
(3*5^(1/2)*(5^(1/2)/2 + 1/2)^n)/10 + (5^(1/2)/2 + 1/2)^n/2

Проверьте гипотезу, выведя на график ошибку аппроксимации между pSol и pApprox. Как и ожидалось, ошибка переходит к 0 как n увеличивается. Этот результат демонстрирует, как символичные вычисления помогают проанализировать проблему.

Perror = pSol - pApprox;
nValues = 1:30;
Perror = subs(Perror,n,nValues);
stem(nValues,Perror)
xlabel('Years (n)')
ylabel('Error (pSol - pApprox)')
title('Error in Approximation')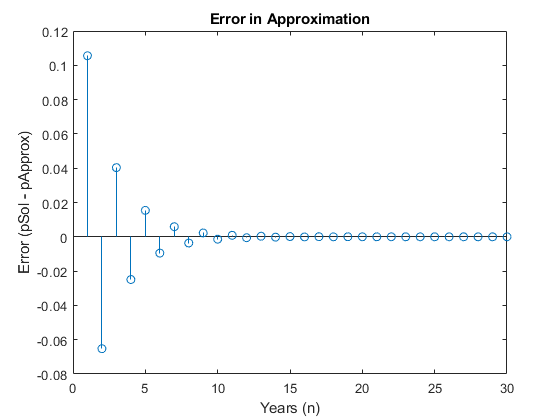

Ссылки

[1] Эндрюс, Л.С., Шивамогги, Б. К., Интегральные преобразования для инженеров и прикладных математиков, издательская компания Макмиллан, Нью-Йорк, 1986

[2] Crandall, R.E., Проекты в области научных вычислений, Springer-Verlag Publishers, Нью-Йорк, 1994

[3] Стрэнг, Г., Введение в прикладную математику, Уэлсли-Кембридж Пресс, Уэлсли, Массачусетс, 1986

Документация