Интеграция

Если f является символическим выражением, то

int(f)

пытается найти другое символическое выражение, F, так что diff(F) = f. То есть int(f) возвращает неопределенный интеграл или антипроизводный f (при условии, что он существует в закрытой форме). Аналогично дифференциации,

int(f,v)

использует символический объект v в качестве переменной интегрирования, а не переменной, определяемой symvar. Посмотреть, как int работает, глядя на эту таблицу.

Математическая операция	Команда MATLAB ®
$^{} \begin{array}{l} ∫xndx={log (x & ) , если n \\ \frac{=^{-}}{1xn} & + 1n + \end{array}$ 1в противном случае.	`int(x^n)` или `int(x^n,x)`
$_{}^{} ∫0π/2sin (2x) dx$ = 1	`int(sin(2x), 0, pi/2)` или `int(sin(2x), x, 0, pi/2)`
g = cos (при + b) $∫g (t) dt = sin (при$ + b )/a	`g = cos(a*t + b) int(g)` или `int(g, t)`
$_{∫J1} (z) dz_{=} -$ J0 (z)	`int(besselj(1, z))` или `int(besselj(1, z), z)`

В отличие от дифференциации, символическая интеграция является более сложной задачей. При вычислении интеграла может возникнуть ряд трудностей:

Противопроизводное, F, не может существовать в закрытой форме.
Противопроизводное может определять незнакомую функцию.
Антипроизводное может существовать, но программное обеспечение не может его найти.
Программное обеспечение может найти противопроизводное на более крупном компьютере, но на доступном компьютере не хватает времени или памяти.

Тем не менее, во многих случаях MATLAB может успешно выполнять символьную интеграцию. Например, создайте символьные переменные

syms a b theta x y n u z

Следующая таблица иллюстрирует интеграцию выражений, содержащих эти переменные.

f	int (f)
syms x n f = x^n;	int(f) ans = piecewise(n == -1, log(x), n ~= -1,... x^(n + 1)/(n + 1))
syms y f = y^(-1);	int(f) ans = log(y)
syms x n f = n^x;	int(f) ans = n^x/log(n)
syms a b theta f = sin(a*theta+b);	int(f) ans = -cos(b + a*theta)/a
syms u f = 1/(1+u^2);	int(f) ans = atan(u)
syms x f = exp(-x^2);	int(f) ans = (pi^(1/2)*erf(x))/2

В последнем примере: exp(-x^2), отсутствует формула для интеграла, включающего стандартные выражения исчисления, такие как тригонометрические и экспоненциальные функции. В этом случае MATLAB возвращает ответ с точки зрения функции ошибки erf.

Если MATLAB не может найти ответ на интеграл функции f, он просто возвращается int(f).

Возможна также определенная интеграция.

Определенный интеграл	Команда
$_{}^{} ∫abf (x)$ dx	`int(f, a, b)`
$_{}^{} ∫abf (v)$ dv	`int(f, v, a, b)`

Определенный интеграл

Команда

$_{}^{} ∫abf (x)$ dx

int(f, a, b)

$_{}^{} ∫abf (v)$ dv

int(f, v, a, b)

Вот несколько дополнительных примеров.

f	a, b	int (f, a, b)
syms x f = x^7;	a = 0; b = 1;	int(f, a, b) ans = 1/8
syms x f = 1/x;	a = 1; b = 2;	int(f, a, b) ans = log(2)
syms x f = log(x)*sqrt(x);	a = 0; b = 1;	int(f, a, b) ans = -4/9
syms x f = exp(-x^2);	a = 0; b = inf;	int(f, a, b) ans = pi^(1/2)/2
syms z f = besselj(1,z)^2;	a = 0; b = 1;	int(f, a, b) ans = hypergeom([3/2, 3/2],... [2, 5/2, 3], -1)/12

Для функции Бесселя (besselj) например, можно вычислить численное приближение к значению интеграла, используя double функция. Команды

syms z
a = int(besselj(1,z)^2,0,1)

вернуть

a =
hypergeom([3/2, 3/2], [2, 5/2, 3], -1)/12

и команды

a = double(a)

прибыль

a =
    0.0717

Интеграция с реальными параметрами

Одной из тонкостей, участвующих в символической интеграции, является «значение» различных параметров. Например, если a - любое положительное вещественное число, выражение

$e^{-^{}}$ ax2

- положительная, колоколообразная кривая, которая стремится к 0, так как x стремится к ±∞. Можно создать пример этой кривой для a = 1/2.

syms x
a = sym(1/2);
f = exp(-a*x^2);
fplot(f)

Figure contains an axes. The axes contains an object of type functionline.

Однако при попытке вычислить интеграл

$_{}^{}^{^{}} ∫−∞∞e−ax2dx$

без назначения значения, MATLAB предполагает, что a представляет комплексное число, и, следовательно, возвращает кусочный ответ, который зависит от аргумента a. Если вы заинтересованы только в случае, когда a является положительным вещественным числом, используйте assume для установки предположения на a:

syms a
assume(a > 0)

Теперь можно рассчитать предыдущий интеграл с помощью команд

syms x
f = exp(-a*x^2);
int(f, x, -inf, inf)

Это возвращает

ans =
pi^(1/2)/a^(1/2)

Интеграция со сложными параметрами

Расчет интеграла

$_{}^{} \frac{}{^{}^{∫−∞∞1a2+x2}} dx$

для комплексных значений a, введите

syms a x 
f = 1/(a^2 + x^2);
F = int(f, x, -inf, inf)

Использовать syms очистить все допущения по переменным. Дополнительные сведения о символьных переменных и допущениях для них см. в разделе Удаление символьных объектов и их предположений.

Предыдущие команды создают сложные выходные данные

F = 
(pi*signIm(1i/a))/a

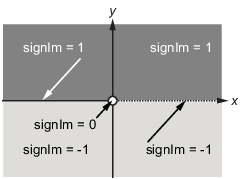
Функция signIm определяется как:

$signIm (z) \begin{array}{l} = & {1if Im (z) > 0 или Im (z ) = \\ 0 & и z \\ < & 00if z = \end{array}$ 0-1в противном случае.

Оценить F в a = 1 + i, введите

g = subs(F, 1 + i)

g = 
pi*(1/2 - 1i/2)

double(g)

ans =
   1.5708 - 1.5708i

Высокоточная численная интеграция с использованием арифметики переменной точности

Высокоточная цифровая интеграция реализована в vpaintegral функция символьного математического Toolbox™. vpaintegral использует арифметику переменной точности в отличие от MATLAB integral функция, использующая арифметику двойной точности.

Объединяться besseli(5,25*u).*exp(-u*25) с использованием обоих integral и vpaintegral. integral функция возвращает NaN и выдает предупреждение, пока vpaintegral возвращает правильный результат.

syms u
f = besseli(5,25*x).*exp(-x*25);
fun = @(u)besseli(5,25*u).*exp(-u*25);

usingIntegral = integral(fun, 0, 30)
usingVpaintegral = vpaintegral(f, 0, 30)

Warning: Infinite or Not-a-Number value encountered. 
usingIntegral =
   NaN

usingVpaintegral =
0.688424

Дополнительные сведения см. в разделе vpaintegral.

Документация

Интеграция

Интеграция с реальными параметрами

Интеграция со сложными параметрами

Высокоточная численная интеграция с использованием арифметики переменной точности

Документация по инструментам символьной математики

Поддержка