ldaModel

Латентная модель распределения Дирихле (LDA)

Описание

Скрытая модель распределения Дирихле (LDA) - это модель темы, которая обнаруживает основные темы в коллекции документов и выводит вероятности слов в темах. Если модель была подогнана с использованием модели мешка n-грамм, то программное обеспечение рассматривает n-грамм как отдельные слова.

Создание

Создание модели LDA с помощью fitlda функция.

Свойства

развернуть все

`NumTopics` - Количество тем
положительное целое число

Число тем в модели LDA, указанное как положительное целое число.

`TopicConcentration` - Тематическая концентрация
положительный скаляр

Концентрация тематики, заданная как положительный скаляр. Функция устанавливает концентрацию на тему как TopicConcentration/NumTopics. Дополнительные сведения см. в разделе Латентное распределение дирихле.

`WordConcentration` - Концентрация слов
`1` (по умолчанию) | неотрицательный скаляр

Концентрация слов, заданная как неотрицательный скаляр. Программное обеспечение устанавливает концентрацию на слово в WordConcentration/numWords, где numWords - словарный размер входных документов. Дополнительные сведения см. в разделе Латентное распределение дирихле.

`CorpusTopicProbabilities` - Тематические вероятности набора входных документов
вектор

Тематические вероятности набора входных документов, указанные как вектор. Вероятности темы корпуса модели LDA - это вероятности наблюдения за каждой темой во всем наборе данных, используемом для соответствия модели LDA. CorpusTopicProbabilities - вектор 1-by-K, где K - число тем. k-ый ввод CorpusTopicProbabilities соответствует вероятности наблюдения за темой k.

`DocumentTopicProbabilities` - Вероятность темы по входному документу
матрица

Вероятность темы по входному документу, заданная в виде матрицы. Вероятности темы документа модели LDA - это вероятности наблюдения за каждой темой в каждом документе, используемом для соответствия модели LDA. DocumentTopicProbabilities - матрица D-by-K, где D - количество документов, используемых для соответствия модели LDA, а K - количество тем. (d, k) -я запись DocumentTopicProbabilities соответствует вероятности наблюдения за темой k в документе d.

Если какие-либо темы имеют нулевую вероятность (CorpusTopicProbabilities содержит нули), затем соответствующие столбцы DocumentTopicProbabilities и TopicWordProbabilities являются нулями.

Порядок строк в DocumentTopicProbabilities соответствует порядку документов в данных обучения.

`TopicWordProbabilities` - Вероятности слов по темам
матрица

Вероятности слов для каждого раздела, указанные как матрица. Вероятности тематических слов модели LDA - это вероятности наблюдения за каждым словом в каждой теме модели LDA. TopicWordProbabilities является матрицей V-by-K, где V - число слов в Vocabulary и K - количество тем. (v, k) -я запись TopicWordProbabilities соответствует вероятности наблюдения слова v в теме k.

Порядок строк в TopicWordProbabilities соответствует порядку слов в Vocabulary.

`TopicOrder` - Порядок тематики
`'initial-fit-probability'` (по умолчанию) | `'unordered'`

Порядок тематики, указанный как одно из следующих:

'initial-fit-probability' - Сортировать темы по вероятностям темы корпуса начальной модели. Эти вероятности являются CorpusTopicProbabilities свойство начального ldaModel объект, возвращенный fitlda. resume функция не изменяет порядок тем результирующего ldaModel объекты.
'unordered' - Не заказывать темы.

`FitInfo` - Информация, записанная при установке модели LDA
структура

Информация, записанная при подборе модели LDA, заданная как структура со следующими полями:

TerminationCode - Состояние оптимизации при выходе
- 0 - достигнут предел итерации.
- 1 - Допуск по логарифмическому правдоподобию удовлетворен.
TerminationStatus - Объяснение возвращенного кода окончания
NumIterations - Количество выполненных итераций
NegativeLogLikelihood - Отрицательное логарифмическое правдоподобие для данных, переданных fitlda
Perplexity - Недоумение в отношении данных, переданных fitlda
Solver - имя используемого решателя;
History - Структура, хранящая историю оптимизации
StochasticInfo - Информация о структуре для стохастических решателей

Типы данных: struct

`Vocabulary` - Список слов в модели
строковый вектор

Список слов в модели, указанный как строковый вектор.

Типы данных: string

Функции объекта

`logp`	Документирование вероятностей и достоверности соответствия модели LDA
`predict`	Прогнозирование основных тем документов LDA
`resume`	Возобновить установку модели LDA
`topkwords`	Наиболее важные слова в сумке слов модели или темы LDA
`transform`	Преобразование документов в пространство нижних размеров
`wordcloud`	Создание таблицы облака слов из текста, модели мешка слов, модели мешка n граммов или модели LDA

Примеры

свернуть все

Подогнать модель LDA

Открыть сценарий в реальном времени

Чтобы воспроизвести результаты в этом примере, установите rng кому 'default'.

rng('default')

Загрузите данные примера. Файл sonnetsPreprocessed.txt содержит предварительно обработанные версии сонетов Шекспира. Файл содержит один сонет на строку со словами, разделенными пробелом. Извлечь текст из sonnetsPreprocessed.txtразделите текст на документы с новыми символами, а затем пометьте документы.

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создание модели сумки слов с помощью bagOfWords.

bag = bagOfWords(documents)

bag = 
  bagOfWords with properties:

          Counts: [154x3092 double]
      Vocabulary: [1x3092 string]
        NumWords: 3092
    NumDocuments: 154

Поместите модель LDA с четырьмя темами.

numTopics = 4;
mdl = fitlda(bag,numTopics)

Initial topic assignments sampled in 0.077325 seconds.
=====================================================================================
| Iteration  |  Time per  |  Relative  |  Training  |     Topic     |     Topic     |
|            | iteration  | change in  | perplexity | concentration | concentration |
|            | (seconds)  |   log(L)   |            |               |   iterations  |
=====================================================================================
|          0 |       0.36 |            |  1.215e+03 |         1.000 |             0 |
|          1 |       0.01 | 1.0482e-02 |  1.128e+03 |         1.000 |             0 |
|          2 |       0.01 | 1.7190e-03 |  1.115e+03 |         1.000 |             0 |
|          3 |       0.01 | 4.3796e-04 |  1.118e+03 |         1.000 |             0 |
|          4 |       0.01 | 9.4193e-04 |  1.111e+03 |         1.000 |             0 |
|          5 |       0.01 | 3.7079e-04 |  1.108e+03 |         1.000 |             0 |
|          6 |       0.01 | 9.5777e-05 |  1.107e+03 |         1.000 |             0 |
=====================================================================================

mdl = 
  ldaModel with properties:

                     NumTopics: 4
             WordConcentration: 1
            TopicConcentration: 1
      CorpusTopicProbabilities: [0.2500 0.2500 0.2500 0.2500]
    DocumentTopicProbabilities: [154x4 double]
        TopicWordProbabilities: [3092x4 double]
                    Vocabulary: [1x3092 string]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

Визуализация тем с помощью облаков слов.

figure
for topicIdx = 1:4
    subplot(2,2,topicIdx)
    wordcloud(mdl,topicIdx);
    title("Topic: " + topicIdx)
end

Figure contains objects of type wordcloud. The chart of type wordcloud has title Topic: 1. The chart of type wordcloud has title Topic: 2. The chart of type wordcloud has title Topic: 3. The chart of type wordcloud has title Topic: 4.

Слова с наибольшей вероятностью темы LDA

Открыть сценарий в реальном времени

Создайте таблицу слов с наибольшей вероятностью темы LDA.

Для воспроизведения результатов установите rng кому 'default'.

rng('default')

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создание модели сумки слов с помощью bagOfWords.

bag = bagOfWords(documents);

Поместите модель LDA с 20 темами. Для подавления подробных выходных данных установите 'Verbose' в 0.

numTopics = 20;
mdl = fitlda(bag,numTopics,'Verbose',0);

Найдите 20 лучших слов первой темы.

k = 20;
topicIdx = 1;
tbl = topkwords(mdl,k,topicIdx)

tbl=20×2 table
      Word        Score  
    ________    _________

    "eyes"        0.11155
    "beauty"      0.05777
    "hath"       0.055778
    "still"      0.049801
    "true"       0.043825
    "mine"       0.033865
    "find"       0.031873
    "black"      0.025897
    "look"       0.023905
    "tis"        0.023905
    "kind"       0.021913
    "seen"       0.021913
    "found"      0.017929
    "sin"        0.015937
    "three"      0.013945
    "golden"    0.0099608
      ⋮

Найдите 20 лучших слов первой темы и используйте обратное среднее масштабирование на баллах.

tbl = topkwords(mdl,k,topicIdx,'Scaling','inversemean')

tbl=20×2 table
      Word       Score  
    ________    ________

    "eyes"        1.2718
    "beauty"     0.59022
    "hath"        0.5692
    "still"      0.50269
    "true"       0.43719
    "mine"       0.32764
    "find"       0.32544
    "black"      0.25931
    "tis"        0.23755
    "look"       0.22519
    "kind"       0.21594
    "seen"       0.21594
    "found"      0.17326
    "sin"        0.15223
    "three"      0.13143
    "golden"    0.090698
      ⋮

Создайте облако слов, используя масштабированные оценки в качестве данных размера.

figure
wordcloud(tbl.Word,tbl.Score);

Figure contains an object of type wordcloud.

Тема документа Вероятности модели LDA

Открыть сценарий в реальном времени

Получение вероятностей тематики документа (также известных как смеси тематик) документов, используемых для соответствия модели LDA.

Для воспроизведения результатов установите rng кому 'default'.

rng('default')

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создание модели сумки слов с помощью bagOfWords.

bag = bagOfWords(documents);

Поместите модель LDA с 20 темами. Для подавления подробных выходных данных установите 'Verbose' в 0.

numTopics = 20;
mdl = fitlda(bag,numTopics,'Verbose',0)

mdl = 
  ldaModel with properties:

                     NumTopics: 20
             WordConcentration: 1
            TopicConcentration: 5
      CorpusTopicProbabilities: [1x20 double]
    DocumentTopicProbabilities: [154x20 double]
        TopicWordProbabilities: [3092x20 double]
                    Vocabulary: [1x3092 string]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

Просмотр вероятностей темы первого документа в данных обучения.

topicMixtures = mdl.DocumentTopicProbabilities;
figure
bar(topicMixtures(1,:))
title("Document 1 Topic Probabilities")
xlabel("Topic Index")
ylabel("Probability")

Figure contains an axes. The axes with title Document 1 Topic Probabilities contains an object of type bar.

Прогнозирование основных тем документов LDA

Открыть сценарий в реальном времени

Чтобы воспроизвести результаты в этом примере, установите rng кому 'default'.

rng('default')

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создание модели сумки слов с помощью bagOfWords.

bag = bagOfWords(documents)

bag = 
  bagOfWords with properties:

          Counts: [154x3092 double]
      Vocabulary: [1x3092 string]
        NumWords: 3092
    NumDocuments: 154

Поместите модель LDA с 20 темами.

numTopics = 20;
mdl = fitlda(bag,numTopics)

Initial topic assignments sampled in 0.029643 seconds.
=====================================================================================
| Iteration  |  Time per  |  Relative  |  Training  |     Topic     |     Topic     |
|            | iteration  | change in  | perplexity | concentration | concentration |
|            | (seconds)  |   log(L)   |            |               |   iterations  |
=====================================================================================
|          0 |       0.39 |            |  1.159e+03 |         5.000 |             0 |
|          1 |       0.13 | 5.4884e-02 |  8.028e+02 |         5.000 |             0 |
|          2 |       0.11 | 4.7400e-03 |  7.778e+02 |         5.000 |             0 |
|          3 |       0.11 | 3.4597e-03 |  7.602e+02 |         5.000 |             0 |
|          4 |       0.14 | 3.4662e-03 |  7.430e+02 |         5.000 |             0 |
|          5 |       0.11 | 2.9259e-03 |  7.288e+02 |         5.000 |             0 |
|          6 |       0.14 | 6.4180e-05 |  7.291e+02 |         5.000 |             0 |
=====================================================================================

mdl = 
  ldaModel with properties:

                     NumTopics: 20
             WordConcentration: 1
            TopicConcentration: 5
      CorpusTopicProbabilities: [1x20 double]
    DocumentTopicProbabilities: [154x20 double]
        TopicWordProbabilities: [3092x20 double]
                    Vocabulary: [1x3092 string]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

Прогнозирование основных тем для массива новых документов.

newDocuments = tokenizedDocument([
    "what's in a name? a rose by any other name would smell as sweet."
    "if music be the food of love, play on."]);
topicIdx = predict(mdl,newDocuments)

topicIdx = 2×1

    19
     8

Визуализация прогнозируемых тем с помощью облаков слов.

figure
subplot(1,2,1)
wordcloud(mdl,topicIdx(1));
title("Topic " + topicIdx(1))
subplot(1,2,2)
wordcloud(mdl,topicIdx(2));
title("Topic " + topicIdx(2))

Figure contains objects of type wordcloud. The chart of type wordcloud has title Topic 19. The chart of type wordcloud has title Topic 8.

Подробнее

развернуть все

Латентное распределение Дирихле

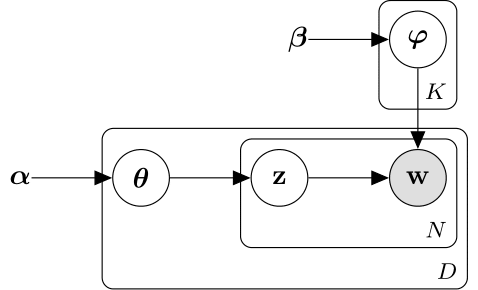
Скрытая модель распределения Дирихле (LDA) - это модель темы документа, которая обнаруживает основные темы в коллекции документов и выводит вероятности слов в темах. LDA моделирует совокупность D документов в качестве тематических смесей $_{}_{}$ θ1,...,θD, по K темам, характеризующимся векторами вероятностей слов $_{}_{}$ φ1,...,φK. Модель предполагает, что $_{} смеси$ тем θ1,...,θD, а $_{} темы_{}$ φ1,...,φK следовать распределению Дирихле с параметрами концентрации α и β соответственно.

Тематические смеси $_{}_{}$ θ1,...,θD являются вероятностными векторами длины K, где K - число тем. ${Запись}_{}$ startdi представляет собой вероятность появления темы i в dth-м документе. Тематические смеси соответствуют строкам DocumentTopicProbabilities имущества ldaModel объект.

Темами $_{}_{}$ φ1,...,φK являются вероятностные векторы длины V, где V - количество слов в лексике. ${Запись}_{}$ фiv соответствует вероятности появления v-го слова словаря в i-ой теме. Темы $_{}_{}$ φ1,...,φK соответствующие столбцам TopicWordProbabilities имущества ldaModel объект.

Учитывая темы $_{}_{}$ φ1,...,φK и Dirichlet, $предшествующие$ α по смесям тем, LDA предполагает следующий генеративный процесс для документа:

Возьмем образец тематической смеси, (( $α$ )). Случайная величина start- вектор вероятности длины K, где K - число тем.
Для каждого слова в документе:
1. Пример индекса тематики $z ~ Категориальный$ (start). Случайная величина z - целое число от 1 до K, где K - число тем.
2. Пример слова $w ~ {Категориальный}_{} ($ фз). Случайная величина w - целое число от 1 до V, где V - количество слов в лексике, и представляет соответствующее слово в лексике.

При этом генеративном процессе совместное распределение документа со словами $_{}_{}$ w1,...,wN, с тематической $смесью,$ и с тематическими ${индексами}_{}_{}$ z1,...,zN задается

$p (start, z, w 'α, start) = p_{(}^{} start' α)_{} \prodn=1Np_{(}_{} zn$ '

где N - количество слов в документе. Суммирование совместного распределения по оси z, а затем интегрирование по $оси$ , дает предельное распределение документа w:

$p (w 'α, start \underset{}{)} =\intθp (_{λ' α)}^{} \underset{_{}}{}_{} ∏n=1N∑znp (_{} zn_{}$ '

Следующая диаграмма иллюстрирует модель LDA как вероятностную графическую модель. Закрашенные узлы - наблюдаемые переменные, неокрашенные - скрытые переменные, узлы без контуров - параметры модели. Стрелки выделяют зависимости между случайными величинами и табличками указывают повторяющиеся узлы.

Распределение Дирихле

Распределение Дирихле - непрерывное обобщение полиномиального распределения. Учитывая число категорий $K≥2$ и параметр концентрации $α$ , где $α$ - вектор положительных реалов длины K, функция плотности вероятности распределения Дирихле задаётся

$p (θ ∣α) \frac{}{=1B}_{(α)}^{}_{}^{{∏i=1K}_{}}$ θiαi−1,

где B обозначает многомерную бета-функцию, заданную

$B (α) \frac{_{}^{} {=∏i=1KΓ}_{} (}{αi)_{Γ}^{(}_{}}$ ∑i=1Kαi).

Частным случаем распределения Дирихле является симметричное распределение Дирихле. Симметричное распределение Дирихле характеризуется параметром концентрации $α$ , где все элементы $α$ одинаковы.

См. также

Темы

Представлен в R2017b

Документация

ldaModel

Описание

Создание

Свойства

`NumTopics` - Количество тем
положительное целое число

`TopicConcentration` - Тематическая концентрация
положительный скаляр

`WordConcentration` - Концентрация слов
`1` (по умолчанию) | неотрицательный скаляр

`CorpusTopicProbabilities` - Тематические вероятности набора входных документов
вектор

`DocumentTopicProbabilities` - Вероятность темы по входному документу
матрица

`TopicWordProbabilities` - Вероятности слов по темам
матрица

`TopicOrder` - Порядок тематики
`'initial-fit-probability'` (по умолчанию) | `'unordered'`

`FitInfo` - Информация, записанная при установке модели LDA
структура

`Vocabulary` - Список слов в модели
строковый вектор

Функции объекта

Примеры

Подогнать модель LDA

Слова с наибольшей вероятностью темы LDA

Тема документа Вероятности модели LDA

Прогнозирование основных тем документов LDA

Подробнее

Латентное распределение Дирихле

Распределение Дирихле

См. также

Темы

Документация по инструментам для анализа текста

Поддержка

Документация

ldaModel

Описание

Создание

Свойства

NumTopics - Количество тем положительное целое число

TopicConcentration - Тематическая концентрация положительный скаляр

WordConcentration - Концентрация слов 1 (по умолчанию) | неотрицательный скаляр

CorpusTopicProbabilities - Тематические вероятности набора входных документов вектор

DocumentTopicProbabilities - Вероятность темы по входному документу матрица

TopicWordProbabilities - Вероятности слов по темам матрица

TopicOrder - Порядок тематики 'initial-fit-probability' (по умолчанию) | 'unordered'

FitInfo - Информация, записанная при установке модели LDA структура

Vocabulary - Список слов в модели строковый вектор

Функции объекта

Примеры

Подогнать модель LDA

Слова с наибольшей вероятностью темы LDA

Тема документа Вероятности модели LDA

Прогнозирование основных тем документов LDA

Подробнее

Латентное распределение Дирихле

Распределение Дирихле

См. также

Темы

Документация по инструментам для анализа текста

Поддержка

`NumTopics` - Количество тем
положительное целое число

`TopicConcentration` - Тематическая концентрация
положительный скаляр

`WordConcentration` - Концентрация слов
`1` (по умолчанию) | неотрицательный скаляр

`CorpusTopicProbabilities` - Тематические вероятности набора входных документов
вектор

`DocumentTopicProbabilities` - Вероятность темы по входному документу
матрица

`TopicWordProbabilities` - Вероятности слов по темам
матрица

`TopicOrder` - Порядок тематики
`'initial-fit-probability'` (по умолчанию) | `'unordered'`

`FitInfo` - Информация, записанная при установке модели LDA
структура

`Vocabulary` - Список слов в модели
строковый вектор