В этом разделе демонстрируются особенности многомерного деноизирования, предоставляемые программным обеспечением Wavelet Toolbox™. Панель инструментов включает wmulden функция и приложение Wavelet Analyzer. Этот раздел также описывает методы командной строки и приложения и включает информацию о передаче информации о сигнале и параметрах между диском и приложением.
Эта многомерная задача денонсации вейвлет имеет дело с моделями формы X (t) = F (t) + e (t), где наблюдение X является p-мерным, F является детерминированным сигналом, подлежащим восстановлению, и e является пространственно коррелированным шумовым сигналом. Этот вид модели хорошо подходит для ситуаций, для которых такой аддитивный пространственно коррелированный шум является реалистичным.
В этом примере используются шумные тестовые сигналы. В этом разделе вы
Загрузите многомерный сигнал.
Отображение исходных и наблюдаемых сигналов.
Удалите шум простым многомерным порогом после изменения базиса.
Отображение исходного и деноизированного сигналов.
Улучшите полученный результат, сохранив меньше основных компонентов.
Отображение количества сохраненных основных компонентов.
Отображение матрицы ковариации расчетного шума.
Загрузите многомерный сигнал, введя в подсказке MATLAB ® следующее:
load ex4mwden whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
covar | 4x4 | 128 | double array |
x | 1024x4 | 32768 | double array |
x_orig | 1024x4 | 32768 | double array |
Как правило, только матрица данных x доступен. Здесь мы также имеем истинную матрицу ковариации шума (covar) и исходные сигналы (x_orig). Эти сигналы являются шумными вариантами простых комбинаций двух исходных сигналов. Первый - «Блоки», который является нерегулярным, а второй - «Sine», который является регулярным, за исключением приблизительно 750-го времени. Два других сигнала являются суммой и разностью двух исходных сигналов. Многомерный гауссовский белый шум, демонстрирующий сильную пространственную корреляцию, добавляется к полученным четырем сигналам, что приводит к наблюдаемым данным, хранящимся в x.
Отображение исходных и наблюдаемых сигналов путем ввода
kp = 0;
for i = 1:4
subplot(4,2,kp+1), plot(x_orig(:,i)); axis tight;
title(['Original signal ',num2str(i)])
subplot(4,2,kp+2), plot(x(:,i)); axis tight;
title(['Observed signal ',num2str(i)])
kp = kp + 2;
end
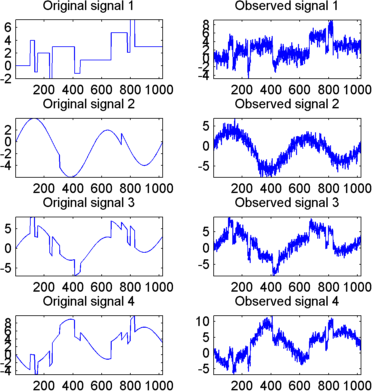
Истинная матрица ковариации шума задается
covar
covar =
1.0000 0.8000 0.6000 0.7000
0.8000 1.0000 0.5000 0.6000
0.6000 0.5000 1.0000 0.7000
0.7000 0.6000 0.7000 1.0000
Устраните шум простым многомерным порогом.
Стратегия деноизирования объединяет одномерное вейвлет-деноизирование в основе, где оцененная матрица ковариации шума диагональна, с нецентрированным анализом основных компонентов (PCA) на аппроксимациях в вейвлет-области или с конечным PCA.
Сначала выполните одномерное обесценение, набрав следующие значения для установки параметров обесценения:
level = 5; wname = 'sym4'; tptr = 'sqtwolog'; sorh = 's';
Затем установите параметры PCA, сохранив все основные компоненты:
npc_app = 4; npc_fin = 4;
Наконец, выполните многомерное отрицание путем ввода
x_den = wmulden(x, level, wname, npc_app, npc_fin, tptr, sorh);
Отображение исходных и обозначенных сигналов путем ввода
kp = 0;
for i = 1:4
subplot(4,3,kp+1), plot(x_orig(:,i));
set(gca,'xtick',[]); axis tight;
title(['Original signal ',num2str(i)])
subplot(4,3,kp+2), plot(x(:,i)); set(gca,'xtick',[]);
axis tight;
title(['Observed signal ',num2str(i)])
subplot(4,3,kp+3), plot(x_den(:,i)); set(gca,'xtick',[]);
axis tight;
title(['denoised signal ',num2str(i)])
kp = kp + 3;
end
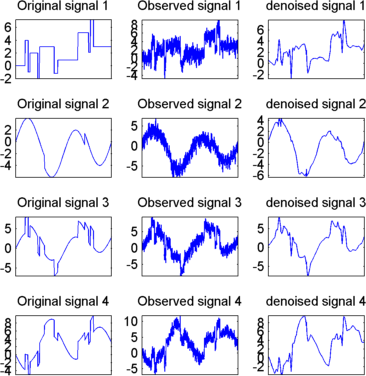
Улучшите первый результат, сохранив меньше главных компонентов.
Результаты удовлетворительные. Фокусируясь на двух первых сигналах, заметьте, что они правильно восстановлены, но результат может быть улучшен за счет использования преимуществ взаимосвязей между сигналами, приводящих к дополнительному деноизирующему эффекту.
Чтобы автоматически выбрать количество сохраненных основных компонентов по правилу Кайзера (которое удерживает компоненты, связанные с собственными значениями, превышающими среднее значение всех собственных значений), введите
npc_app = 'kais'; npc_fin = 'kais';
Снова выполните многомерную денуа, введя
[x_den, npc, nestco] = wmulden(x, level, wname, npc_app, ...
npc_fin, tptr, sorh);
Отображение количества сохраненных основных компонентов.
Второй выходной аргумент дает количество сохраненных главных компонентов для PCA для аппроксимаций и для конечного PCA.
npc
npc =
2 2
Как и ожидалось, поскольку сигналы представляют собой комбинации двух начальных, правило Кайзера автоматически обнаруживает, что интерес представляют только две основные компоненты.
Отображение матрицы ковариации расчетного шума.
Третий выходной аргумент содержит матрицу ковариации оцененного шума:
nestco
nestco =
1.0784 0.8333 0.6878 0.8141
0.8333 1.0025 0.5275 0.6814
0.6878 0.5275 1.0501 0.7734
0.8141 0.6814 0.7734 1.0967
Как вы можете видеть, сравнивая с истинным матричным коваром, приведенным ранее, оценка является удовлетворительной.
Отображение исходных и окончательных обозначенных сигналов путем ввода
kp = 0;
for i = 1:4
subplot(4,3,kp+1), plot(x_orig(:,i));
set(gca,'xtick',[]); axis tight;
title(['Original signal ',num2str(i)]); set(gca,'xtick',[]);
axis tight;
subplot(4,3,kp+2), plot(x(:,i)); set(gca,'xtick',[]);
axis tight;
title(['Observed signal ',num2str(i)])
subplot(4,3,kp+3), plot(x_den(:,i)); set(gca,'xtick',[]);
axis tight;
title(['denoised signal ',num2str(i)])
kp = kp + 3;
end
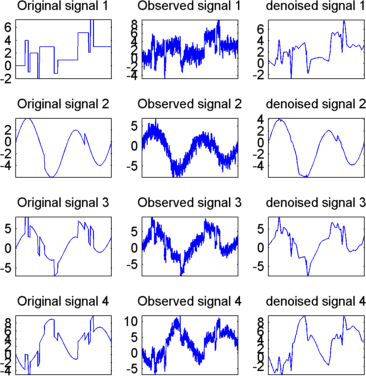
Результаты лучше, чем полученные ранее. Первый сигнал, который является нерегулярным, все еще правильно восстанавливается, в то время как второй сигнал, который является более регулярным, после этой второй ступени PCA денонсируется лучше.
В этом разделе рассматривается стратегия подавления многомерных сигналов с помощью приложения Wavelet Analyzer.
Запустите многомерный инструмент Denoising, предварительно открыв приложение Wavelet Analyzer. Тип waveletAnalyzer в командной строке.
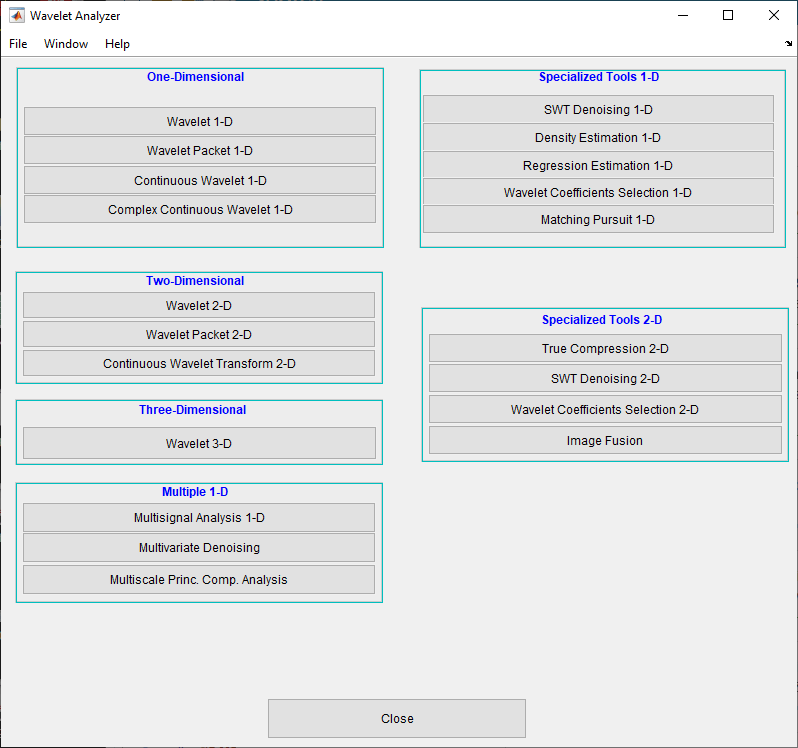
Щелкните Многомерный Деноизинг, чтобы открыть раздел Многомерный Деноизинг в приложении.
Загрузить данные.
В командной строке MATLAB введите
load ex4mwden
x переменная. Нажмите кнопку OK, чтобы импортировать шумный многомерный сигнал. Сигнал представляет собой матрицу, содержащую четыре столбца, где каждый столбец является сигналом, подлежащим деноузированию.
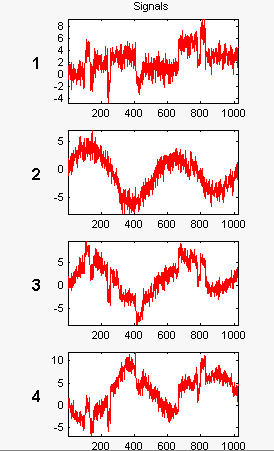
Эти сигналы являются шумными версиями из простых комбинаций двух исходных сигналов. Первый является «блоками», которые являются нерегулярными, а второй - «Sine», который является регулярным, за исключением приблизительно времени 750. Два других сигнала представляют собой сумму и разность между исходными сигналами. Многомерный гауссовский белый шум, проявляющий сильную пространственную корреляцию, добавляется к результирующим четырем сигналам.
Следующий пример иллюстрирует два различных аспекта предлагаемого способа деноизирования. Во-первых, выполнить удобное изменение базиса, чтобы справиться с пространственной корреляцией и денузой в новом базисе. Затем используйте PCA, чтобы воспользоваться соотношениями между сигналами, что приводит к дополнительному денойзирующему эффекту.
Выполните вейвлет-декомпозицию и диагонализацию матрицы ковариации шума.
Используйте отображаемые значения по умолчанию для вейвлета, режима расширения DWT и уровня разложения, а затем щелкните Разложить (Decompose) и Диагонализировать (Diagonalize). Инструмент отображает вейвлет-аппроксимацию и коэффициенты детализации разложения каждого сигнала в исходном базисе.
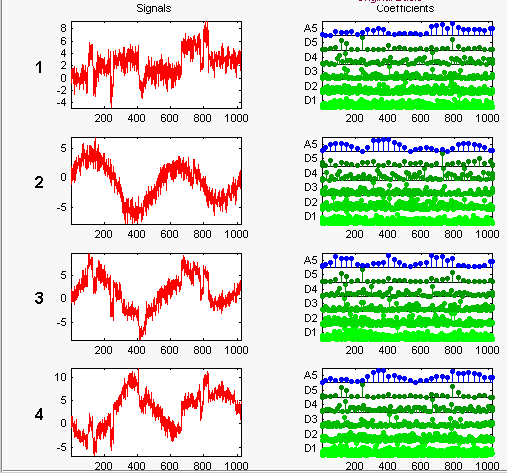
Для отображения сигналов и их коэффициентов в адаптированном к помехам базисе выберите Noise Adapted Basis.
Чтобы просмотреть дополнительные сведения об этом новом базисе, нажмите кнопку Дополнительно на адаптированном базисе шума. Новый рисунок отображает матрицу оценки ковариации надежного шума и соответствующие собственные векторы и собственные значения.
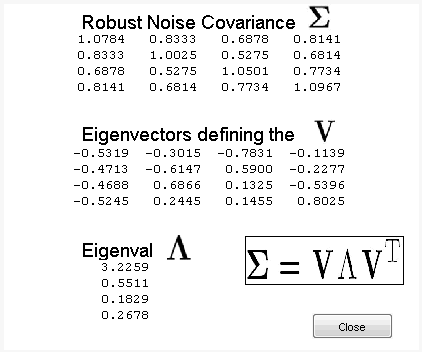
Собственные векторы определяют изменение базиса, а собственные значения являются дисперсиями некоррелированных шумов в новом базисе.
Предложенный ниже способ многомерного деноизирования интересен, если матрица ковариации шума далека от диагональной, проявляющей пространственную корреляцию, что в данном примере имеет место.
обличить многомерный сигнал.
Имеется ряд вариантов для точной настройки алгоритма деноизирования. Однако мы будем использовать значения по умолчанию: мягкое пороговое значение фиксированной формы, масштабированную модель белого шума и предлагаемые количества сохраненных основных компонентов. В этом случае значения по умолчанию для PCA приводят к сохранению всех компонентов.
Выберите Исходный базис (Original Basis), чтобы вернуться к исходному базису, а затем щелкните Деноиза (Denoise).
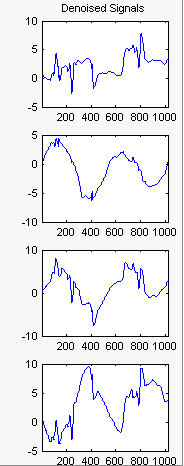
Результаты удовлетворительные. Оба первых сигнала правильно восстановлены, но они могут быть улучшены за счет получения дополнительной информации о главных компонентах. Щелкните Дополнительно (More) на вкладке Основные компоненты (Principal Components).
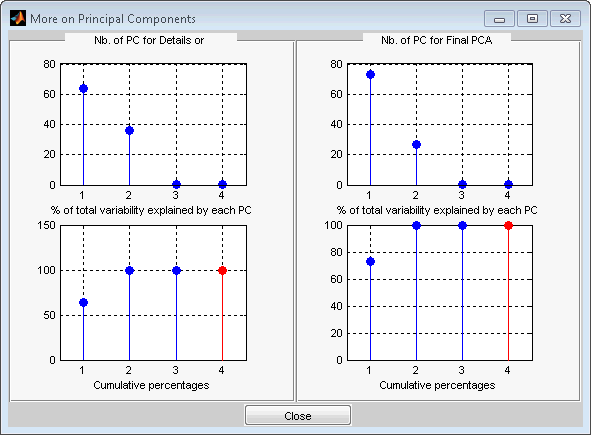
На новом рисунке отображается информация для выбора количества компонентов, сохраняемых для PCA аппроксимаций и для окончательного PCA после возврата к исходной основе. Можно просмотреть процент изменчивости, объясняемый каждым основным компонентом и соответствующим кумулятивным графиком. Здесь очевидно, что интерес представляют только два основных компонента.
Закройте окно Дополнительные сведения о главных компонентах. Выбрать 2 как Nb. ПК для APP. Выбрать 2 как Nb. PC для окончательного PCA, а затем нажмите denoise.
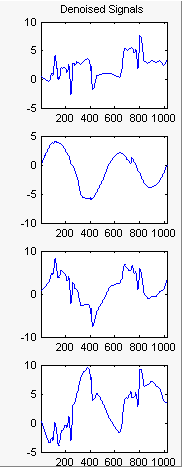
Результаты лучше, чем полученные ранее. Первый сигнал, который является нерегулярным, все еще правильно восстановлен. Второй сигнал, который является более регулярным, после этой второй ступени PCA денонсируется лучше. Дополнительную информацию можно получить, щелкнув Остатки (Residuals).
Инструмент позволяет сохранять запрещенные сигналы на диск, создавая MAT-файл в текущей папке с выбранным именем.
Для сохранения сигнала, обозначенного в предыдущем разделе,
Выберите File > Save denoised Signals (Файл).
Выберите «Save denoised Signals and Parameters» (Сохранить сигналы и параметры, денозированные). Появится диалоговое окно, в котором можно указать папку и имя файла для хранения сигнала.
Введите имя s_ex4mwden и нажмите кнопку ОК, чтобы сохранить данные.
Загрузите переменные в рабочую область:
load s_ex4mwdent whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
DEN_Params | 1x1 | 430 | struct array |
PCA_Params | 1x1 | 1536 | struct array |
x | 1024x4 | 32768 | struct array |
Денонсированные сигналы находятся в матрице x. Параметры (PCA_Params и DEN_Params) двухстадийного процесса обессоливания также доступны.
PCA_Params изменения базиса и параметров РСА:
PCA_Params
PCA_Params =
NEST: {[4x4 double] [4x1 double] [4x4 double]}
APP: {[4x4 double] [4x1 double] [2]}
FIN: {[4x4 double] [4x1 double] [2]}
PCA_Params.NEST{1} содержит перемену базисной матрицы. PCA_Params.NEST{2} содержит собственные значения, и PCA_Params.NEST{3} - оценка ковариационной матрицы шума.
PCA_Params.APP{1} содержит матрицу изменения базиса, PCA_Params.APP{2} содержит собственные значения, и PCA_Params.APP{3} - количество сохраненных главных компонентов для аппроксимаций.
Та же структура используется для PCA_Params.FIN для окончательного PCA.
DEN_Params - деноизлучающие параметры в диагональной основе:
DEN_Params
DEN_Params =
thrVAL: [4.8445 2.0024 1.1536 1.3957 0]
thrMETH: 'sqtwolog'
thrTYPE: 's'
Пороговые значения кодируются в thrVAL. Для j от 1 кому 5, thrVAL(j) содержит значение, используемое для порогового значения коэффициентов детализации на уровне j. Метод пороговой обработки задается thrMETH и пороговый режим задается thrTYPE.