Реализация алгоритма распространения убеждений основана на алгоритме декодирования, представленном в [2]. Для переданного кодового слова с кодировкой LDPC, c, где $$c=(c_0,c_1,\mathrm{...},c_{n-1})$$, входом для декодера LDPC является значение отношения логарифмической правдоподобности (LLR) $$L(c_i)=\log \left(\frac{\mathrm{Pr}(c_i=0|\text{channel output for }{c}_i)}{\mathrm{Pr}(c_i=1|\text{ выход для }{c}_i)}\right)$$.

В каждой итерации ключевые компоненты алгоритма обновляются на основе этих уравнений:

$$L(r_{ji})=2\text{atanh}\left({\displaystyle \prod _{i^{\prime }\in V_j\backslash i}\tanh \left(\frac{1}{2}L(q_{i^{\prime }j})\right)}\right)$$,

$$L(q_{ij})=L(c_i)+{\displaystyle \sum _{j^{\prime }\in C_i\backslash j}L(r_{j^{\prime }i})}$$, инициализированный как $$L(q_{ij})=L(c_i)$$ перед первой итерацией, и

$$L(Q_i)=L(c_i)+{\displaystyle \sum _{j^{\prime }\in C_i}L(r_{j^{\prime }i})}$$.

В конце каждой итерации, $$L(Q_i)$$ является обновленной оценкой значения LLR для переданного бита $$c_i$$. Значение $$L(Q_i)$$ - выходы мягкого решения для $$c_i$$. Если $$L(Q_i)<0$$, выход жесткого решения для $$c_i$$ равен 1. В противном случае выводится значение 0.

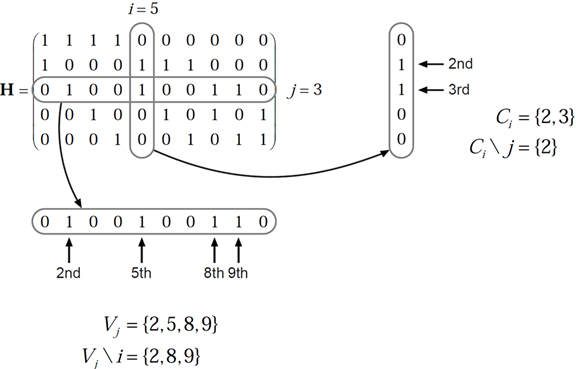
Наборы индексов $$C_i\backslash j$$ и $$V_j\backslash i$$ основаны на матрице проверки четности (PCM). Наборы индексов $$C_i$$ и $$V_j$$ соответствуют всем ненулевым элементам в столбцах i и j строках PCM, соответственно.

Этот рисунок подсвечивает расчет этих наборов индексов в заданном PCM для i = 5 и j = 3.

Чтобы избежать бесконечных чисел в уравнениях алгоритма, atanh (1) и atanh (-1) устанавливаются в 19.07 и -19.07 соответственно. Из-за конечной точности MATLAB^® возвращает 1 для танха (19.07) и -1 для танха (-19.07).

Когда аргумент пары "имя-значение" 'Termination' установлено в 'max'декодирование заканчивается после maxNumIter количество итераций. Когда 'Termination' установлено в 'early'декодирование заканчивается, когда выполняются все проверки четности ($$H{c}^{\text{T}}=0$$) или после maxNumIter количество итераций.

Реализация алгоритма распространения многоуровневых убеждений основана на алгоритме декодирования, представленном в [3], раздел II.A. Цикл декодирования итерирует над подмножествами строк (слоев) PCM. Для каждой строки, m, в слое и каждом битовом индексе, j, реализация обновляет ключевые компоненты алгоритма на основе этих уравнений:

(1) $$L(q_{mj})=L(q_j)-R_{mj}$$,

(2) $$A_{mj}={\displaystyle \sum _{\begin{array}{c}n \in N\left(m\right)\\ n\ne j\end{array}}\text{ψ}(L(q_{mn}))}$$,

(3) $$s_{mj}={\displaystyle \prod _{\begin{array}{c}n \in N\left(m\right)\\ n\ne j\end{array}}\text{знак}(L(q_{mn}))}$$,

(4) $$R_{mj}=-s_{mj}\text{ψ}(A_{mj})$$, и

(5) $$L(q_j)=L(q_{mj})+R_{mj}$$.

Для каждого слоя уравнение декодирования (5) работает на объединенном входе, полученном из текущих входов LLR $$L(q_{mj})$$ и обновляется предыдущий слой $$R_{mj}$$.

Поскольку в слое обновляется только подмножество узлов, алгоритм распространения многослойных убеждений быстрее по сравнению с алгоритмом распространения убеждений. Чтобы достичь той же частоты ошибок, что и при декодировании распространения убеждений, используйте половину количества итераций декодирования при использовании алгоритма распространения многоуровневых убеждений.

Реализация нормированного алгоритма декодирования min-sum следует многоуровневому алгоритму распространения убеждений с уравнением (2), замененным на

$$A_{mj}=\underset{\begin{array}{c}n \in N\left(m\right)\\ n\ne j\end{array}}{\min }(\left|L(q_{mn}) \right|\cdot \alpha )$$,

где α находится в области значений (0, 1] и является масштабным коэффициентом, заданным ScalingFactor. Это уравнение является адаптацией уравнения (4), представленного в [4].

Реализация алгоритма смещения min-sum следует многоуровневому алгоритму распространения убеждений с уравнением (2), замененным на

$$A_{mj} = \max (\underset{\begin{array}{c}n \in N\left(m\right)\\ n\ne j\end{array}}{\min } (\left|L\left(q_{mn}\right)\right|- \beta ), 0)$$,

где β ≥ 0 и является смещением, заданным Offset. Это уравнение является адаптацией уравнения (5), представленного в [4].