Exponenta Banner

Zonal Harmonic Gravity Model

Вычислите зональное гармоническое представление планетарной гравитации

развернуть все на странице
  • Библиотека:

  • Aerospace Blockset/Окружающая среда/Гравитация

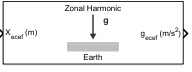
  • Zonal Harmonic Gravity Model block

Описание

Блок Zonal Harmonic Gravity Model вычисляет зональное гармоническое представление планетарного веса в определенном месте на основе гравитационного потенциала планеты. Этот блок обеспечивает удобный способ описания гравитационного поля планеты вне ее поверхности.

По умолчанию блок использует зональный коэффициент четвертого порядка для Земли, чтобы вычислить зональную гармоническую силу тяжести. Это также позволяет вам задать второй или третий зональный коэффициент.

Для получения информации о значениях планетарных параметров для каждой планеты в реализации блока, смотрите Algorithms.

Порты

Вход

расширить все

Ориентированные на планету фиксированные координаты, заданные как матрица m-на-3, от центра планеты в выбранных модулях измерения длины. Если Planet model имеет значение Earth, эта матрица содержит координаты ECEF.

Типы данных: double

Выход

расширить все

Значения гравитации, возвращенные как m-на-3 массив, в осях X, Y и Z центрированных планет фиксированных координат, в выбранных модулях измерения длины в секунду в квадрате.

Типы данных: double

Параметры

расширить все

Входные модули, заданные как:

Модули

Положение

Экваториальный радиус

Гравитационный параметр

Metric (MKS)

Метры

Метры

Метры в кубе в секунду за секунду

English

Ноги

Ноги

Футы в кубе в секунду за секунду

Программное использование

Параметры блоков: units
Тип: Вектор символов
Значения: 'Metric (MKS)' | 'English'
По умолчанию: 'Metric (MKS)'

Степень гармонической модели, заданная как.

  • 2 - Вторая степень, J2. Самый значительный или самый большой сферический гармонический термин, который учитывает облатность планеты.

  • 3 - Третья степень, J3.

  • 4 - Четвертая степень, J4 (по умолчанию).

Программное использование

Параметры блоков: degree
Тип: Вектор символов
Значения: '2' | '3' | '4'
По умолчанию: '4'

Поведение входа вне области допустимого, заданное как:

ЗначениеОписание

None

Никаких действий.

Warning

Предупреждение в Diagnostic Viewer, симуляция модели продолжается.

Error

MATLAB® возвращает исключение, симуляция модели останавливается.

Программное использование

Параметры блоков: action
Тип: Вектор символов
Значения: 'None' | 'Warning' | 'Error'
По умолчанию: 'Warning'

Планетарная модель, заданная как Mercury, Venus, Earth, Moon, Mars, Jupiter, Saturn, Uranus, Neptune, или Custom.

Выбор Custom позволяет вам задать свою собственную планетарную модель.

  • Выбор Mercury, Venus, Moon, Uranus, или Neptune ограничивает степень 2.

  • Выбор Mars ограничивает степень 3.

Зависимости

Выбор Custom включает параметры Equatorial radius, Gravitational parameter и J values rate.

Программное использование

Параметры блоков: ptype
Тип: Вектор символов
Значения: 'Mercury' | 'Venus' | 'Earth' | 'Moon' | 'Mars' | 'Jupiter' | 'Saturn' | 'Uranus' | 'Neptune' | 'Custom'
По умолчанию: 'Earth'

Планетарный экваториальный радиус, заданный как скаляр, в единицах измерения длины, которые задает параметр Units.

Зависимости

Чтобы включить этот параметр, установите Planet model равным Custom.

Программное использование

Параметры блоков: R
Тип: Вектор символов
Значения: скаляр
По умолчанию: '6378136.3'

Планетарный гравитационный параметр, заданный как скаляр, в единицах длины, кубированных в секунду за секунду, которые задает параметр Units.

Зависимости

Чтобы включить этот параметр, установите Planet model равным Custom.

Программное использование

Параметры блоков: GM
Тип: Вектор символов
Значения: скаляр
По умолчанию: '398600441500000'

Зональный гармонический коэффициент, заданный как массив с 3 элементами.

Зависимости

Чтобы включить этот параметр, установите Planet model равным Custom.

Программное использование

Параметры блоков: jvalue
Тип: Вектор символов
Значения: скаляр
По умолчанию: '[1.0826269e-03 -2.5323000e-06 -1.6204000e-06]'

Алгоритмы

Этот блок реализован с использованием следующих значений планетарных параметров для каждой планеты:

ПланетаЭкваториальный радиус (Re) в метрах Гравитационный параметр (GM) в м 3 / с2 Зональные гармонические коэффициенты
(Значения J)
Земля6378.1363e33.986004415e14[ 0.0010826269 -0.0000025323 -0.0000016204 ]
Юпитер71492e31.268e17[0.01475 0 -0.00058]
Марс3397.2e34.305e13 [ 0.001964 0.000036 ]
Меркурий2439.0e3 2.2032e130.00006
Луна1738.0e3 4902.799e90.0002027
Нептун24764e3 6.809e150.004
Сатурн60268e3 3.794e16 [0.01645 0 -0.001]
Уран25559e35.794e15 0.012
Венера6052.0e3 3.257e140.000027

Ссылки

[1] Валладо, Дэвид, Основы астродинамики и применения. Нью-Йорк: McGraw-Hill, 1997.

[2] Fortescue, P., J. Stark, G. Swinerd, eds.. Проектирование космических аппаратов, 3d ed. West Sussex: Wiley & Sons, 2003.

[3] Tewari, A. Boston: Моделирование и симуляция динамики атмосферного и космического рейса с MATLAB и Simulink. Бостон: Биркхойзер, 2007.

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

.

См. также

|

Введенный в R2009b

Документация Aerospace Blockset

Поддержка