Взаимное Соединение

Взаимная связь - это электромагнитное взаимодействие между антенными элементами в массиве. Ток, развиваемый в каждом антенном элементе массива, зависит от их собственного возбуждения, а также от вклада соседних антенных элементов. Взаимная связь обратно пропорциональна интервалу между различными антенными элементами в массиве. Взаимное связывание в массиве вызывает:

Изменения в диаграмме направленности излучения массива
Изменения импеданса входа отдельных антенных элементов в массиве

Чтобы охарактеризовать взаимное связывание, можно использовать взаимное сопротивление, S-параметры, матрицу связи или шаблон встроенного элемента.

Активный или сканирующий импеданс

Активное импеданс, или скан импеданс, является вход импедансом каждого антенного элемента в массив, когда все элементы возбуждены.

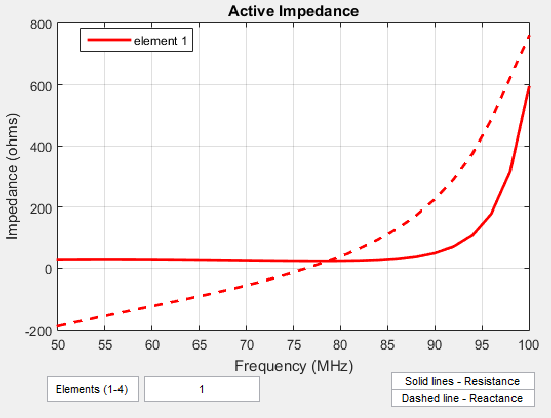
Активное импеданс массива зависит от:

Строение массива
Интервал между элементами
Сдвиг фазы, примененный к каждому элементу

Взаимное Сопротивление

Эффект взаимной связи наблюдается или моделируется путем изменения пространства между антенными элементами в массиве. Любое изменение межэлементных интервалов изменяет взаимное импеданс между антенными элементами. Для примера график показывает взаимное сопротивление двухэлементного дипольного массива как функцию межэлемента интервала.

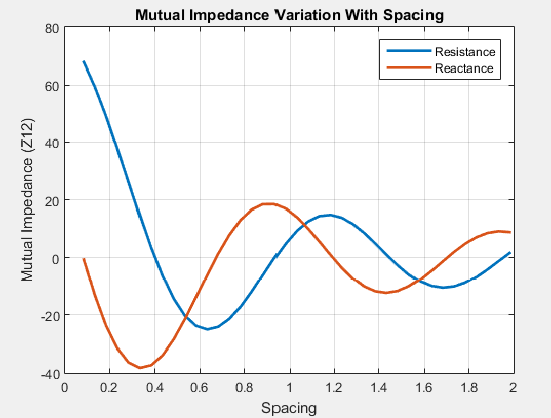
График показывает, что когда интервал между элементами увеличивается, взаимное сопротивление, и, следовательно, взаимное соединение уменьшается.

Матрица муфт

Матрица связи используется, чтобы охарактеризовать взаимную связь между антенными элементами на уровне порта. Эта матрица вычисляется с использованием S-параметров или Z-параметров и используется для развязки массива.

Матрица S-параметров

Чтобы вычислить связующую матрицу, можно использовать матрицу S-параметра. Вы вычисляете каждый столбец матрицы S-параметров путем подачи антенны в этом столбце по 1V. Рассмотрим массив элемента, расположенный в сетке 2x2. Визуализируйте сетку и номера элементов с помощью layout.

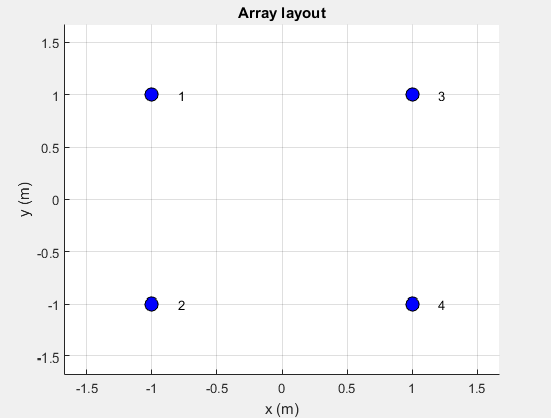
В этом массиве четыре порта. Соответствующая матрица S-параметров будет размером 4 x 4:

$S = (\begin{matrix} s_{11} & s_{12} & s_{13} & s_{14} \\ s_{21} & s_{22} & s_{23} & s_{24} \\ s_{31} & s_{32} & s_{33} & s_{34} \\ s_{41} & s_{42} & s_{43} & s_{44} \end{matrix})$

Во время этого измерения завершите работу остальных антенных элементов, используя эталонное сопротивление 50 Ом. Сопротивление отключения внутренне устанавливается на значение по умолчанию 50 Ом и может быть опущено во время вычисления. Если разрыв отличается, задайте значение сопротивления при использовании этой функции. Диагональные условия в показанной матрице представляют собой само-взаимодействие, которое также обычно упоминается как коэффициент отражения. Не-диагональные условия захватывают взаимную связь между портами антенны.

Использовать sparameters вычислить матрицу связи S-параметра массива в Antenna Toolbox™.

Умножение коэффициента и шаблона массива

Базис теории массивов является теоремой умножения шаблона. Эта теорема утверждает, что комбинированный шаблон N одинаковых элементов массива выражается как шаблон элемента, умножающий коэффициент массива.

Коэффициент массива вычисляется по формуле:

$A F = \sum_{i = 0}^{N} V (i) \cdot e^{j (k \sin θ \cos φ \cdot x (i) + k \sin θ \sin φ \cdot y (i) + k \cos θ \cdot z (i))}$

где:

N - количество элементов в массиве.
V - приложенное напряжение (амплитуда и фаза) для каждого элемента массива.
k - число волн.
theta и phi являются углами повышения и азимута.
x, y и z являются Декартовыми координатами мест подачи для каждого антенного элемента массива.

Если коэффициент массива вычисляется с помощью вышеописанного уравнения, можно вычислить диаграмму направленности массива как продукт коэффициента массива и диаграммы направленности отдельных антенных элементов массива.

Массив = AF * отдельный шаблон антенного элемента

Анализ принимает, что элементы массива отцеплены. Это означает, что ток в одном элементе не возбуждает токи в других элементах или нет взаимной связи между различными элементами массива. Это является самым серьезным ограничением теоремы о умножении шаблона, ограничивая его использование массивами с большим интервалом элементов.

Для примера:

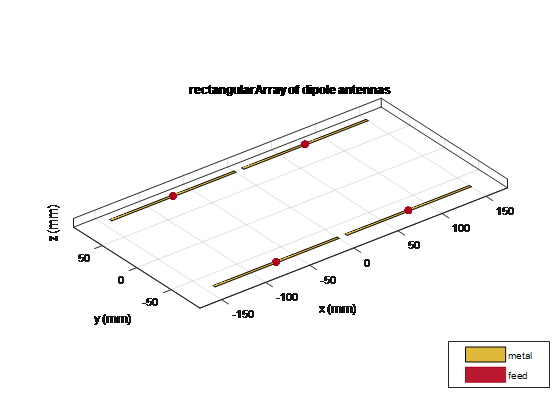
Вычислите шаблон прямоугольного массива диполей в плоскости x-y с интервалом в половину лямбды

fc = 1e9;
lambda = physconst('lightspeed')/fc;
az = -180:0.1:180;
el = -90:0.1:90;

%% Element
d = design(dipole,1e9);
d.Tilt = 90;
d.TiltAxis = [0 1 0];
 
%% Array
r = rectangularArray;
r.Element       = d;
r.RowSpacing    = lambda/2;
r.ColumnSpacing = lambda/2;
figure; show(r) ;
figure; patternMultiply(r, fc, az, el);

Увеличьте размер прямоугольного массива до 200 000 элементов. Ниже приведено время, необходимое для расчета и вычисленной направленности.

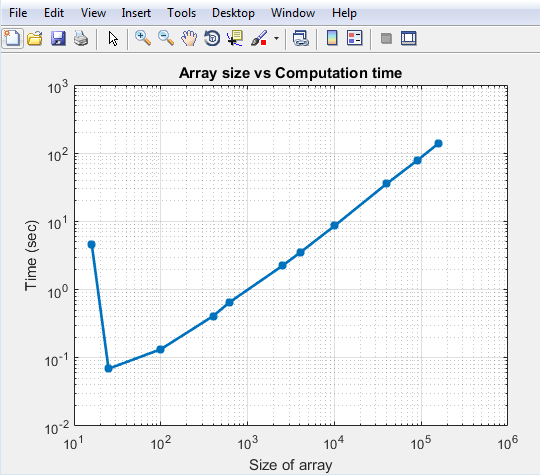
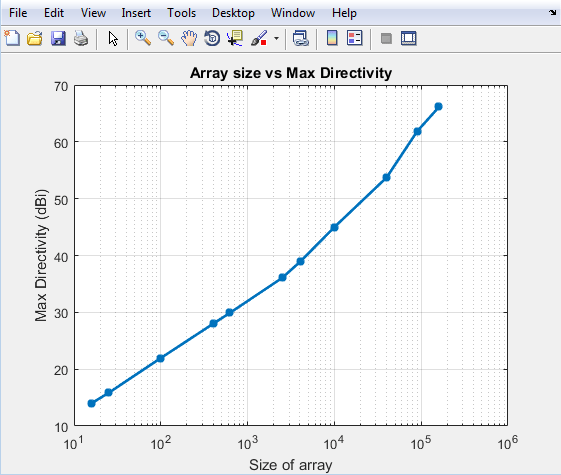
Вы видите, что время, необходимое для решения массива 100k, меньше 100 секунд. Начальное время выдавливания для малого массива связано с тем, что вы выполняете EM-анализ, чтобы вычислить шаблон отдельного дипольного элемента в массиве. После выполнения этого анализа результаты кэшируются, и последующие вызовы не выполняют никакого анализа EM. В результате увеличение времени довольно линейно. Это является самым большим преимуществом использования умножения шаблона. Он позволяет быстро решать большие массивы с ограниченными требованиями к памяти.

Шаблон изолированного элемента

Шаблоны отдельных элементов в небольших массивах значительно различаются. Поэтому вы не можете использовать умножение шаблона для полного шаблона массива, потому что изолированный шаблон элемента принимает, что все элементы имеют одинаковый шаблон.

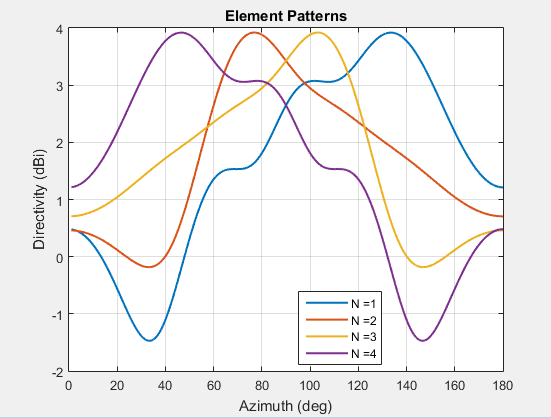
Можно вычислить полный шаблон массивов малых массивов, построив график шаблона всех элементов отдельно в небольшом массиве. Чтобы получить этот шаблон, каждый элемент возбуждается индивидуально, а остальные элементы массива заканчиваются с помощью опорного импеданса. Этот график показывает диаграмму направленности излучения отдельных элементов массива 4-- element.

Шаблон встраиваемого элемента

Шаблон встроенного элемента является шаблоном одного элемента, встроенного в конечный массив, рассчитанным путем приведения в действие определенного (обычно центрального) элемента в массиве. Остальные элементы массива прекращаются с помощью опорного импеданса. Этот метод полезен для большого массива, потому что захватывается эффект взаимной связи на отдельный элемент. Важно отметить, что эффекты ребра могут быть проигнорированы, поскольку размер массива принимается очень большим. Обычно для этого вычисления используется центральный антенный элемент. Из-за размера массива диаграмм направленности излучения элементов в массив могут быть аппроксимированы шаблоном встроенного элемента вместо шаблона изолированного элемента. Наконец, умножение шаблона используется, чтобы вычислить полный шаблон массива.

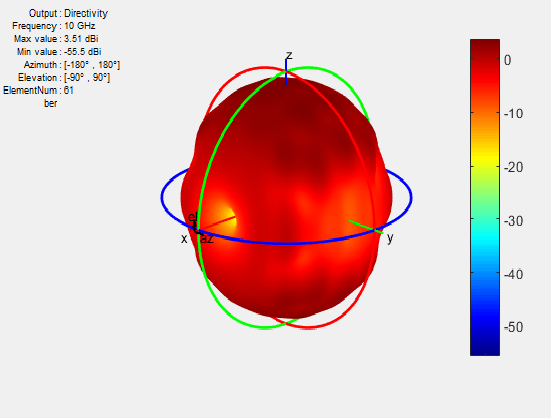
Рисунок показывает шаблон встроенного элемента центрального элемента в 11x11 массив. Можно также вычислить шаблон встроенного элемента как величину электрического поля.

Изолированный шаблон элемента не рекомендуется для больших массивов, так как этот метод не учитывает эффекты связи элементов вокруг него.

Скан слепоты

В больших массивах возможно, что направленность массива резко уменьшается при определенных углах скана. При этих сканах углах, называемых глухими углами, массив не излучает степень, подаваемый на своих входах выводах [3]. При использовании этих общих механизмов может возникнуть скан слепота:

Возбуждение поверхностных волн
Возбуждение лепестка решетки

Чтобы обнаружить слепоту скана в больших конечных массивах, исследуйте шаблон встроенного элемента. В бесконечном анализе массивов этот шаблон известен как шаблон элемента массива.

Ссылки

[1] Штуцман, У. Л. Тиле, G.A. Antenna Theory and Design, 3-е издание. Нью-Йорк: Уайли, 2013, с. 307.

Документация