Адаптивно настройте коэффициент усиления для выхода уровня постоянного сигнала
The comm.AGC Система object™ создает автоматический контроллер усиления (AGC), который адаптивно настраивает свой коэффициент усиления, чтобы достичь постоянного уровня сигнала на выходе. Для получения дополнительной информации см. Logarithmic-Loop AGC. Этот объект предназначен для потоковых приложений. Для получения дополнительной информации см. советы».
Чтобы адаптивно настроить коэффициент усиления для постоянного уровня сигнала на выходе:
Создайте comm.AGC Объекту и установите его свойства.
Вызывайте объект с аргументами, как будто это функция.
Дополнительные сведения о работе системных объектов см. в разделе «Что такое системные объекты?».
agc = comm.AGC
agc = comm.AGC(Name,Value)AdaptationStepSize', 0.05 устанавливает размер шага для обновлений усиления равным 0.05.
Если не указано иное, свойства являются нетронутыми, что означает, что вы не можете изменить их значения после вызова объекта. Объекты блокируются, когда вы вызываете их, и release функция разблокирует их.
Если свойство настраивается, можно изменить его значение в любой момент.
Для получения дополнительной информации об изменении значений свойств смотрите Разработку системы в MATLAB Использование Системных объектов.
AdaptationStepSize - Размер шага для обновлений усиления0.01 (по умолчанию) | положительная скалярная величинаРазмер шага для обновлений усиления, заданный как положительная скалярная величина. Увеличение размера шага позволяет AGC быстрее реагировать на изменения уровня входного сигнала, но увеличений изменение уровня выхода сигнала после достижения установившейся операции. Для получения дополнительной информации смотрите Критерии эффективности AGC, и Vary AGC Step Size, и Plot Effect of Step Size на примерах эффективности AGC.
Настраиваемый: Да
Типы данных: double
DesiredOutputPower - Целевой выход степени1 W (по умолчанию) | положительная скалярная величинаЦелевой выход степени уровень, заданный как положительная скалярная величина. Степень измеряется в Ваттах, относящихся к 1 ому. Для получения дополнительной информации смотрите Адаптивно Настроить Амплитуду Принимаемого Сигнала Используя пример AGC.
Типы данных: double
AveragingLength - Длина окна усреднения100 выборки (по умолчанию) | положительным целым числомДлина окна усреднения в выборках, заданная как положительное целое число. Для получения дополнительной информации о том, как средняя длина влияет на отклонение выходного сигнала AGC в установленной операции и скорость выполнения, см. Советы и пример переменной средней длины AGC.
Типы данных: double
MaxPowerGain - Максимальный коэффициент усиления степени60 дБ (по умолчанию) | положительная скалярная величинаМаксимальный коэффициент усиления степени в децибелах, заданный как положительная скалярная величина. Большие регулировки усиления могут вызвать усечение, когда небольшой входной сигнал степени внезапно увеличиться. Используйте это свойство, чтобы избежать больших регулировок усиления путем ограничения усиления, которое AGC применяет к входному сигналу. Для получения дополнительной информации смотрите примеры максимального усиления Vary AGC и демонстрации эффекта максимального усиления AGC на пакетных данных.
Типы данных: double
y = agc(x)
[ возвращает y,powerlevel] = agc(x)powerlevel, оценка уровня степени входного сигнала. Можно использовать powerlevel в качестве выходного сигнала детектора энергии.
x - Входной сигналВходной сигнал, заданный как вектор-столбец.
Типы данных: single | double
Поддержка комплексного числа: Да
y - Выходной сигналВыход сигнал, возвращенный как вектор-столбец. Выходной сигнал является совпадающим типом данных, что и входной сигнал, x.
powerlevel - Оценка уровня степениОценка уровня мощности, возвращенная как N вектор-столбец S-элемента. N S - длина входного сигнала, x. Можно использовать powerlevel в качестве выходного сигнала детектора энергии.
Чтобы использовать функцию объекта, задайте системный объект в качестве первого входного параметра. Например, чтобы освободить системные ресурсы системного объекта с именем obj, используйте следующий синтаксис:
release(obj)
Примените различные длины среднего AGC к сигналам, модулированным QAM. Сравните отклонение и график сигналов после применения AGC.
Создайте три объекта системы AGC со средними длинами окон, установленными на 10, 100 и 1000 выборки, соответственно.
agc1 = comm.AGC('AveragingLength',10); agc2 = comm.AGC('AveragingLength',100); agc3 = comm.AGC('AveragingLength',1000);
Сгенерируйте 16-QAM модулированные и повышенные пакетированные данные в форме косинусоидного импульса.
M = 16; d = randi([0 M-1],1000,1); s = qammod(d,M); x = 0.1*s; pulseShaper = comm.RaisedCosineTransmitFilter; y = awgn(pulseShaper(x),inf);
Применить AGC к данным, собирающим отдельные выходы для каждого объекта AGC.
r1 = agc1(y); r2 = agc2(y); r3 = agc3(y);
Постройте и сравните сигналы. Когда средняя длина увеличивается, отклонение на выходе AGC уменьшается.
figure(1) subplot(4,1,1) plot(abs(y)) title('AGC Input') subplot(4,1,2) plot(abs(r1)) axis([0 8000 0 10]) title('AGC Output (Averaging Length is 10 Samples)') text(4000,5,sprintf('Variance is %f',var(r1(3000:end)))) subplot(4,1,3) plot(abs(r2)) axis([0 8000 0 10]) title('AGC Output (Averaging Length is 100 Samples)') text(4000,5,sprintf('Variance is %f',var(r2(3000:end)))) subplot(4,1,4) plot(abs(r3)) axis([0 8000 0 10]) title('AGC Output (Averaging Length is 1000 Samples)') text(4000,5,sprintf('Variance is %f',var(r3(3000:end))))

Примените различные максимальные уровни усиления AGC к сигналам, модулированным QPSK. Сравните график сигналов после применения AGC.
Создайте три объекта системы AGC с их максимальными значениями усиления, установленными на 10, 20 и 30 дБ соответственно.
agc1 = comm.AGC('MaxPowerGain',10); agc2 = comm.AGC('MaxPowerGain',20); agc3 = comm.AGC('MaxPowerGain',30);
Сгенерируйте модулированные QPSK данные. Передайте данные через повышенную импульсную фильтрацию косинуса и канал AWGN.
M = 4; pktLen = 10000; d = randi([0 M-1],pktLen,1); s = pskmod(d,M,pi/4); x = repmat([zeros(pktLen,1); 0.3*s],3,1); pulseShaper = comm.RaisedCosineTransmitFilter; y = awgn(pulseShaper(x),50);
Применить AGC к данным, собирающим отдельные выходы для каждого объекта AGC.
r1 = agc1(y); r2 = agc2(y); r3 = agc3(y);
Постройте график входного сигнала и регулируемого AGC сигнала с различными максимальными уровнями усиления. Сравните результаты для условий в этом примере.
Настройка максимального усиления 10 дБ слишком мала, и выход AGC не достигает желаемого уровня выходного сигнала, рискуя потерей данных из-за уменьшения динамической области значений сигналов.
Максимальная настройка усиления 20 дБ оптимальна, и выход AGC достигает желаемого уровня без потерь сигнала из-за насыщения.
Настройка максимального усиления 30 дБ слишком велика, и выход AGC перерегулирует требуемый уровень сигнала, рискуя насыщением сигнала и потерей данных в начале принятых пакетов.
Между пакетами входной сигнал содержит только шум.
Как показано на графиках, пакетные передачи имеют длительные периоды, когда данные не получены. Длительные периоды без полученных данных приводят к увеличению AGC до максимального значения усиления. Если пакет приходит, когда коэффициент усиления АРУ слишком высок, выход степени перерегулирует требуемый уровень сигнала, пока АРУ не сможет ответить на изменение уровня входа степени и уменьшить его коэффициент усиления.
limits = [0 3]; figure(1) subplot(4,1,1) plot(abs(y)) ylim(limits) title('AGC Input') subplot(4,1,2) plot(abs(r1)) ylim(limits) title('AGC Output (Maximum Power Gain is 10 dB)') subplot(4,1,3) plot(abs(r2)) ylim(limits) title('AGC Output (Maximum Power Gain is 20 dB)') subplot(4,1,4) plot(abs(r3)) ylim(limits) title('AGC Output (Maximum Power Gain is 30 dB)')

Постройте график сигнала и оценки уровня степени. Сравните результаты. Оценка уровня степени может служить детектором степени, указывающим точно, когда полученный пакет пришел.
Создайте объект AGC System с его максимальным значением усиления, установленным на 20 дБ.
agc20 = comm.AGC('MaxPowerGain',20);Сгенерируйте модулированные QPSK данные. Передайте данные через повышенную импульсную фильтрацию косинуса и канал AWGN.
modOrd = 4; % Modulation order pktLen = 10000; % Packet length d = randi([0 modOrd-1],pktLen,1); s = pskmod(d,modOrd,pi/4); x = repmat([zeros(pktLen,1); 0.3*s],3,1); pulseShaper = comm.RaisedCosineTransmitFilter; y = awgn(pulseShaper(x),50);
Применить AGC к данным, собирающим отдельные выходы для каждого объекта AGC.
[r2,p2] = agc20(y);
Постройте график входного сигнала и оценки уровня степени принимаемого сигнала. Сравните результаты. Прием пакетированных данных с длительными периодами, когда данные не получены, приводит к снижению обнаруженной оценки уровня степени почти до нуля. В то время как входной сигнал обнаруживается, выход степени оценивается, p2, служит детектором степени, указывающим точно, когда полученный пакет пришел.
limits = [0 3]; figure(1) subplot(4,1,1) plot(abs(y)) ylim(limits) title('AGC Input') subplot(4,1,2) plot(abs(p2)) title('Power Level')

Примените различные размеры шагов AGC к сигналам, модулированным QPSK. Сравните сигналы после применения AGC.
Создайте три объекта системы AGC с установленными размерами шагов 1e-1, 1e-3 и 1e-4 соответственно.
agc1 = comm.AGC('AdaptationStepSize',1e-1); agc2 = comm.AGC('AdaptationStepSize',1e-3); agc3 = comm.AGC('AdaptationStepSize',1e-4);
Сгенерируйте модулированные QPSK данные с повышенным формированием косинусоидного импульса.
d = randi([0 3],500,1); s = pskmod(d,4,pi/4); x = 0.1*s; pulseShaper = comm.RaisedCosineTransmitFilter; y = pulseShaper(x);
Применить AGC к данным, собирающим отдельные выходы для каждого объекта AGC.
r1 = agc1(y); r2 = agc2(y); r3 = agc3(y);
Постройте график входа и выходного сигнала после различных размеров шага AGC.
С размером шага, установленным на 1e-1, перерегулирование выходного сигнала AGC становится заметным. Сигнал выхода сходится очень быстро.
С размером шага, установленным на 1e-3, выход сигнала AGC исчезает. Выходной сигнал постепенно сходится.
С размером шага, установленным на 1e-4, выходной сигнал AGC занимает от 2 до 3 раз больше, чем размер шага 1e-3.
figure subplot(4,1,1) plot(abs(y)) title('AGC Input') subplot(4,1,2) plot(abs(r1)) title('AGC Output (Adaption Step Size is 1e-1)') subplot(4,1,3) plot(abs(r2)) title('AGC Output (Adaption Step Size is 1e-3)') subplot(4,1,4) plot(abs(r3)) title('AGC Output (Adaption Step Size is 1e-4)')

Модулируйте и усильте сигнал QPSK. Установите амплитуду принимаемого сигнала приблизительно 1 В при помощи AGC. Постройте график выхода.
Создайте сигнал с модуляцией QPSK при помощи объекта QPSK System.
data = randi([0 3],1000,1); qpsk = comm.QPSKModulator; modData = qpsk(data);
Ослабьте модулированный сигнал.
txSig = 0.1*modData;
Создайте объект AGC System и передайте через него переданный сигнал. АРУ регулирует степень принимаемого сигнала приблизительно на 1 Вт.
agc = comm.AGC; rxSig = agc(txSig);
Постройте график сигнальных созвездий передающего и принятого сигналов после того, как AGC достигнет установившегося состояния.
h = scatterplot(txSig(200:end),1,0,'*'); hold on scatterplot(rxSig(200:end),1,0,'or',h); legend('Input of AGC','Output of AGC')

Измерьте и сравните степень переданных и принятых сигналов после того, как AGC достигнет устойчивого состояния. Степень переданного сигнала в 100 раз меньше, чем степень принимаемого сигнала.
txPower = var(txSig(200:end)); rxPower = var(rxSig(200:end)); [txPower rxPower]
ans = 1×2
0.0100 0.9970
Создайте два objects™ системы AGC, чтобы настроить уровень принимаемого сигнала с помощью двух различных размеров шага с одинаковыми периодами обновления.
Сгенерируйте сигнал 8-PSK таким образом, чтобы его степень составляла 10 Вт.
data = randi([0 7],200,1);
modData = sqrt(10)*pskmod(data,8,pi/8,'gray');Создайте пару приподнятых косинусоидных согласованных фильтров с их Gain набор свойств так, чтобы они имели единую выходную степень.
txfilter = comm.RaisedCosineTransmitFilter('Gain',sqrt(8)); rxfilter = comm.RaisedCosineReceiveFilter('Gain',sqrt(1/8));
Пропустите модулированный сигнал через фильтр передачи приподнятого косинуса.
txSig = txfilter(modData);
Создайте два объекта системы AGC, чтобы настроить уровень принимаемого сигнала. Установите размер шага 0,01 и 0,1, соответственно.
agc1 = comm.AGC('AdaptationStepSize',0.01); agc2 = comm.AGC('AdaptationStepSize',0.1);
Примените AGC к модулированному сигналу, захватывающему отдельные выходы для каждого объекта AGC.
agcOut1 = agc1(txSig); agcOut2 = agc2(txSig);
Фильтрация выходных сигналов AGC при помощи приподнятого приёмного фильтра косинуса.
rxSig1 = rxfilter(agcOut1); rxSig2 = rxfilter(agcOut2);
Постройте график степени фильтрованных реакций AGC с учетом задержки 10 символов через пару фильтра приема и передачи.
plot([abs(rxSig1(11:110)).^2 abs(rxSig2(11:110)).^2]) grid on xlabel('Symbols') ylabel('Power (W)') legend('Step size 0.01','Step size 0.1')

Сигнал с большим размером шага быстрее сходится к целевому уровню степени AGC 1 Вт.
Постройте график степени статических фильтрованных сигналов AGC путем включения только последних 100 символов. Больший размер шага AGC приводит к менее точной коррекции усиления. Большие значения размера шага AGC приводят к более быстрому сходимости за счет менее точного управления усилением.
plot((101:200),[abs(rxSig1(101:200)).^2 abs(rxSig2(101:200)).^2]) grid on xlabel('Symbols') ylabel('Power (W)') legend('Step size 0.01','Step size 0.1')

Передайте ослабленные пакетные данные QPSK в два AGC с различными максимальными усилениями. Постройте график результатов.
Создайте два пакета данных QSPK с 200 символами. Передайте пакеты через 1200-символьную систему координат.
modData1 = pskmod(randi([0 3],200,1),4,pi/4); modData2 = pskmod(randi([0 3],200,1),4,pi/4); txSig = [modData1; zeros(400,1); modData2; zeros(400,1)];
Ослабьте переданный сигнал пакетной передачи на 20 дБ и постройте график его степени.
rxSig = 0.1*txSig; rxSigPwr = abs(rxSig).^2; plot(rxSigPwr) grid xlabel('Symbols') ylabel('Power (W)') title('Signal Power Before Applying AGC')

Создайте два AGC с максимальным коэффициентом усиления степени 30 дБ и 24 дБ соответственно.
agc1 = comm.AGC('MaxPowerGain',30,'AdaptationStepSize',0.02); agc2 = comm.AGC('MaxPowerGain',24,'AdaptationStepSize',0.02);
Применить AGC к ослабленному сигналу, захватывающему отдельные выходы для каждого объекта AGC. Вычислим выход степени для каждого случая.
rxAGC1 = agc1(rxSig); rxAGC2 = agc2(rxSig); pwrAGC1 = abs(rxAGC1).^2; pwrAGC2 = abs(rxAGC2).^2;
Постройте график выходных степеней. Первоначально для второго пакета agc1 выходная степень сигнала слишком высока, потому что AGC приложил свой максимальный коэффициент усиления в течение периода, когда данные не были переданы. Соответствующий agc2 выходная степень (2,5 Вт) перерегулирует целевой уровень степени 1 Вт на значительно меньше, чем agc1 Выход степени сигнала (10 Вт). Время сходимости для agc2 короче, чем время сходимости для agc1, потому что входной вход agc2 применяет меньший максимальный коэффициент усиления, чем agc1.
plot([pwrAGC1 pwrAGC2]) legend('AGC1','AGC2') grid xlabel('Symbols') ylabel('Power (W)') title('Signal Power After Applying AGC')

Реализация AGC использует логарифмический цикл обратной связи. Как показывает этот рисунок алгоритма AGC с логарифмическим циклом, выходной сигнал является продуктом входного сигнала и экспоненциала усиления цикла. Сигнал ошибки является различием между уровнем ссылки и продукта логарифма детектора выхода и экспоненциала усиления цикла. После умножения на размер шага AGC передает сигнал ошибки интегратору.
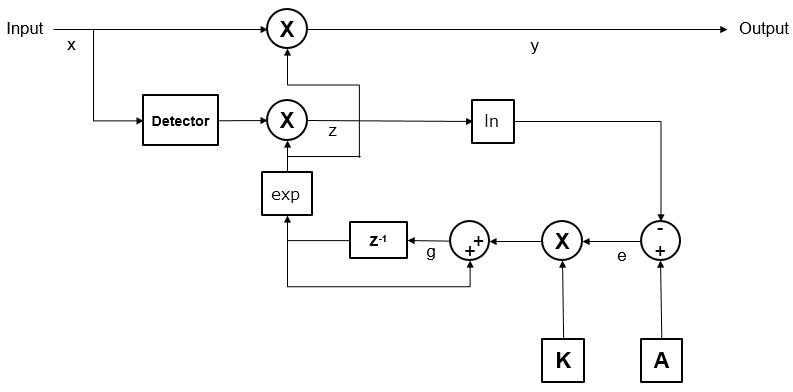
AGC с логарифмическим циклом хорошо работает для различных типов сигналов, включая амплитудную модуляцию. Детектор AGC применяется к входному сигналу, который улучшает время сходимости, но увеличивает изменение степени сигнала на входе детектора. Большие изменения сигнала на входе детектора приемлемы для систем с плавающей точкой.
Математически алгоритм суммируется как
где:
x - входной сигнал.
y - сигнал выхода.
g - коэффициент усиления цикла.
D(•) является функцией детектора.
z - выход детектора.
A - ссылочное значение.
e - сигнал ошибки.
K - размер шага.
Выход детектора AGC, z, вычисляет детектор квадратного закона, заданный как
где N - период обновления. Детектор квадратного закона формирует выход, пропорциональный квадрату входного сигнала y.
Увеличение размера шага уменьшает время атаки и время затухания, но также увеличивает накачку усиления.
Время атаки - длительность, требуемая для ответа AGC на увеличение амплитуды входа
Время затухания - длительность, принятая для AGC, чтобы ответить на уменьшение амплитуды входа
Накачка усиления - изменение значения усиления во время установившейся операции
Этот Системный объект предназначен для потоковых приложений.
Если амплитуда сигнала не меняется в системе координат, можно симулировать идеальный AGC, вычислив средний коэффициент усиления, требуемый для системы координат выборок. Затем примените коэффициент усиления к каждой выборке в системе координат.
Если вы используете AGC с сигналами QAM более высокого порядка, вам может потребоваться уменьшить изменение усиления во время статической операции. Осмотрите сигнальное созвездие на выходе АРУ при установленной операции. Можно увеличить среднюю длину, чтобы избежать частых регулировок усиления. Увеличение средней длины уменьшает скорость выполнения.
Указания и ограничения по применению:
Смотрите Системные объекты в Генерации кода MATLAB (MATLAB Coder).
У вас есть измененная версия этого примера. Вы хотите открыть этот пример с вашими правками?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.