Спектр вычислений расстояния сверточного кода
spect = distspec(trellis,n)
spect = distspec(trellis)
spect = distspec(trellis,n) вычисляет свободное расстояние и первое n компоненты весового и дистанционного спектров линейного сверточного кода. Поскольку сверточные коды не имеют контуров блоков, спектр веса и спектр расстояния являются полунепрерывными и чаще всего аппроксимируются первыми несколькими компонентами. Область входа trellis является действительной структурой решетки MATLAB, как описано в Trellis Description of a Convolutional Code. Выход, spect, является структурой с этими полями:
| Область | Значение |
|---|---|
spect.dfree | Свободное расстояние кода. Это минимальное количество ошибок в закодированной последовательности, необходимых для создания события ошибки. |
spect.weight | A- n вектор, который приводит общее количество информационных битовых ошибок в событиях ошибки, перечисленных в spect.event. |
spect.event | A- n вектор, в котором указывается количество событий ошибок для каждого расстояния между spect.dfree и spect.dfree+n-1. Вектор представляет первую n компоненты спектра расстояний. |
spect = distspec(trellis) то же, что и spect = distspec(trellis,1).
Приведенный ниже пример выполняет следующие задачи:
Вычисляет спектр расстояния для сверточного кода скорости 2/3, который изображен на странице с описанием для poly2trellis функция
Использует выход distspec как вход в bercoding функция, чтобы найти теоретическую верхнюю границу по вероятности битовой ошибки для системы, которая использует этот код с когерентной модуляцией BPSK
Строит графики верхней границы с помощью berfit функция
trellis = poly2trellis([5 4],[23 35 0; 0 5 13]) spect = distspec(trellis,4) berub = bercoding(1:10,'conv','hard',2/3,spect); % BER bound berfit(1:10,berub); ylabel('Upper Bound on BER'); % Plot.
Выходы и график представлены ниже.
trellis =
numInputSymbols: 4
numOutputSymbols: 8
numStates: 128
nextStates: [128x4 double]
outputs: [128x4 double]
spect =
dfree: 5
weight: [1 6 28 142]
event: [1 2 8 25]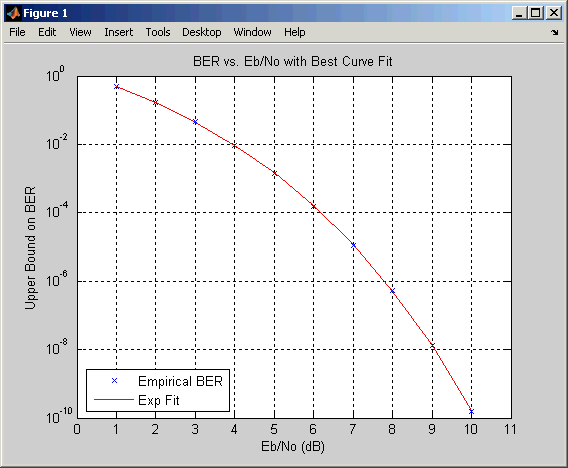
Функция использует алгоритм поиска дерева, реализованный со стеком, как описано в [2].
[1] Бочарова И. Е. и Б. Д. Кудряшов, «Рациональная ставка проколотых сверточных кодов для мягкого декодирования Viterbi», Транзакции IEEE по теории информации, том 43, № 4, июль 1997, стр. 1305-1313.
[2] Cedervall, M. and R. Johannesson, «A Fast Algorithm for Computing Distance Spectrum of Convolutional Codes», IEEE Transactions on Information Theory, Vol. 35, No6, Nov. 1989, pp. 1146-1159.
[3] Chang, J., D. Hwang, and M. Lin, «Some Extended Results on the Search for Good Convolutional Codes», IEEE Transactions on Information Theory, Vol. 43, No. 5, Sep. 1997, pp. 1682-1697.
[4] Frenger, P., P. Orten, and T. Ottosson, «Comments and Additions to Recent Papers on New Convolutional Codes», IEEE Transactions on Information Theory, Vol. 47, No. 3, March 2001, pp. 1199-1201.