Обнаружение ошибок в принятых системах координат кодового слова в соответствии с полиномом генератора
Communications Toolbox/Обнаружение и исправление ошибок/CRC
Блок General CRC Syndrome Detector вычисляет контрольные суммы циклической проверки избыточности (CRC) для принятых систем координат кодового слова. Для успешного обнаружения CRC в ссылке коммуникационной системы необходимо выровнять настройки параметра блока General CRC Syndrome Detector с парным блоком General CRC Generator.
Для получения дополнительной информации см. «Операция детектора синдрома CRC».
In - Получено кодовое словоПолучено кодовое слово, заданное как двоичный вектор-столбец.
Типы данных: double | Boolean
Out - Выходная система координатВыходная система координат, возвращенный как двоичный вектор-столбец, который наследует тип данных входного сигнала. Выходная система координат содержит полученное кодовое слово с удаленными контрольными суммами.
Длина выходной системы координат n - k * r битах, где n - размер полученного кодового слова, k - количество контрольных сумм на систему координат, а r - степень полинома генератора.
Err - Сигнал ошибки контрольной суммыСигнал ошибки контрольной суммы, возвращенный как двоичный вектор-столбец, который наследует тип данных входного сигнала. Длина Err равен значению Checksums per frame. Для каждого расчета контрольной суммы значение элемента 0 в Err указывает на отсутствие ошибки контрольной суммы и значение элемента 1 в Err указывает на ошибку контрольной суммы.
Generator polynomial - Полином генератора'z^16 + z^12 + z^5 + 1' (по умолчанию) | полиномиальный вектор символов | двоичный вектор-строка | целочисленный вектор-строкаПолином генератора для алгоритма CRC, заданный как один из следующих:
Полиномиальный вектор символов, такой как 'z^3 + z^2 + 1'.
Двоичный вектор-строка, который представляет коэффициенты полинома генератора в порядке убывания степени. Длина этого вектора (N + 1), где N - степень полинома генератора. Для примера, [1 1 0 1] представляет полином x3+ z2+ 1.
Целое число вектора-строки, содержащее степени z для ненулевых членов в полиноме в порядке убывания. Для примера, [3 2 0] представляет полином z3 + z2 + 1.
Для получения дополнительной информации смотрите Представление символов полиномов.
Некоторые обычно используемые полиномы генератора включают:
| Метод CRC | Полином генератора |
|---|---|
| CRC-32 | 'z^32 + z^26 + z^23 + z^22 + z^16 + z^12 + z^11 + z^10 + z^8 + z^7 + z^5 + z^4 + z^2 + z + 1' |
| CRC-24 | 'z^24 + z^23 + z^14 + z^12 + z^8 + 1' |
| CRC-16 | 'z^16 + z^15 + z^2 + 1' |
| Сторнированные CRC-16 | 'z^16 + z^14 + z + 1' |
| CRC-8 | 'z^8 + z^7 + z^6 + z^4 + z^2 + 1' |
| CRC-4 | 'z^4 + z^3 + z^2 + z + 1' |
Пример: 'z^7 + z^2 + 1', [1 0 0 0 0 1 0 1], и [7 2 0] представляют тот же полином, p (z) =
z7 + z
2 + 1.
Initial states - Начальные состояния регистра внутреннего сдвига0 (по умолчанию) | 1 | двоичные векторы-строкиНачальные состояния внутреннего регистра сдвига, заданные как двоичный скаляр или двоичный вектор-строка с длиной, равной степени полинома генератора. Скалярное значение расширяется до вектора-строки равной длины до степени полинома генератора.
Direct method - Используйте прямой алгоритм для вычисления контрольной суммы CRCoff (по умолчанию) | onВыберите, чтобы использовать прямой алгоритм для вычислений контрольной суммы CRC. При снятии блок использует непрямой алгоритм для вычислений контрольной суммы CRC.
Для получения дополнительной информации о прямых и непрямых алгоритмах см. Выявление ошибок и Коррекцию.
Reflect input bytes - Отражает входные байтыoff (по умолчанию) | onВыберите, чтобы развернуть полученное кодовое слово в байтовом базисе перед вводом данных в регистр сдвига. Когда Reflect input bytes выбран, полученная длина кодового слова, разделенная на значение параметра Checksums per frame, должна быть целым числом и кратной 8. Когда Reflect input bytes очищена, блок не поворачивает входные данные.
Reflect checksums before final XOR - Отражать контрольные суммы перед окончательным XORoff (по умолчанию) | onВыберите Reflect checksums before final XOR, чтобы развернуть контрольные суммы CRC вокруг их центров после того, как входные данные будут полностью пройдены через сдвиг регистр. Когда Reflect checksums before final XOR снят, блок не поворачивает контрольные суммы CRC.
Final XOR - Окончательный XOR0 (по умолчанию) | 1 | двоичные векторы-строкиКонечный XOR, заданный как двоичный скаляр или двоичный вектор-строка с длиной, равной степени полинома генератора. Операция XOR запусков с использованием значения параметра Final XOR и контрольной суммы CRC перед сравнением с контрольной суммой входа. Скалярное значение расширяется до вектора-строки равной длины до степени полинома генератора. Настройка 0 эквивалентно отсутствию операции XOR.
Checksums per frame - Количество контрольных сумм, рассчитанных для каждой системы координат1 (по умолчанию) | положительное целое числоКоличество контрольных сумм, вычисленных для каждой системы координат, заданное в виде положительного целого числа.
Типы данных |
|
Многомерные сигналы |
|
Сигналы переменного размера |
|
Циклическое кодирование с проверкой избыточности (CRC) является методом кодирования с управлением ошибками для обнаружения ошибок, которые возникают при передаче системы координат данных. В отличие от блочных или сверточных кодов, коды CRC не имеют встроенной возможности исправления ошибок. Вместо этого, когда коммуникационная система обнаруживает ошибку в принятом кодовом слове, приемник запрашивает отправителя повторно передать кодовое слово.
При кодировании CRC передатчик применяет правило к каждой системе координат данных, чтобы создать дополнительные биты CRC, называемые контрольной суммой или синдромом, и затем добавляет контрольную сумму к системе координат данных. После приема переданного кодового слова приемник применяет то же самое правило к принятому кодовому слову. Если полученная контрольная сумма ненулевая, произошла ошибка, и передатчик должен повторно отправить систему координат данных.
Когда количество контрольных сумм в систему координат больше 1, входные системы координат данных разделяются на подкадры, правило применяется к каждому подкадру данных, и отдельные контрольные суммы добавляются к каждому подкадру. Кодовые слова подкадров объединены для вывода одной системы координат.
Для обсуждения поддерживаемых алгоритмов CRC смотрите Циклические проверки кода избыточности.
Детектор синдрома CRC выводит принятую систему координат сообщения и вектор ошибки контрольной суммы в соответствии с заданным полиномом генератора и количеством контрольных сумм на систему координат.
Биты контрольной суммы удалены из каждой нижней рамы, так, чтобы получающимся, которое длина системы координат выхода n - <reservedrangesplaceholder5> × <reservedrangesplaceholder4>, где n размер полученного ключевого слова, k, было количество контрольных сумм за систему координат, и r степень полинома генератора. Входной кадр должен быть равномерно разделен на k.
Для определенного начального состояния внутреннего сдвига регистра:
Принятое кодовое слово разделено на k подкадра равного размера.
CRC удаляется из каждого из k подкадров и сравнивается с контрольной суммой, вычисленной на принятых подкадрах кодового слова.
Выход системы координат собирается путем конкатенации бит субкадров k и затем выводится как вектор-столбец.
Ошибка контрольной суммы выводится как двоичный вектор-столбец k длины. Значение элемента 0 указывает на свободный от ошибок принятый подкадр, а значение элемента 1 указывает на ошибку, возникшую в принятом подкадре.
Для сценария, показанного здесь, принимается 16-битовое кодовое слово, полином генератора третьей степени вычисляет контрольную сумму CRC, начальное состояние составляет 0, и количество контрольных сумм на систему координат составляет 2.
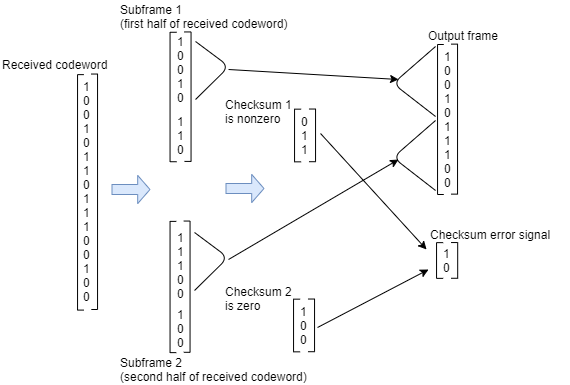
Поскольку количество контрольных сумм в систему координат составляет 2, а полином генератора степени равен 3, принятое кодовое слово разделяется пополам, и вычисляются две контрольные суммы размера 3, по одной для каждой половины принятого кодового слова. Начальные состояния не показаны, потому что начальное состояние [0] не влияет на выход алгоритма CRC. Выходная система координат содержит конкатенацию двух половин принятого кодового слова в качестве единственного вектора размера 10. Выход ошибки контрольной суммы содержит двухкомпонентный вектор системы координат 2 на 1, значения которого зависят от того, равны ли вычисленные контрольные суммы нулю. Как показано на рисунке, первая контрольная сумма ненулевая, а вторая контрольная сумма равна нулю, что указывает на ошибку при приеме первой половины кодового слова.
[1] Склар, Бернард. Цифровые коммуникации: основы и приложения. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1988.
[2] Wicker, Stephen B. Системы управления ошибками для цифровой связи и хранения данных. Верхняя Седловая река, Нью-Джерси: Prentice Hall, 1995.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.
