Этот пример подходит для двух плохо разрешенных Гауссовых peaks на распадающемся экспоненциальном фоне с помощью общей (нелинейной) пользовательской модели.
Подгонка данных с помощью этого уравнения
где ai пиковые амплитуды, bi являются пиковыми центроидами, и ci связаны с пиковыми ширинами. Поскольку неизвестные коэффициенты являются частью экспоненциальных аргументов функции, уравнение нелинейно.
Загрузите данные и откройте приложение Аппроксимирование Кривыми:
load gauss3 cftool
Рабочая область содержит две новые переменные:
xpeak является вектором значений предиктора.
ypeak является вектором значений отклика.
В приложении Аппроксимирование Кривыми выберите xpeak для X data и ypeak для Y data.
Введите Gauss2exp1 для Fit name.
Выберите Custom Equation для типа модели.
Замените текст примера в поле редактирования уравнения следующими терминами:
a*exp(-b*x)+a1*exp(-((x-b1)/c1)^2)+a2*exp(-((x-b2)/c2)^2)
Подгонка плоха (или неполна) в этой точке, потому что начальные точки выбраны случайным образом, и никакие коэффициенты не имеют границ.
Задайте разумные начальные точки коэффициентов и ограничения. Вывод начальных точек особенно прост для текущей модели, потому что Гауссовы коэффициенты имеют простую интерпретацию, и экспоненциальный фон четко задан. Кроме того, поскольку пиковые амплитуды и ширины не могут быть отрицательными, ограничивайте a 1, a 2, c 1 и c 2, чтобы они были больше 0.
Нажмите Fit Options.
Измените Lower границу для a 1, a 2, c 1 и c 2 на 0, так как пиковые амплитуды и ширины не могут быть отрицательными.
Введите начальные точки, как показано для неизвестных коэффициентов.
| Неизвестные | Начальная точка |
|---|---|
a | 100 |
a1 | 100 |
a2 | 80 |
b | 0.1 |
b1 | 110 |
b2 | 140 |
c1 | 20 |
c2 | 20 |

Когда вы изменяете опции подгонки, приложение Аппроксимирование Кривыми обновляется. Нажмите Enter или закройте диалоговое окно «Опции подгонки», чтобы убедиться, что последнее изменение применено к подгонке.
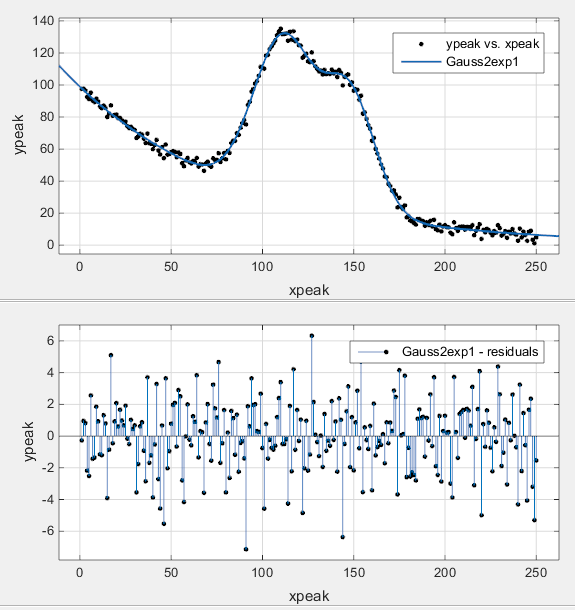
Ниже приведены подгонка и невязки.