Динамические сети можно разделить на две категории: те, которые имеют только обратные соединения, и те, которые имеют обратную связь, или регулярные соединения. Чтобы понять различия между статическими, динамическими и рекуррентно-динамическими сетями, создайте некоторые сети и посмотрите, как они реагируют на вход последовательность. (Во-первых, можно хотеть просмотреть Simulation with Sequential Inputs in a Dynamic Network.)
Следующие команды создают импульсную входную последовательность и строят график:
p = {0 0 1 1 1 1 0 0 0 0 0 0};
stem(cell2mat(p))

Теперь создайте статическую сеть и найдите сетевую реакцию на импульсную последовательность. Следующие команды создают простую линейную сеть с одним слоем, одним нейроном, без смещения и весом 2:
net = linearlayer;
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.IW{1,1} = 2;
view(net)

Теперь можно симулировать сетевой ответ на импульсный вход и построить его:
a = net(p); stem(cell2mat(a))

Обратите внимание, что реакция статической сети длится так же долго, как и вход импульс. Реакция статической сети в любой момент точки зависит только от значения последовательности входа в то же время точки.
Теперь создайте динамическую сеть, но такую, которая не имеет никаких обратных соединений (непериодическая сеть). Можно использовать ту же сеть, что и в Simulation with Concurrent Inputs in a Dynamic Network, которая была линейной сетью с выделенной линией задержки на входе:
net = linearlayer([0 1]);
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.IW{1,1} = [1 1];
view(net)

Можно снова симулировать сетевой ответ на импульсный вход и построить его:
a = net(p); stem(cell2mat(a))

Реакция динамической сети длится дольше, чем вход импульс. Динамическая сеть имеет память. Его реакция в любой данный момент времени зависит не только от текущего входа, но и от истории входа последовательности. Если сеть не имеет никаких обратных соединений, то только конечное количество истории повлияет на ответ. На этом рисунке можно увидеть, что реакция на импульс длится один временной шаг сверх длительности импульса. Это потому, что выделенная линия задержки на входе имеет максимальную задержку 1.
Теперь рассмотрим простую рекуррентно-динамическую сеть, показанную на следующем рисунке.
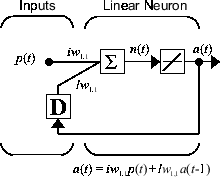
Можно создать сеть, просмотреть ее и симулировать с помощью следующих команд. narxnet команда обсуждается в Design Time Series NARX Feedback Neural Networks.
net = narxnet(0,1,[],'closed');
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.LW{1} = .5;
net.IW{1} = 1;
view(net)

Следующие команды строят график сетевого отклика.
a = net(p); stem(cell2mat(a))

Заметьте, что рекуррентно-динамические сети обычно имеют более длительный ответ, чем сети с прямой связью. Для линейных сетей динамические сети с прямой связью называются конечной импульсной характеристикой (КИХ), потому что реакция на импульсный вход станет нулем после конечного количества времени. Линейные рекуррентно-динамические сети называются бесконечной импульсной характеристикой (БИХ), потому что реакция на импульс может распадаться до нуля (для стабильной сети), но она никогда не станет точно равной нулю. Импульсная характеристика для нелинейной сети не может быть задана, но идеи конечных и бесконечных откликов действительно переносятся.
Динамические сети в целом мощнее статических (хотя и несколько труднее обучаться). Поскольку динамические сети имеют память, они могут быть обучены изучению последовательных или изменяющихся во времени шаблонов. Это имеет приложения в таких разрозненных областях, как предсказание на финансовых рынках [RoJa96], выравнивание канала в системах связи [FeTS03], обнаружение фазы в степень системах [KaGr96], сортировка [JaRa04], обнаружение отказа [ChDa99], распознавание речи [Robin94 Вы можете найти обсуждение многих других динамических сетевых приложений в [MeJa00].
Одно из основных применений динамических нейронных сетей - в системах управления. Это приложение подробно обсуждается в Neural Network Control Systems. Динамические сети также хорошо подходят для фильтрации. Вы увидите использование некоторых линейных динамических сетей для фильтрации, и некоторые из этих идей расширены в этой теме, используя нелинейные динамические сети.
Программное обеспечение Deep Learning Toolbox™ предназначено для обучения класса сети под названием Ledered Digital Dynamic Network (LDDN). Любая сеть, которая может быть организована в форме LDDN, может быть обучена с помощью тулбокса. Вот базовое описание LDDN.
Каждый слой в LDDN состоит из следующих частей:
Набор весовых матриц, которые поступают в тот слой (который может соединяться с других слоев или с внешних входов), связанное правило весовой функции, используемое для объединения весовой матрицы с ее входом (обычно стандартное матричное умножение, dotprod) и связанная с ним разнесенная линия задержки
Вектор смещения
Правило входной функции сети, которое используется для объединения выходов различных весовых функций с смещением для создания входного входа сети (обычно суммирующего соединения, netprod)
Передаточная функция
Сеть имеет входы, которые соединяются со специальными весами, называемыми входными весами и обозначаемыми IWi,j (net.IW{i,j} в коде), где j обозначает число входного вектора, который входит в вес, и i обозначает количество слоя, с которым соединяется вес. Веса, соединяющие один слой с другим, называются весами слоев и обозначаются LWi,j (net.LW{i,j} в коде), где j обозначает количество слоя, приходящего в вес и i обозначает количество слоя на выходе веса.
Следующий рисунок является примером трехуровневого LDDN. Первый слой имеет три связанных с ним веса: один входной вес, вес слоя от слоя 1 и вес слоя от слоя 3. Эти два слоя имеют линии задержки, сопоставленные с ними.
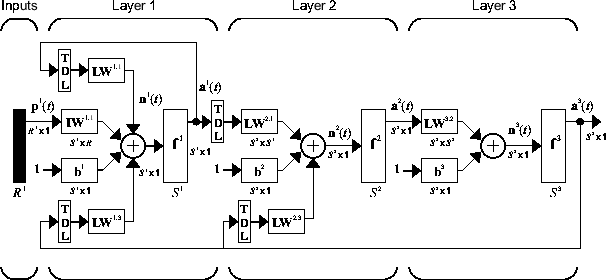
Программное обеспечение Deep Learning Toolbox может использоваться для обучения любого LDDN, при условии, что функции веса, функции входа сети и передаточные функции имеют производные. Большинство известных динамических сетевых архитектур могут быть представлены в форме LDDN. В оставшейся части этой темы вы увидите, как использовать некоторые простые команды для создания и обучения нескольких очень мощных динамических сетей. Другие сети LDDN, не охваченные этой темой, могут быть созданы с помощью типовой команды network, как объяснено в Define Shallow Neural Network Architures.
Динамические сети обучаются в программном обеспечении Deep Learning Toolbox с помощью тех же основанных на градиенте алгоритмов, которые были описаны в Multilayer Shallow Neural Networks and Backpropagation Training. Вы можете выбрать из любой из функций обучения, которые были представлены в этой теме. Примеры приведены в следующих разделах.
Хотя динамические сети могут быть обучены с помощью тех же основанных на градиенте алгоритмов, которые используются для статических сетей, эффективность алгоритмов в динамических сетях может быть довольно различной, и градиент должен быть вычислен более комплексным способом. Снова рассмотрим простую повторяющуюся сеть, показанную на этом рисунке.

Веса имеют два разных эффекта на выходе сети. Первый является прямым эффектом, потому что изменение веса вызывает немедленное изменение выхода на текущем временном шаге. (Этот первый эффект может быть вычислен с помощью стандартного обратного распространения.) Второй эффект является косвенным, потому что некоторые входные входы слоя, такие как a (t − 1), также являются функциями весов. Чтобы учесть этот косвенный эффект, необходимо использовать динамическое обратное распространение для вычисления градиентов, что является более интенсивным в вычислительном отношении. (См. [DeHa01a], [DeHa01b] и [DeHa07].) Ожидайте, что динамическая обратная реализация займет больше времени для обучения, отчасти по этой причине. В сложение поверхности ошибок для динамических сетей могут быть более комплексными, чем для статических сетей. Обучение с большей вероятностью окажется в ловушке местных минимумов. Это говорит о том, что вам может потребоваться несколько раз обучить сеть, чтобы достичь оптимального результата. Некоторые обсуждения по вопросам обучения динамических сетей см. в разделах [DHH01] и [HDH09].
В остальных разделах этой темы показано, как создать, обучить и применить определенные динамические сети к проблемам моделирования, обнаружения и прогнозирования. Некоторые из сетей требуют динамического обратного распространения для вычисления градиентов, а другие - нет. Как пользователь, вам не нужно решать, требуется ли динамическое обратное распространение. Это определяется автоматически программным обеспечением, которое также принимает решение о наилучшей форме динамического обратного распространения для использования. Вам просто нужно создать сеть, а затем обратиться к стандарту train команда.