Чтобы увидеть примеры использования сетей NARX, применяемых в разомкнутый контур форме, системе с обратной связью и многостадийном предсказании без обратной связи, см. Multistep Neural Network Prediction.
Все конкретные динамические сети, обсуждавшиеся до сих пор, были либо сфокусированы на сетях, с динамикой только на вход слоя, либо сети прямого распространения. Нелинейная авторегрессивная сеть с экзогенными входами (NARX) является рекуррентной динамической сетью с соединениями обратной связи, охватывающими несколько слоев сети. Модель NARX основана на линейной модели ARX, которая обычно используется в моделировании timeseries.
Определяющее уравнение для модели NARX
где следующее значение зависимого выходного сигнала y (t) регрессировано на предыдущих значениях выходного сигнала и предыдущих значениях независимого (экзогенного) входного сигнала. Можно реализовать модель NARX с помощью нейронной сети с feedforward, чтобы аппроксимировать f функции. Схема получившейся сети показана ниже, где для приближения используется 2-х слойная сеть прямого распространения. Эта реализация также допускает векторную модель ARX, где вход и выход могут быть многомерными.
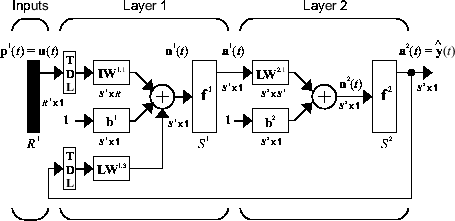
Существует много приложений для сети NARX. Он может использоваться как предиктор, чтобы предсказать следующее значение входного сигнала. Он также может использоваться для нелинейной фильтрации, в которой целевой выход является бесшумной версией входного сигнала. Использование сети NARX показано в другом важном приложении, моделировании нелинейных динамических систем.
Прежде чем показывать обучение сети NARX, важное строение, которая полезна в обучении, нуждается в объяснении. Можно считать выход сети NARX оценкой выхода некоторой нелинейной динамической системы, которую вы пытаетесь смоделировать. Выход подается назад на вход нейронной сети с feedforward как часть стандартной архитектуры NARX, как показано на левом рисунке ниже. Поскольку истинный выход доступен во время обучения сети, можно создать последовательную параллельную архитектуру (см. [NaPa91]), в которой истинный выход используется вместо обратной передачи предполагаемого выхода, как показано на правом рисунке ниже. Это имеет два преимущества. Первый заключается в том, что вход в сеть прямого распространения является более точным. Второе заключается в том, что получившаяся сеть имеет чистую архитектуру прямого распространения, и для обучения может использоваться статическое обратное распространение.
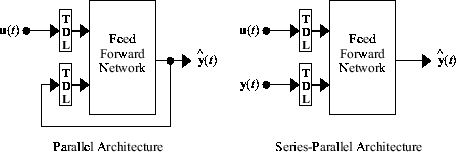
Ниже показано использование последовательной параллельной архитектуры для настройки сети NARX для моделирования динамической системы.
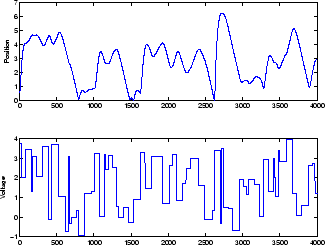
Примером сети NARX является система магнитной левитации, описанная начиная с использования блока NARMA-L2 Controller. Нижний график на следующем рисунке показывает напряжение, приложенное к электромагниту, а верхний график показывает положение постоянного магнита. Данные собирали с интервалом дискретизации 0,01 секунды, чтобы сформировать два временных рядов.
Цель состоит в том, чтобы разработать модель NARX для этой магнитной системы левитации.
Во-первых, загрузите обучающие данные. Используйте выделенные линии задержки с двумя задержками как для входа, так и для выхода, поэтому обучение начинается с третьей точки данных. Существует два входа в последовательно-параллельную сеть, u (t) последовательность и y (t) последовательность.
load magdata
y = con2seq(y);
u = con2seq(u);
Создайте последовательно параллельную сеть NARX с помощью функции narxnet. Используйте 10 нейронов в скрытом слое и используйте trainlm для функции обучения, а затем подготовьте данные с preparets:
d1 = [1:2];
d2 = [1:2];
narx_net = narxnet(d1,d2,10);
narx_net.divideFcn = '';
narx_net.trainParam.min_grad = 1e-10;
[p,Pi,Ai,t] = preparets(narx_net,u,{},y);
(Заметьте, что y последовательность рассматривается как сигнал обратной связи, который является входом, который также является выходом (целевым). Позже, когда вы закроете цикл, соответствующий выход будет подключен к соответствующему входу.) Теперь вы готовы обучать сеть.
narx_net = train(narx_net,p,t,Pi);
Теперь можно симулировать сеть и построить график получившихся ошибок для последовательной параллельной реализации.
yp = sim(narx_net,p,Pi); e = cell2mat(yp)-cell2mat(t); plot(e)

Можно увидеть, что ошибки очень маленькие. Однако из-за последовательного параллельного строения это ошибки только для предсказания с одним шагом вперед. Более строгим тестом было бы переставить сеть в исходную параллельную форму (замкнутый цикл), а затем выполнить итерационное предсказание на многих временных шагах. Теперь показана параллельная операция.
Существует функция тулбокса (closeloop) для преобразования сетей NARX (и других) из последовательно-параллельного строения (разомкнутого контура), которая полезна для обучения, в параллельное строение (замкнутый цикл), которая полезна для многоэтапного предсказания. Следующая команда иллюстрирует, как преобразовать сеть, которую вы только что обучили, в параллельную форму:
narx_net_closed = closeloop(narx_net);
Чтобы увидеть различия между двумя сетями, можно использовать команду view:
view(narx_net)

view(narx_net_closed)

Все обучение проводится в разомкнутом контуре (также называемом последовательно-параллельной архитектурой), включая шаги валидации и тестирования. Типичный рабочий процесс состоит в том, чтобы полностью создать сеть в разомкнутом контуре, и только когда она была обучена (которая включает шаги валидации и тестирования), она преобразуется в замкнутый цикл для многостадийного предсказания. Аналогично, R значения в графический интерфейс пользователя вычисляются на основе результатов обучения без разомкнутого контура.
Теперь можно использовать строение с обратной связью (параллельную), чтобы выполнить итерационное предсказание 900 временных шагов. В этой сети вам нужно загрузить два начальных входа и два начальных выхода в качестве начальных условий. Вы можете использовать preparets функция для подготовки данных. Он будет использовать структуру сети, чтобы определить, как разделить и сдвинуть данные соответствующим образом.
y1 = y(1700:2600);
u1 = u(1700:2600);
[p1,Pi1,Ai1,t1] = preparets(narx_net_closed,u1,{},y1);
yp1 = narx_net_closed(p1,Pi1,Ai1);
TS = size(t1,2);
plot(1:TS,cell2mat(t1),'b',1:TS,cell2mat(yp1),'r')

Рисунок иллюстрирует итерационное предсказание. Синяя линия является фактическим положением магнита, а красная - положением, предсказанным нейронной сетью NARX. Несмотря на то, что сеть предсказывает 900 временных шагов вперед, предсказание очень точно.
В порядок, чтобы параллельный ответ (итерационное предсказание) был точным, важно, чтобы сеть была обучена так, чтобы ошибки в последовательном параллельном строении (одноэтапное предсказание) были очень маленькими.
Можно также создать параллельную (закрытый цикл) сеть NARX, используя narxnet команда с четвертым входным параметром, установленным на 'closed', и обучите эту сеть непосредственно. Как правило, обучение занимает больше времени, и полученная эффективность не так хороша, как полученная при последовательной параллельной подготовке.
Каждый раз, когда нейронная сеть обучается, может привести к другому решению из-за различных начальных значений веса и смещения и различных делений данных в наборы для обучения, валидации и тестирования. В результате различные нейронные сети, обученные одной и той же задаче, могут выдавать различные выходы для одного и того же входа. Чтобы убедиться, что нейронная сеть с хорошей точностью была найдена, переобучите несколько раз.
Существует несколько других методов улучшения начальных решений, если желательна более высокая точность. Для получения дополнительной информации см. «Улучшение обобщения неглубокой нейронной сети» и «Избегайте избыточного оснащения».
Пример маглева показал, как смоделировать временные ряды с одним внешним входным значением с течением времени. Но сеть NARX будет работать для проблем с несколькими внешними входными элементами и предсказывать серии с несколькими элементами. В этих случаях вход и цель состоят из массивов ячеек строк, представляющих время, но с каждым элементом камеры N-by-1 вектор для N элементы входного или целевого сигнала.
Например, вот набор данных, который состоит из 2-х элементных внешних переменных, предсказывающих ряд с 1 элементом.
[X,T] = ph_dataset;
Внешние входы X форматированы как строка массив ячеек из 2-элементных векторов, причем каждый вектор представляет поток кислоты и решения основания. Мишени представляют полученный рН решения с течением времени.
Можно переформатировать собственные многоэлементные последовательные данные из матричной формы в форму временного timeseries нейронной сети с функцией con2seq.
Процесс обучения сети протекает так, как это было сделано выше для задачи маглева.
net = narxnet(10);
[x,xi,ai,t] = preparets(net,X,{},T);
net = train(net,x,t,xi,ai);
y = net(x,xi,ai);
e = gsubtract(t,y); Чтобы увидеть примеры использования сетей NARX, применяемых в разомкнутый контур форме, системе с обратной связью и многостадийном предсказании без обратной связи, см. Multistep Neural Network Prediction.