Нейронные сети обучения Вектора квантования (LVQ)

Архитектура

Архитектура сети LVQ показана ниже.

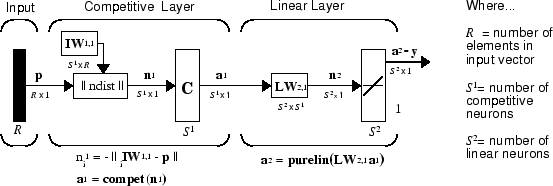
Сеть LVQ имеет первый конкурентный слой и второй линейный слой. Конкурентный слой учится классифицировать входные векторы почти так же, как и конкурентные слои кластер с самоорганизующейся Map Neural Network, описанные в этой теме. Линейный слой преобразует классы конкурентного слоя в целевые классификации, заданные пользователем. Классы, выученные конкурентным слоем, называются подклассами, а классы линейного слоя - целевыми классами.

Как конкурентный, так и линейный слои имеют по одному нейрону на (под- или целевой) класс. Таким образом, конкурентный слой может научиться до S¹ подклассы. Они, в свою очередь, объединяются линейным слоем с образованием S² целевые классы. (S¹ всегда больше S².)

Например, предположим, что нейроны 1, 2 и 3 в конкурентном слое все изучают подклассы входного пространства, которое принадлежит линейному слою целевого класса 2. Тогда конкурентоспособные нейроны 1, 2 и 3 будут иметь LW^2,1веса 1,0 к нейрону n² в линейном слое и весах 0 для всех других линейных нейронов. Таким образом, линейный нейрон производит 1, если любой из трех конкурентоспособных нейронов (1, 2 или 3) выигрывает конкуренцию и выводит 1. Так подклассы конкурентного слоя объединяются в целевые классы в линейном слое.

Короче говоря, 1 в i-й строке a¹ (остальное к элементам массива¹ будет нулем) эффективно выбирает i-й столбец LW^2,1 как выход сети. Каждый такой столбец содержит один 1, соответствующий определенному классу. Таким образом, подкласс 1s из слоя 1 помещается в различные классы LW^2,1a¹ умножение в слое 2.

Вы заранее знаете, какую долю нейронов слоя 1 следует классифицировать в различные выходные выходы класса слоя 2, так что можно задать элементы LW^2,1 в начале. Однако вы должны пройти процедуру обучения, чтобы получить первый слой, чтобы создать правильный выход подкласса для каждого вектора набора обучающих данных. Этот тренинг обсуждается в разделе «Обучение». Сначала рассмотрим, как создать исходную сеть.

Создание сети LVQ

Вы можете создать сеть LVQ с функцией lvqnet,

net = lvqnet(S1,LR,LF)

где

S1 - количество скрытых нейронов первого слоя.
LR - скорость обучения (по умолчанию 0,01).
LF - функция обучения (по умолчанию это learnlv1).

Предположим, что у вас есть 10 входных векторов. Создайте сеть, которая присваивает каждый из этих входных векторов одному из четырех подклассов. Таким образом, в первом конкурентном слое четыре нейрона. Эти подклассы затем назначаются одному из двух выходных классов двумя нейронами в слое 2. Входные векторы и цели заданы

P = [-3 -2 -2 0 0 0 0 2 2 3; 0 1 -1 2 1 -1 -2 1 -1 0];

Tc = [1 1 1 2 2 2 2 1 1 1];

Это может помочь показать детали того, что вы получаете из этих двух строк кода.

P,Tc
P =
    -3    -2    -2     0     0     0     0     2     2     3
     0     1    -1     2     1    -1    -2     1    -1     0
Tc =
     1     1     1     2     2     2     2     1     1     1

График входных векторов следующий.

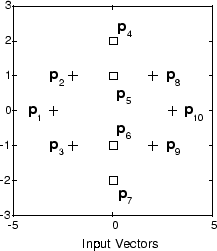
Как видим, существует четыре подкласса входа векторов. Вы хотите, чтобы сеть, которая классифицирует p1, p2, p3, p8, p9 и p10, выдала выход 1, и которая классифицирует векторы p4, p5, p6 и p7, чтобы получить выход 2. Обратите внимание, что эта задача нелинейно разделима, и поэтому не может быть решена перцептроном, но сеть LVQ не имеет никаких трудностей.

Далее преобразуйте Tc матрица к целевым векторам.

T = ind2vec(Tc);

Это дает разреженную матрицу T который может быть отображен полностью с

targets = full(T)

который дает

targets =
     1     1     1     0     0     0     0     1     1     1
     0     0     0     1     1     1     1     0     0     0

Это выглядит правильно. В нем говорится, например, что если у вас есть первый столбец P в качестве входных данных вы должны получить первый столбец targets как выход; и этот выход говорит, что вход падает в классе 1, что правильно. Теперь вы готовы позвонить lvqnet.

Функции lvqnet создать сеть с четырьмя нейронами.

net = lvqnet(4);

Сконфигурируйте и подтвердите, что начальные значения матрицы веса первого уровня инициализируются средней точкой функции значениями в центре области значений входных данных.

net = configure(net,P,T);
net.IW{1}
ans =
     0     0
     0     0
     0     0
     0     0

Подтвердите, что веса второго слоя имеют 60% (6 из 10 в Tc) его столбцов с 1 в первой строке, (соответствующий классу 1), и 40% его столбцов имеют 1 во второй строке (соответствующий классу 2). С четырьмя столбцами, 60% и 40% фактически округлятся до 50%, и в каждой строке есть два 1.

net.LW{2,1}
ans =
     1     1     0     0
     0     0     1     1

Это тоже имеет смысл. В нем говорится, что, если конкурентный слой создает 1 как первый или второй элемент, входной вектор классифицируется как класс 1; в противном случае это класс 2.

Можно заметить, что первые два конкурентоспособных нейрона связаны с первым линейным нейроном (с весами 1), в то время как вторые два конкурентных нейрона связаны со вторым линейным нейроном. Все другие веса между конкурирующими нейронами и линейными нейронами имеют значения 0. Таким образом, каждый из двух целевых классов (линейные нейроны) является, по сути, объединением двух подклассов (конкурентных нейронов).

Можно симулировать сеть с sim. Используйте исходную P матрица как вход, чтобы увидеть, что вы получаете.

Y = net(P);
Yc = vec2ind(Y)
Yc =
     1     1     1     1     1     1     1     1     1     1

Сеть классифицирует все входы в класс 1. Поскольку это не то, что вы хотите, вы должны обучить сеть (корректировка только весов слоя 1), прежде чем вы можете ожидать хорошего результата. В следующих двух разделах рассматриваются два правила обучения LVQ и процесс обучения.

LVQ1 правила обучения (learnlv1)

Обучение LVQ на конкурентном слое основано на наборе входных/целевых пар.

${p_{1}, t_{1}}, {p_{2}, t_{2}}, \dots {p_{Q}, t_{Q}}$

Каждый целевой вектор имеет один 1. Остальные его элементы 0. Значение 1 сообщает правильную классификацию связанного входа. Например, рассмотрите следующую пару обучения.

${p_{1} = [\begin{matrix} 2 \\ - 1 \\ 0 \end{matrix}], t_{1} = [\begin{array}{l} 0 \\ 0 \\ 1 \\ 0 \end{array}]}$

Здесь существуют входные векторы трех элементов, и каждый входной вектор должен быть присвоен одному из четырех классов. Сеть должна быть обучена так, чтобы она классифицировала входной вектор, показанный выше, в третий из четырех классов.

Для обучения сети представлен вектор входа p и расстояние от p до каждой строки входа матрицы веса IW^1,1 вычисляется функцией negdist. Скрытые нейроны слоя 1 конкурируют. Предположим, что i-й элемент n¹ наиболее положителен, и нейрон i * выигрывает конкурс. Затем конкурентная передаточная функция создает 1 как i * й элемент массива¹. Все другие элементы массива¹ 0.

Когда¹ умножается на слой 2 веса LW^2,1, сингл 1 в a¹ выбирает класс k *, сопоставленный с входом. Таким образом, сеть присвоила входной вектор p классу k * и α²_k * будет равен 1. Конечно, это назначение может быть хорошим или плохим, поскольку _tk* может быть 1 или 0, в зависимости от того, принадлежал ли вход классу k * или нет.

Отрегулируйте i * -ю строку IW^1,1 таким образом переместить эту строку ближе к вектору входа p, если назначение верно, и отодвинуть строку от p, если назначение неправильно. Если p классифицировано правильно,

$(α_{k *}^{2} = t_{k *} = 1)$

вычислить новое значение i * й строки IW^1,1 как

${}_{i *}I W^{1, 1} (q) = {}_{i *}I W^{1, 1} (q - 1) + α (p (q) - {}_{i *}I W^{1, 1} (q - 1))$

С другой стороны, если p классифицировано неправильно,

$(α_{k *}^{2} = 1 \neq t_{k *} = 0)$

вычислить новое значение i * й строки IW^1,1 как

${}_{i *}I W^{1, 1} (q) = {}_{i *}I W^{1, 1} (q - 1) - α (p (q) - {}_{i *}I W^{1, 1} (q - 1))$

Можно внести эти коррекции в i * -ю строку IW^1,1 автоматически, без влияния на другие строки IW^1,1, путем обратного распространения ошибок выхода на слой 1.

Такие коррекции перемещают скрытый нейрон к векторам, которые попадают в класс, для которого он образует подкласс, и вдали от векторов, которые попадают в другие классы.

Функция обучения, которая реализует эти изменения в весах слоя 1 в сетях LVQ, learnlv1. Его можно применять во время обучения.

Обучение

Далее вам нужно обучить сеть, чтобы получить веса первого слоя, которые приводят к правильной классификации входа векторов. Вы делаете это с train как со следующими командами. Во-первых, установите эпоху обучения равной 150. Затем используйте train:

net.trainParam.epochs = 150;
net = train(net,P,T);

Теперь подтвердите веса первого слоя.

net.IW{1,1}
ans =
    0.3283    0.0051
   -0.1366    0.0001
   -0.0263    0.2234
         0   -0.0685

Следующий график показывает, что эти веса переместились в свои соответствующие классификационные группы.

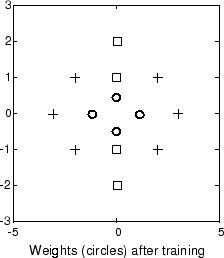
Чтобы подтвердить, что эти веса действительно приводят к правильной классификации, возьмите матрицу P как вход и моделирование сети. Затем посмотрите, какие классификации производятся сетью.

Y = net(P);
Yc = vec2ind(Y)

Это дает

Yc =
     1     1     1     2     2     2     2     1     1     1

что ожидается. В качестве последней проверки попробуйте вход, близкий к вектору, который использовался в обучении.

pchk1 = [0; 0.5];
Y = net(pchk1);
Yc1 = vec2ind(Y)

Это дает

Yc1 =
     2

Это выглядит правильно, потому что pchk1 близок к другим векторам, классифицированным как 2. Точно так же,

pchk2 = [1; 0];
Y = net(pchk2);
Yc2 = vec2ind(Y)

дает

Yc2 =
     1

Это тоже выглядит правильно, потому что pchk2 близок к другим векторам, классифицированным как 1.

Можно хотеть попробовать пример программы Learning Vector Quantization. Это следует за обсуждением обучения, приведенным выше.

Дополнительное правило LVQ2.1 обучения (learnlv2)

Следующее правило обучения может быть применено после первого применения LVQ1. Это может улучшить результат первого обучения. Эта конкретная версия LVQ2 (упоминается как LVQ2.1 в литературе [Koho97]) воплощена в функции learnlv2. Еще раз обратите внимание, что LVQ2.1 должно использоваться только после применения LVQ1.

Обучение здесь подобно тому, что в learnlv2 за исключением двух векторов слоя 1, которые являются ближайшими к входному вектору, могут быть обновлены при условии, что один принадлежит правильному классу, а один принадлежит неправильному классу, и далее при условии, что вход падает в «окно» около средней платы двух векторов.

Окно определяется как

$\min (\frac{d_{i}}{d_{j}}, \frac{d_{j}}{d_{i}}) > s$

где

$s \equiv \frac{1 - w}{1 + w}$

(где _di и _dj являются евклидовыми расстояниями p от _i * IW^1,1 и _j * IW^1,1, соответственно). Примите значение для w в области значений от 0,2 до 0,3. Если вы выбираете, например, 0,25, то s = 0,6. Это означает, что, если минимум двух коэффициентов расстояния больше 0,6, два вектора корректируются. То есть, если вход находится вблизи средней платы, отрегулируйте два вектора, при условии, что входной вектор p и _j * IW^1,1 относятся к одному и тому же классу, и p и _i * IW^1,1 не принадлежат к одному и тому же классу.

Внесенные корректировки

${}_{i *}I W^{1, 1} (q) = {}_{i *}I W^{1, 1} (q - 1) - α (p (q) - {}_{i *}I W^{1, 1} (q - 1))$

${}_{j *}I W^{1, 1} (q) = {}_{j *}I W^{1, 1} (q - 1) + α (p (q) - {}_{j *}I W^{1, 1} (q - 1))$

Таким образом, учитывая два вектора, ближайших к входу, пока один принадлежит неправильному классу, а другой - правильному классу, и пока вход падает в окне средней платы, два вектора корректируются. Такая процедура позволяет вектору, который просто едва ли классифицирован правильно с LVQ1, перемещаться еще ближе к входу, поэтому результаты более устойчивы.

Функция	Описание
`competlayer`	Создайте слой конкуренции.
`learnk`	Правила обучения Кохонен.
`selforgmap`	Создайте самоорганизующуюся карту.
`learncon`	Функция обучения смещением совести.
`boxdist`	Расстояние между двумя векторами положения.
`dist`	Евклидова функция веса расстояния.
`linkdist`	Функция расстояния ссылки.
`mandist`	Функция веса расстояния Манхэттена.
`gridtop`	Функция топологии слоя сетки.
`hextop`	Шестиугольная функция топологии слоя.
`randtop`	Функция топологии случайного слоя.
`lvqnet`	Создайте сеть квантования вектора обучения.
`learnlv1`	LVQ1 функции обучения весу.
`learnlv2`	LVQ2 функции обучения весу.

Документация