Самоорганизующиеся карты функций (SOFM) учатся классифицировать входные векторы согласно тому, как они сгруппированы во входном пространстве. Они отличаются от конкурентных слоев тем, что соседние нейроны в самоорганизующейся карте учатся распознавать соседние участки входного пространства. Таким образом, самоорганизующиеся карты изучают как распределение (как и конкурентные слои), так и топологию входных векторов, на которых они обучаются.
Нейроны в слое SOFM расположены первоначально в физических положениях согласно функции топологии. Функция gridtop, hextop, или randtop может расположить нейроны в сетке, шестиугольной или случайной топологии. Расстояния между нейронами вычисляются из их положений с функцией расстояния. Существует четыре функции расстояния, dist, boxdist, linkdist, и mandist. Расстояние ссылки является наиболее распространенным. Эти функции топологии и расстояния описаны в Topologies (gridtop, hextop, randtop) и Distance Functions (dist, linkdist, mandist, boxdist).
Здесь сеть карты самоорганизующихся функций идентифицирует i нейронов *, используя ту же процедуру, что и используемый конкурентным слоем. Однако вместо обновления только нейрона-победителя все нейроны в определенном районе Ni * (d) нейрона-победителя обновляются, используя правило Кохонена. В частности, все такие нейроны i ∊ Ni * (d) корректируются следующим образом:
или
Здесь соседство Ni * (d) содержит индексы для всех нейронов, которые лежат в радиусе d выигрывающего нейрона i *.
Таким образом, когда представлен вектор p, веса нейрона-победителя и его близких соседей движутся к p. Следовательно, после многих презентаций соседние нейроны научились векторам, подобным друг другу.
Другая версия обучения SOFM, называемая пакетным алгоритмом, представляет весь набор данных в сеть до обновления весов. Затем алгоритм определяет выигрышный нейрон для каждого входного вектора. Затем каждый вектор веса переходит в среднее положение всех входных векторов, для которых он является победителем или для которых он находится по соседству с победителем.
Чтобы проиллюстрировать концепцию микрорайонов, рассмотрим рисунок ниже. Левая схема показывает двумерную окрестность радиуса d = 1 вокруг нейрона 13. Правая схема показывает окрестность радиуса d = 2.
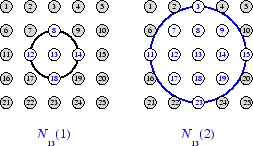
Эти кварталы могут быть записаны как N 13 (1) = {8, 12, 13, 14, 18} и
<reservedrangesplaceholder0> 13 (2) = {3, 7, 8, 9, 11, 12, 13, 14, 15, 17, 18, 19, 23}.
Нейроны в SOFM не должны быть расположены в двумерном шаблоне. Можно использовать одномерное расположение, или три или более размерности. Для одномерного SOFM нейрон имеет только два соседа в радиусе 1 (или один соседний, если нейрон находится в конце линии). Можно также задать расстояние различными способами, например, с помощью прямоугольных и шестиугольных расположений нейронов и окрестностей. Эффективность сети не чувствительна к точной форме кварталов.
gridtop, hextop, randtop)Можно задать различные топологии для исходных расположений нейронов с функциями gridtop, hextop, и randtop.
gridtop топология начинается с нейронов в прямоугольной сетке, подобной той, которая показана на предыдущем рисунке. Например, предположим, что вы хотите массив 2 на 3 из шести нейронов. Вы можете получить это с
pos = gridtop([2, 3])
pos =
0 1 0 1 0 1
0 0 1 1 2 2
Здесь нейрон 1 имеет положение (0,0), нейрон 2 имеет положение (1,0), а нейрон 3 имеет положение (0,1) и т.д.
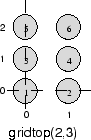
Обратите внимание, что вы попросили о gridtop с размерностью размерами назад, вы бы получили несколько другое расположение:
pos = gridtop([3, 2])
pos =
0 1 2 0 1 2
0 0 0 1 1 1
Можно создать набор нейронов 8 на 10 в gridtop топология со следующим кодом:
pos = gridtop([8 10]); plotsom(pos)

Как показано, нейроны в gridtop топология действительно лежит на сетке.
hextop функция создает подобный набор нейронов, но они имеют шестиугольный шаблон. Шаблон 2 на 3 из hextop нейроны генерируются следующим образом:
pos = hextop([2, 3])
pos =
0 1.0000 0.5000 1.5000 0 1.0000
0 0 0.8660 0.8660 1.7321 1.7321
Обратите внимание, что hextop является шаблоном по умолчанию для сетей SOM, сгенерированных с selforgmap.
Можно создать и построить график набора нейронов 8 на 10 в hextop топология со следующим кодом:
pos = hextop([8 10]); plotsom(pos)

Обратите внимание на положения нейронов в шестиугольном расположении.
Наконец, randtop функция создает нейроны в N-мерном случайном шаблоне. Следующий код генерирует случайный шаблон нейронов.
pos = randtop([2, 3])
pos =
0 0.7620 0.6268 1.4218 0.0663 0.7862
0.0925 0 0.4984 0.6007 1.1222 1.4228
Можно создать и построить график набора нейронов 8 на 10 в randtop топология со следующим кодом:
pos = randtop([8 10]); plotsom(pos)

Для примеров смотрите справку для этих функций топологии.
dist, linkdist, mandist, boxdist)В этом тулбоксе существует четыре способа вычисления расстояний от конкретного нейрона до его соседей. Каждый метод вычисления реализован со специальной функцией.
dist функция вычисляет евклидовы расстояния от домашнего нейрона до других нейронов. Предположим, у вас есть три нейрона:
pos2 = [0 1 2; 0 1 2]
pos2 =
0 1 2
0 1 2
Вы находите расстояние от каждого нейрона до другого с
D2 = dist(pos2)
D2 =
0 1.4142 2.8284
1.4142 0 1.4142
2.8284 1.4142 0
Таким образом, расстояние от нейрона 1 до самого себя составляет 0, расстояние от нейрона 1 до нейрона 2 составляет 1.4142 и т.д.
На графике ниже показан домашний нейрон в двумерном (gridtop) слой нейронов. Домашний нейрон имеет окрестности увеличивающегося диаметра, окружающие его. Район диаметром 1 включает в себя домашний нейрон и его ближайшие соседи. Окрестность диаметра 2 включает нейроны диаметром 1 и их ближайшие соседи.
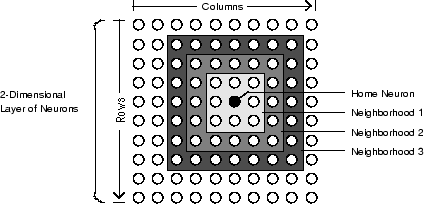
Что касается dist функция, все окрестности для карты слоя S-нейронов представлены матрицей расстояний S-на-S. Конкретные расстояния, показанные выше (1 в непосредственной близости, 2 в окрестности 2 и т.д.), генерируются функцией boxdist. Предположим, что у вас есть шесть нейронов в gridtop строение.
pos = gridtop([2, 3])
pos =
0 1 0 1 0 1
0 0 1 1 2 2
d = boxdist(pos)
d =
0 1 1 1 2 2
1 0 1 1 2 2
1 1 0 1 1 1
1 1 1 0 1 1
2 2 1 1 0 1
2 2 1 1 1 0
Расстояние от нейрона 1 до 2, 3 и 4 составляет всего 1, поскольку они находятся в непосредственной близости. Расстояние от нейрона 1 до обоих 5 и 6 равняется 2. Расстояние от обоих 3 и 4 до всех других нейронов составляет всего 1.
Расстояние ссылки от одного нейрона - это просто количество ссылок или шагов, которые необходимо предпринять, чтобы добраться до рассматриваемого нейрона. Таким образом, если вы вычисляете расстояния от того же набора нейронов с linkdist, вы получаете
dlink =
0 1 1 2 2 3
1 0 2 1 3 2
1 2 0 1 1 2
2 1 1 0 2 1
2 3 1 2 0 1
3 2 2 1 1 0
Расстояние Манхэттена между двумя векторами x и y вычисляется как
D = sum(abs(x-y))
Таким образом, если у вас есть
W1 = [1 2; 3 4; 5 6]
W1 =
1 2
3 4
5 6
и
P1 = [1;1]
P1 =
1
1
тогда вы получите на расстояния
Z1 = mandist(W1,P1)
Z1 =
1
5
9
Расстояния, рассчитанные с mandist действительно следуйте математическому выражению, приведенному выше.
Архитектура для этого SOFM показана ниже.
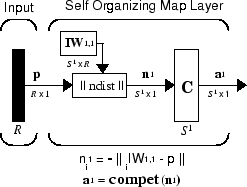
Эта архитектура подобна архитектуре конкурирующей сети, кроме случаев, когда здесь не используется никакого смещения. Конкурентная передаточная функция создает элемент 1 для выхода a1i , соответствующий i *, нейрону-победителю. Все другие выходные элементы в a1 0.
Однако, как описано выше, нейроны, близкие к нейрону-победителю, обновляются вместе с нейроном-победителем. Вы можете выбрать из различных топологий нейронов. Точно так же можно выбрать из различных выражений расстояния, чтобы вычислить нейроны, которые близки к нейрону-победителю.
selforgmap)Вы можете создать новую сеть SOM с функцией selforgmap. Эта функция задает переменные, используемые в двух фазах обучения:
Эти значения используются для обучения и адаптации.
Рассмотрим следующий пример.
Предположим, что вы хотите создать сеть, имеющую входные векторы с двумя элементами, и что вы хотите иметь шесть нейронов в шестигранной сети 2 на 3. Код для получения этой сети:
net = selforgmap([2 3]);
Предположим, что векторы для обучения:
P = [.1 .3 1.2 1.1 1.8 1.7 .1 .3 1.2 1.1 1.8 1.7;...
0.2 0.1 0.3 0.1 0.3 0.2 1.8 1.8 1.9 1.9 1.7 1.8];Можно сконфигурировать сеть, чтобы ввести данные и построить все это с:
net = configure(net,P); plotsompos(net,P)

Зеленые пятна являются векторами обучения. Инициализация для selforgmap распределяет начальные веса по входному пространству. Обратите внимание, что они первоначально находятся на некотором расстоянии от обучающих векторов.
При симуляции сети вычисляются отрицательные расстояния между вектором веса каждого нейрона и вектором входа (negdist), чтобы получить взвешенные входы. Взвешенные входы также являются чистыми входами (netsum). Чистые входы конкурируют (compet) так, что только нейрон с самым положительным входом сети выдаст 1.
learnsomb)Обучение по умолчанию в самоорганизующейся карте функций происходит в пакетном режиме (trainbu). Функция обучения весу для самоорганизующейся карты learnsomb.
Во-первых, сеть идентифицирует выигрышный нейрон для каждого вектора входа. Затем каждый вектор веса переходит в среднее положение всех входных векторов, для которых он является победителем или для которых он находится по соседству с победителем. Расстояние, которое определяет размер окрестности, изменяется во время обучения на двух фазах.
Эта фаза длится в течение заданного количества шагов. Расстояние от области начинается с заданного начального расстояния и уменьшается до расстояния от области настройки (1,0). Когда расстояние между ними уменьшается на этой фазе, нейроны сети обычно упорядочивают себя во входном пространстве с той же топологией, в которой они упорядочены физически.
Эта фаза длится для остальной части обучения или адаптации. Размер окрестности уменьшился ниже 1, поэтому для каждой выборки учится только выигрышный нейрон.
Теперь рассмотрим некоторые конкретные значения, обычно используемые в этих сетях.
Обучение происходит согласно learnsomb параметр обучения, показанный здесь со значением по умолчанию.
Параметр обучения | Значение по умолчанию | Цель |
|---|---|---|
|
| Начальный размер окрестности |
|
| Упорядоченное расположение шагов фазы |
Размер окрестности NS изменяется через две фазы: фазу упорядоченного расположения и фазу настройки.
Фаза упорядоченного расположения длится столько шагов, сколько LP.steps. Во время этой фазы алгоритм настраивает ND от начального размера окрестности LP.init_neighborhood до 1. Именно на этой фазе веса нейронов упорядочиваются во входном пространстве, сопоставимом с соответствующими положениями нейронов.
Во время фазы настройки ND меньше 1. На этой фазе ожидается, что веса будут распределяться относительно равномерно по входному пространству с сохранением их топологического порядка, обнаруженного на фазе упорядоченного расположения.
Таким образом, векторы веса нейрона первоначально делают большие шаги все вместе к области входного пространства, где происходят входные векторы. Затем, когда размер окрестности уменьшается до 1, карта имеет тенденцию упорядочивать себя топологически над представленными входными векторами. Если размер района равен 1, сеть должна быть достаточно хорошо упорядочена. Обучение продолжается в порядок, чтобы дать нейронам время равномерно распределиться по входу векторам.
Как и в случае с конкурентоспособными слоями, нейроны самоорганизующейся карты будут упорядочиваться с приблизительно равными расстояниями между ними, если входные векторы появляются с четной вероятностью на протяжении всего участка входного пространства. Если входные векторы происходят с различной частотой во всем входном пространстве, слой функции map имеет тенденцию выделять нейроны области, пропорциональной частоте входа векторов там.
Таким образом, карты функций, во время обучения классификации их входов, также изучают как топологию, так и распределение их входов.
Вы можете обучить сеть на 1000 эпох с
net.trainParam.epochs = 1000; net = train(net,P); plotsompos(net,P)

Вы можете увидеть, что нейроны начали двигаться к различным группам обучения. Требуется дополнительное обучение, чтобы приблизить нейроны к различным группам.
Как отмечалось ранее, самоорганизующиеся карты отличаются от обычного конкурентного обучения с точки зрения того, какие нейроны обновляют свои веса. Вместо обновления только победителя карты функций обновляют веса победителя и его соседей. Результатом является то, что соседние нейроны, как правило, имеют сходные векторы веса и чувствительны к подобным входным векторам.
Два примера кратко описаны ниже. Можно также попробовать аналогичные примеры Одномерная Самоорганизующаяся Карта и Двумерная Самоорганизующаяся Карта.
Рассмотрим 100 двухэлементных единичных входных векторов, распределенных равномерно между 0 ° и 90 °.
angles = 0:0.5*pi/99:0.5*pi;
Вот график данных.
P = [sin(angles); cos(angles)];
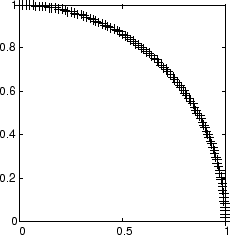
Самоорганизующаяся карта определяется как одномерный слой из 10 нейронов. Эта карта должна быть обучена на этих входных векторах, показанных выше. Первоначально эти нейроны находятся в центре рисунка.
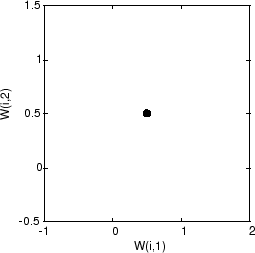
Конечно, потому что все векторы веса начинаются в середине входного векторного пространства, все, что вы видите сейчас, это одна окружность.
Когда обучение начинается, векторы веса перемещаются вместе к входным векторам. Они также становятся упорядоченными, когда размер района уменьшается. Наконец, слой корректирует свои веса так, чтобы каждый нейрон сильно реагировал на область входного пространства, занимаемую входом векторами. Размещение соседних векторов веса нейронов также отражает топологию входных векторов.
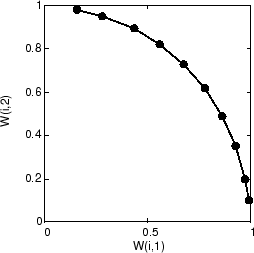
Обратите внимание, что самоорганизующиеся карты обучаются с входом векторами в случайном порядке, поэтому начало с тех же начальных векторов не гарантирует одинаковых результатов обучения.
В этом примере показано, как можно обучить двумерную самоорганизующуюся карту.
Сначала создаются некоторые случайные входные данные со следующим кодом:
P = rands(2,1000);
Вот график из этих 1000 входных векторов.
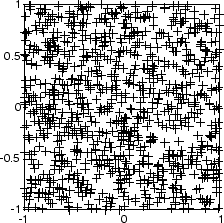
Для классификации этих входных векторов используется двумерная карта 5 на 6 из 30 нейронов. Двумерная карта является пятью нейронами на шесть нейронов с расстояниями, рассчитанными согласно функции соседства расстояния Манхэттена mandist.
Затем карта обучается для 5000 циклов презентации с отображениями каждые 20 циклов.
Вот как выглядит самоорганизующаяся карта после 40 циклов.
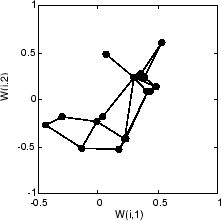
Векторы веса, показанные с кругами, размещены почти случайным образом. Однако даже после всего 40 циклов представления соседние нейроны, соединенные линиями, имеют векторы веса, близкие друг к другу.
Вот карта после 120 циклов.
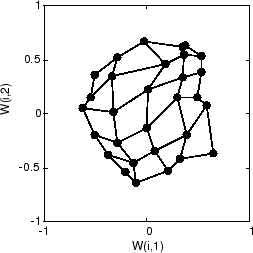
После 120 циклов карта начала организовываться согласно топологии входного пространства, что ограничивает входные векторы.
Следующий график после 500 циклов показывает карту, более равномерно распределенную по входному пространству.
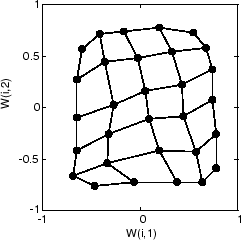
Наконец, после 5000 циклов карта довольно равномерно распределена по входному пространству. В сложение нейроны расположены очень равномерно, отражая четное распределение входа векторов в этой задаче.
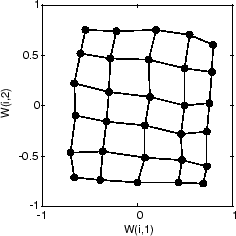
Таким образом, двумерная самоорганизующаяся карта научилась топологии своих входов пространства.
Важно отметить, что хотя самоорганизующаяся карта не занимает много времени, чтобы организовать себя так, чтобы соседние нейроны распознавали подобные входы, может потребоваться много времени, чтобы карта окончательно расположилась согласно распределению входа векторов.
Алгоритм настройки обычно намного быстрее, чем инкрементный алгоритм, и это алгоритм по умолчанию для SOFM-обучения. Вы можете экспериментировать с этим алгоритмом на простом наборе данных со следующими командами:
x = simplecluster_dataset net = selforgmap([6 6]); net = train(net,x);
Эта командная последовательность создает и обучает двумерную карту 6 на 6 из 36 нейронов. Во время обучения появляется следующий рисунок.
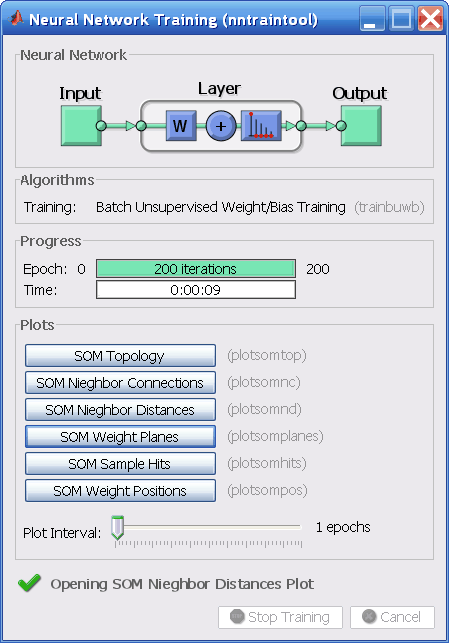
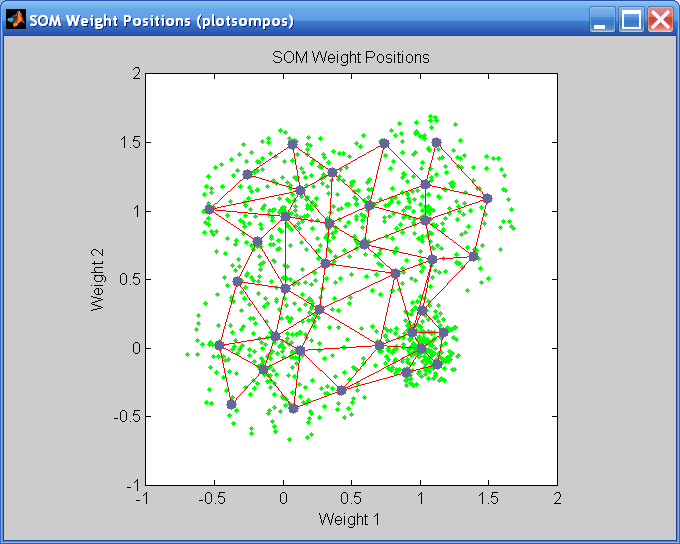
Существует несколько полезных визуализаций, к которым можно получить доступ из этого окна. При нажатии кнопки SOM Weight Positions появляется следующий рисунок, на котором показаны местоположения точек данных и векторов веса. Как показывает рисунок, после всего 200 итераций пакетного алгоритма карта хорошо распределена через входное пространство.
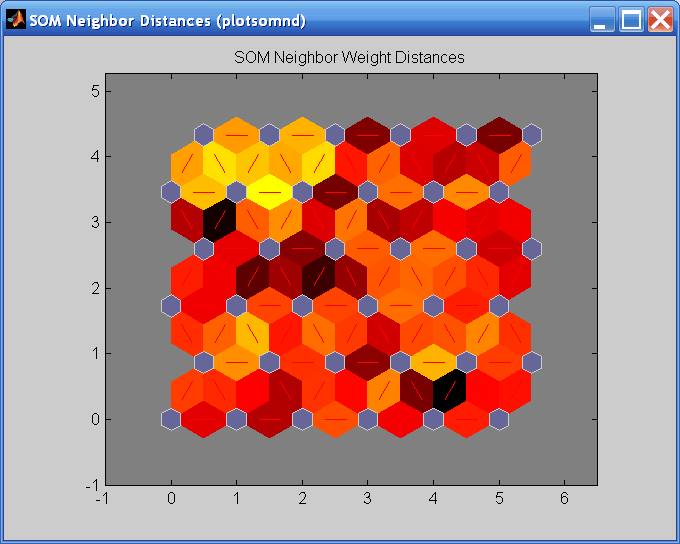
Когда входное пространство имеет высокую размерность, вы не можете визуализировать все веса одновременно. В этом случае выберите SOM Neighbor Distances. Появляется следующий рисунок, которая указывает на расстояния между соседними нейронами.
Этот рисунок использует следующую расцветку:
Голубые шестиугольники представляют нейроны.
Красные линии соединяют соседние нейроны.
Цвета в областях, содержащих красные линии, указывают на расстояния между нейронами.
Более темные цвета представляют большие расстояния.
Более светлые цвета представляют меньшие расстояния.
Группа светлых сегментов появляется в верхней левой области, ограниченной некоторыми более темными сегментами. Эта группировка указывает, что сеть сгруппировала данные в две группы. Эти две группы можно увидеть на предыдущем весовом рисунке. Нижняя правая область этого рисунка содержит небольшую группу тесно кластеризованных точек данных. Соответствующие веса ближе друг к другу в этой области, что обозначено более легкими цветами на рисунке расстояния между соседями. Когда веса в этой маленькой области соединяются с большей областью, расстояния больше, как показано более темной полосой в соседнем рисунке расстояния. Сегменты в нижней правой области рисунка соседнего расстояния темнее, чем сегменты в верхней левой области. Это различие цветов указывает, что точки данных в этой области находятся дальше друг от друга. Это расстояние подтверждено на рисунке положения веса.
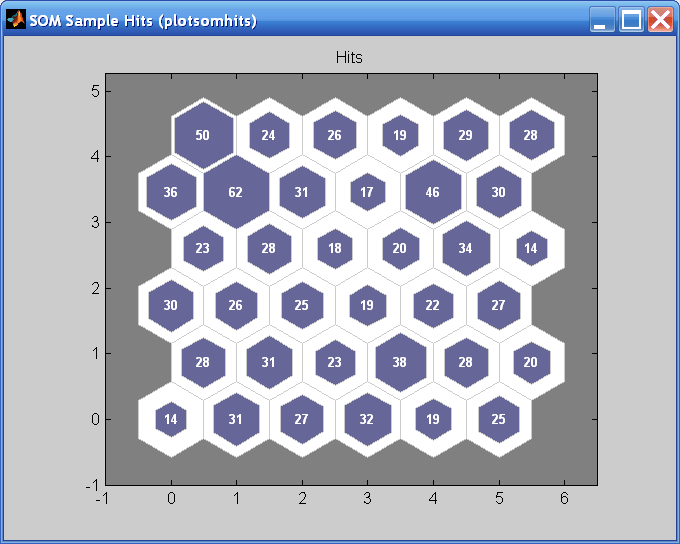
Другой полезный рисунок может сказать, сколько точек данных связано с каждым нейроном. Нажмите SOM Sample Hits, чтобы увидеть следующий рисунок. Лучше всего, если данные довольно равномерно распределены по нейронам. В этом примере данные концентрируются немного больше в лево-верхних нейронах, но в целом распределение довольно равномерно.
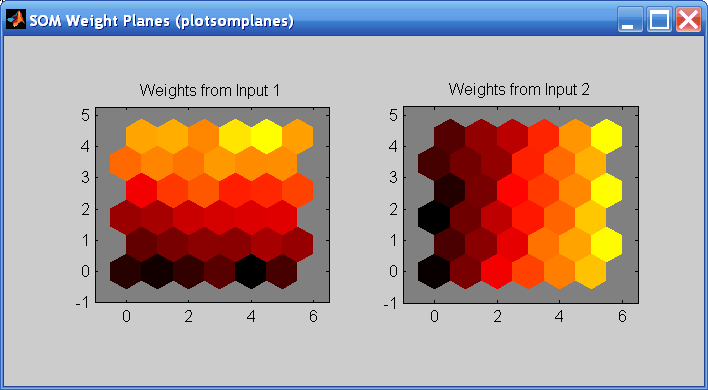
Можно также визуализировать сами веса, используя рисунок весовой плоскости. Нажмите SOM Weight Planes в окне обучения, чтобы получить следующий рисунок. Для каждого элемента входного вектора существует весовая плоскость (два, в данном случае). Это визуализация весов, которые соединяют каждый вход с каждым из нейронов. (Более светлые и темные цвета представляют большие и меньшие веса, соответственно.) Если шаблоны соединений двух входов очень похожи, можно предположить, что входы были сильно коррелированы. В этом случае вход 1 имеет связи, которые сильно отличаются от соединений входа 2.
Можно также создать все предыдущие рисунки из командной строки. Попробуйте следующие команды графического изображения: plotsomhits, plotsomnc, plotsomnd, plotsomplanes, plotsompos, и plotsomtop.