Два или более нейронов, показанных ранее, могут быть объединены в слой, и конкретная сеть может содержать один или более таких слоев. Сначала рассмотрим один слой нейронов.
Следует однослойная сеть с R входными элементами и S нейронами.
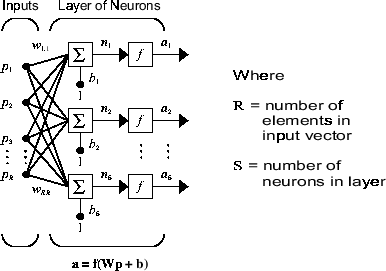
В этой сети каждый элемент входного вектора p соединяется с каждым входом нейрона через матрицу веса W. i-й нейрон имеет лето, которое собирает свои взвешенные входы и смещение, чтобы сформировать свой собственный скалярный выходной n (i). Различные n (i), взятые вместе, образуют входной вектор S-element n. Наконец, выходы нейронного слоя образуют вектор-столбец a. Выражение для a показано в нижней части рисунка.
Обратите внимание, что обычно количество входов в слой отличается от количества нейронов (то есть R не обязательно равно S). Слой не ограничен, чтобы количество его входов равнялось количеству его нейронов.
Можно создать один (композитный) слой нейронов, имеющих различные передаточные функции, просто поместив две из сетей, показанных ранее параллельно. Обе сети будут иметь одинаковые входы, и каждая сеть будет создавать некоторые выходы.
Входные векторные элементы поступают в сеть через весовую матрицу W.
Обратите внимание, что индексы строк элементов матрицы W указывают нейрон назначения веса, а индексы столбцов указывают, какой источник является входом для этого веса. Таким образом, индексы в w 1,2 говорят, что сила сигнала от второго элемента входа к первому (и только) нейрону w 1,2 .
Нейрон S R однослойная сеть также может быть нарисован в сокращенном обозначении.
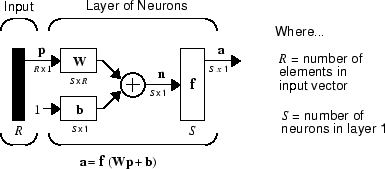
Здесь p - R входной вектор -length, W - S × R матрица, a и b - S -length векторы. Как определено ранее, слой нейронов включает матрицу веса, операции умножения, вектор смещения b, лето и блоки передаточной функции.
Чтобы описать сети, имеющие несколько слоев, обозначение должна быть расширена. В частности, ему нужно провести различие между матрицами веса, которые связаны со входами, и матрицами веса, которые связаны между слоями. Он также должен идентифицировать источник и место назначения для матриц веса.
Мы будем вызывать матрицы веса, связанные с входами входных весов; мы будем вызывать весовые матрицы, соединенные с весами слоев выходов. Кроме того, суперскрипты используются, чтобы идентифицировать источник (второй индекс) и пункт назначения (первый индекс) для различных весов и других элементов сети. Для иллюстрации, однослойная многоуровневая входная сеть, показанная выше, здесь перерисовывается в сокращенном виде.
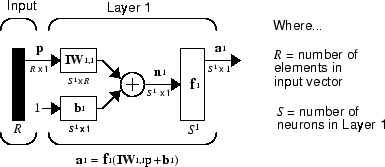
Как видим, матрица веса, соединенная с вектором входа p, помечена как матрица входа веса (IW1,1), имеющий источник 1 (второй индекс) и адресат 1 (первый индекс). Элементы слоя 1, такие как смещение, вход и выход сети, имеют верхний индекс 1, чтобы сказать, что они связаны с первым слоем.
В Нескольких Слоях Нейронов используются матрицы веса слоя (LW), а также матрицы входного веса (IW).
Сеть может иметь несколько слоев. Каждый слой имеет весовую матрицу W, вектор смещения b и вектор выхода A. Чтобы различать весовые матрицы, выходные векторы и т.д., для каждого из этих слоев в рисунки, номер слоя добавляется как верхний индекс к интересующей переменной. Вы можете увидеть использование этого слоя обозначения в трехслойной сети, показанной следующим, и в уравнениях в нижней части рисунка.
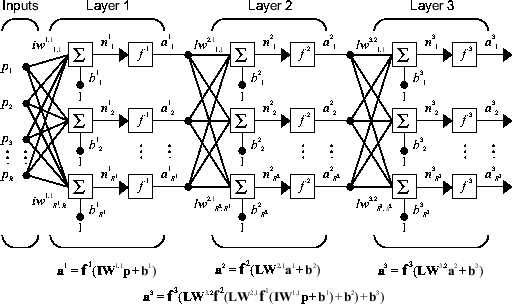
Сеть, показанная выше, имеет R1 входы, S1 нейроны в первом слое, S2 нейроны во втором слое и т.д. Обычно различные слои имеют разное количество нейронов. Постоянный вход 1 подается на смещение для каждого нейрона.
Обратите внимание, что выходы каждого промежуточного слоя являются входами для следующего слоя. Таким образом, слой 2 может быть проанализирован как однослойная сеть с S1 входы, S2 нейроны и S2 × S1 матрица веса W2. Вход для слоя 2 равен1; выходные выходы:2. Теперь, когда все векторы и матрицы слоя 2 были идентифицированы, его можно рассматривать как однослойную сеть самостоятельно. Этот подход можно использовать с любым слоем сети.
Слои многослойной сети играют различные роли. Слой, который создает выход сети, называется выходным слоем. Все другие слои называются скрытыми слоями. Трехслойная сеть, показанная выше, имеет один выходной слой (слой 3) и два скрытых слоя (слой 1 и слой 2). Некоторые авторы ссылаются на входы как на четвертый слой. Этот тулбокс не использует это обозначение.
Архитектура многослойной сети с одним входным вектором может быть задана с помощью R − обозначения S1 − S2 −... − SM, где задано количество элементов входного вектора и количество нейронов в каждом слое.
Та же трехслойная сеть также может быть нарисована с помощью сокращенного обозначения.
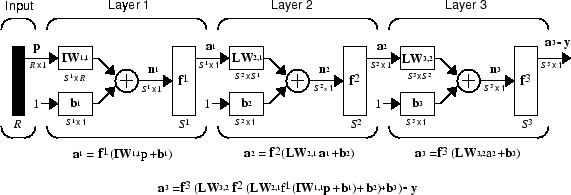
Многослойные сети довольно мощны. Например, сеть из двух слоев, где первый слой является сигмоидным, а второй слой линейным, может быть обучена произвольно хорошо аппроксимировать любую функцию (с конечным числом разрывов). Этот вид двухслойной сети широко используется в Многослойных Неглубоких Нейронных Сетях и Обучении Обратному Распространению.
Здесь принято, что выход третьего слоя, a3, является интересующим выходом сети, и этот вывод помечен как y. Это обозначение используется для задания выхода многослойных сетей.
Сетевые входы могут иметь связанные функции обработки. Функции обработки преобразуют входные данные пользователя в форму, которая легче или более эффективна для сети.
Для образца, mapminmax преобразует входные данные так, чтобы все значения попадали в интервал [− 1, 1]. Это может ускорить обучение для многих сетей .removeconstantrows удаляет строки вектора входа, которые соответствуют элементам входа которые всегда имеют одно и то же значение, потому что эти элементы входа не предоставляют сети никакой полезной информации. Третья функция общей обработки является fixunknowns, который перекодирует неизвестные данные (представленные в данных пользователя с NaN значения) в числовую форму для сети. fixunknowns сохраняет информацию о том, какие значения известны и какие неизвестны.
Точно так же выходы сети могут также иметь связанные функции обработки. Выходы обработки используются для преобразования предоставляемых пользователем целевых векторов для использования в сети. Затем выходы сети обрабатываются назад с помощью тех же функций, чтобы получить выходные данные с теми же характеристиками, что и исходные пользовательские целевые системы.
Оба mapminmax и removeconstantrows часто связаны с выходами сети. Однако, fixunknowns is not. Неизвестные значения в целях (представлено NaN значения) не должны изменяться для использования в сети.
Функции обработки описаны более подробно в Выборе функций обработки ввода-вывода нейронной сети.