Следующие разделы проведут вас через процесс вычисления задержек канала, необходимых для идеальной реконструкции вейвлета. Этот пример использует ex_wavelets модель, но можно применить процесс, чтобы выполнить идеальную реконструкцию вейвлета в любой модели. Чтобы открыть модель примера, введите ex_wavelets в MATLAB® командная строка.
Примечание
Для запуска Toolbox™ необходимо иметь лицензию продукта Wavelet ex_wavelets модель.
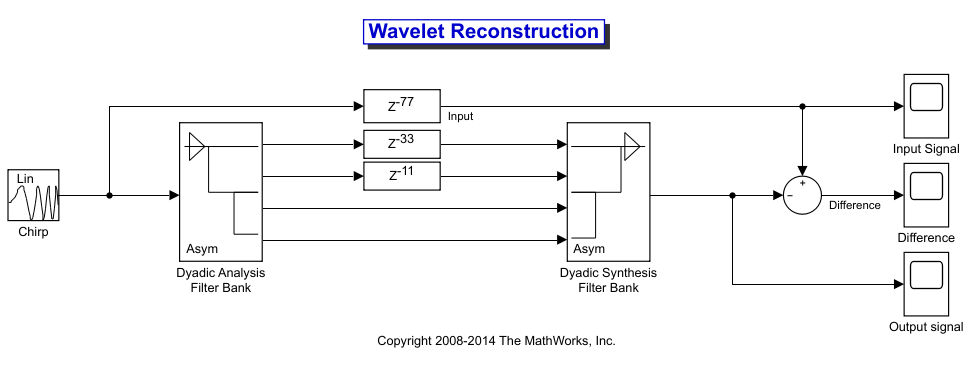
Прежде чем вы сможете начать вычислять задержки, необходимые для идеальной реконструкции вейвлета, вы должны знать типы фильтров, используемых в вашей модели.
Dyadic Analysis Filter Bank и Dyadic Synthesis Filter Bank блокируются в ex_wavelets модель имеет следующие настройки:
Filter = Biorthogonal
Filter order [synthesis/analysis] = [3/5]
Number of levels = 3
Tree structure = Asymmetric
Input = Multiple ports
На основе этих настроек Dyadic Analysis Filter Bank и Dyadic Synthesis Filter Bank блоков создать биортогональные фильтры с использованием Wavelet Toolbox wfilters функция.
Как только вы знаете типы фильтров, используемых блоками Dyadic Analysis и Dyadic Synthesis Filter Bank, вам нужно вычислить групповую задержку этих фильтров. Для этого можно использовать Signal Processing Toolbox™ fvtool.
Прежде чем вы сможете использовать fvtoolСначала необходимо восстановить фильтры в рабочем пространстве MATLAB. Для этого введите следующий код в командной строке MATLAB:
[Lo_D, Hi_D, Lo_R, Hi_R] = wfilters('bior3.5')
Где Lo_D и Hi_D представляют низко- и высокопроходные фильтры, используемые блоком Dyadic Analysis Filter Bank, и Lo_R и Hi_R представляют низко- и высокопроходные фильтры, используемые блоком Dyadic Synthesis Filter Bank.
После создания фильтров в рабочем пространстве MATLAB можно использовать fvtool для определения групповой задержки фильтров. Чтобы проанализировать биортогональный фильтр lowpass, используемый блоком Dyadic Analysis Filter Bank, вы должны сделать следующее:
Тип fvtool(Lo_D) в командной строке MATLAB для запуска Filter Visualization Tool.
Когда откроется Filter Visualization Tool, нажмите кнопку Group delay response ![]() () на панели инструментов или выберите Group Delay Response из Analysis меню.
() на панели инструментов или выберите Group Delay Response из Analysis меню.
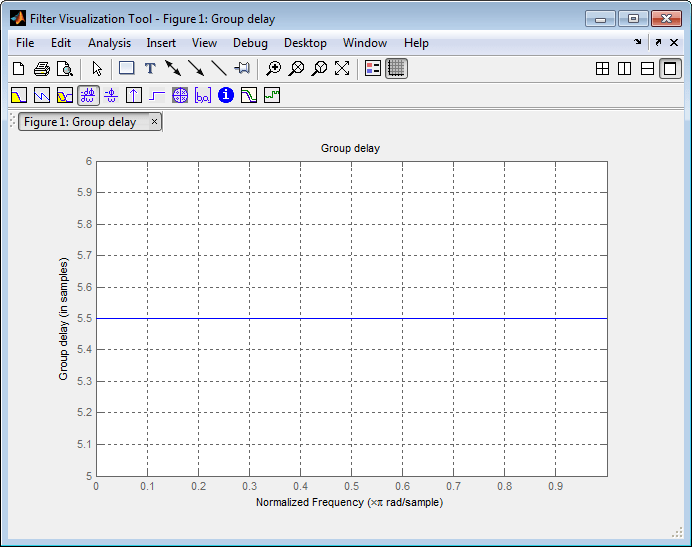
Основываясь на анализе Filter Visualization Tool, можно увидеть, что групповая задержка низкочастотного биортогонального фильтра Dyadic Analysis Filter Bank составляет 5,5.
Примечание
Повторите эту процедуру, чтобы проанализировать групповую задержку каждого из фильтров в вашей модели. В этом разделе не показаны результаты для каждого фильтра в ex_wavelets модель, потому что все вейвлет в этом конкретном примере имеют одинаковую групповую задержку.
Чтобы определить задержку, введенную системой банка фильтров анализа и синтеза, необходимо восстановить древовидные структуры блоков Dyadic Analysis Filter Bank и Dyadic Synthesis Filter Bank. Чтобы узнать больше о построении древовидных структур для блоков Dyadic Analysis Filter Bank и Dyadic Synthesis Filter Bank, смотрите следующие разделы DSP System Toolbox™ Руководство:
Потому что фильтр блокируется в ex_wavelets модель использует биортогональные фильтры с тремя уровнями и асимметричной древовидной структурой, система банка фильтров появляется как показано на следующем рисунке.
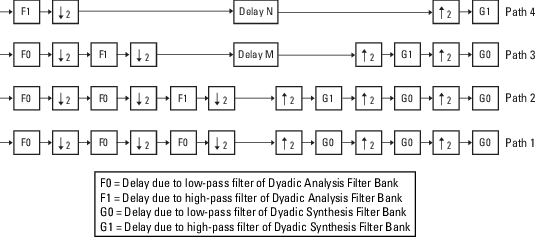
Дополнительные значения задержки M и N на путях 3 и 4 на предыдущем рисунке гарантируют, что общая задержка на каждом из четырех путей фильтра идентична.
Теперь, когда вы восстановили систему банка фильтров, можно вычислить задержку на каждом пути фильтра. Для этого используйте следующие благородные тождества:
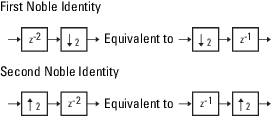
Можно применить Noble тождеств, суммируя задержку на каждом сигнальном пути справа налево. Первый Noble тождеств указывает, что перемещение задержки 1 перед понижением 2 эквивалентно умножению этого значения задержки на 2. Точно так же вторые тождества Noble указывают, что перемещение задержки 2 перед повышением частоты 2 эквивалентно делению этого значения задержки на 2.
The fvtool анализ на шаге 1 показал, что как низко-, так и высокопроходные фильтры группы фильтров анализа имеют одну и ту же групповую задержку (F0 = F1 = 5,5). Таким образом, можно использовать F, чтобы представлять групповую задержку банка фильтров анализа. Точно так же групповая задержка низко- и высокопроходных фильтров группы синтезирующих фильтров одинаковая (G0 = G1 = 5,5), поэтому можно использовать G, чтобы представлять групповую задержку группы синтезирующих фильтров.
Следующий рисунок показывает систему банка фильтров с промежуточными суммами задержек, отображаемыми ниже каждого пути.
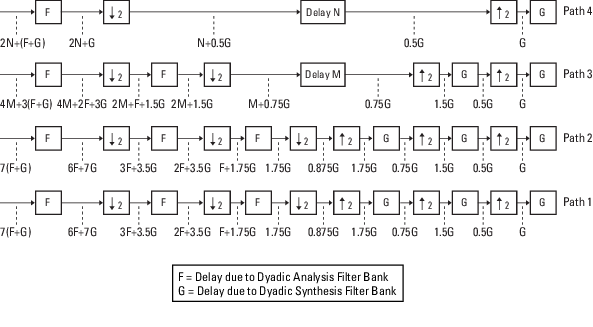
На предыдущем рисунке видно, что задержки сигнала на путях 1 и 2 идентичны: 7 (F + G). Поскольку каждый путь системы банка фильтров имеет идентичную задержку, можно приравнять уравнения задержки для путей 3 и 4 к уравнению задержки для путей 1 и 2. После построения этих уравнений можно решить для M и N, соответственно:
The fvtool анализ на этапе 1 показал, что групповая задержка каждого биортогонального вейвлет в этой модели составляет 5,5 выборки. Поэтому F = 5,5 и G = 5,5. Вставив эти значения в два предыдущих уравнения, вы получаете M = 11 и N = 33. Поскольку общая задержка на каждом пути фильтра должна быть одинаковой, можно найти общую задержку системы банка фильтров, вставив F = 5,5 и G = 5,5 в уравнение задержки для любого из четырех путей фильтра. Вставка значений F и G в 7 (F + G) приводит к общей задержке 77 отсчетов для системы банка фильтров ex_wavelets модель.
Теперь, когда вы знаете задержки, необходимые для идеальной реконструкции вейвлета, можно включить эти значения задержки в модель. The ex_wavelets модель уже была обновлена с правильными значениями задержки (M = 11, N = 33, Overall = 77), поэтому готова к запуску.
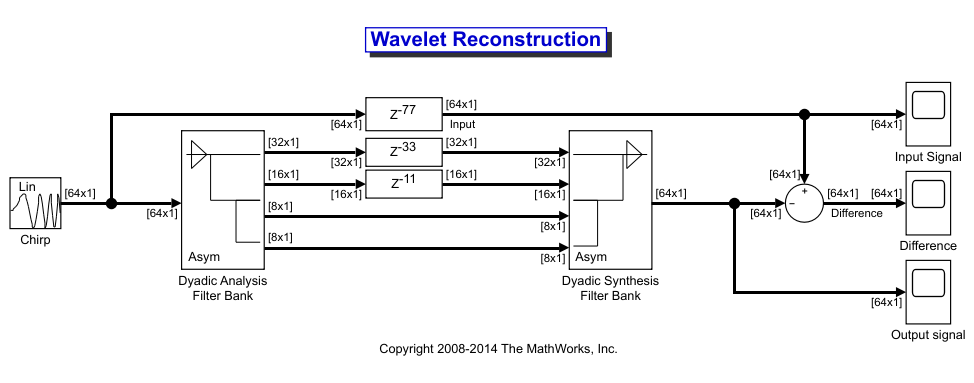
После запуска модели исследуйте ошибку восстановления в возможностях « Различии». Чтобы дополнительно изучить любые интересующие области, используйте инструменты масштабирования, доступные на панели инструментов окна возможностей или из View меню.
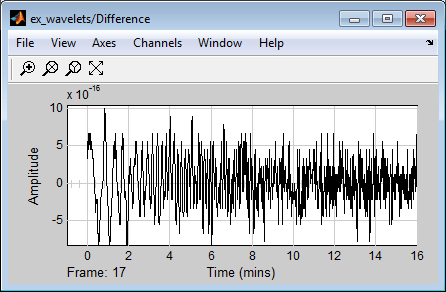
[1] Strang, G. and Nguyen, T. Wavelets and Filter Banks. Wellesley, MA: Wellesley-Cambridge Press, 1996.