В цифровом оборудовании номера сохраняются в двоичных словах. Двоичное слово является последовательностью бит с фиксированной длиной (1 и 0). Способ интерпретации аппаратными компонентами или программными функциями этой последовательности 1 и 0 определяется типом данных.
Двоичные числа представлены как типы данных с плавающей точкой или с фиксированной точкой. В этом разделе мы обсуждаем многие термины и концепции, касающиеся чисел с фиксированной точкой, типов данных и математики.
Тип данных с фиксированной точкой характеризуется размером слова в битах, положением двоичной точки и сигнальностью числа, которое может быть подписано или не подписано. Подписанные числа и типы данных могут представлять как положительные, так и отрицательные значения, в то время как неподписанные числа и типы данных могут представлять только значения, которые больше или равны нулю.
Положение двоичной точки является средством, с помощью которого значения с фиксированной точкой масштабируются и интерпретируются.
Например, двоичное представление обобщенного числа с фиксированной точкой (со знаком или без знака) показано ниже:
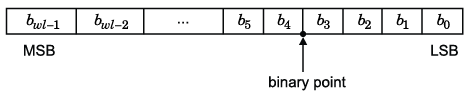
где
bi является ith двоичная цифра.
wl - количество бит в двоичном слове, также известное как размер слова.
b wl -1 является местоположением самого значимого, или самого высокого, бита (MSB). В двоичных числах со знаком этот бит является битом знака, который указывает, положительное или отрицательное число.
b0 - местоположение наименее значимого, или самого низкого, бита (LSB). Этот бит в двоичном слове может представлять наименьшее значение. Вес LSB определяется:
где, fractionlength - количество бит справа от двоичной точки.
Биты слева от двоичной точки являются целочисленными битами и/или битами со знаком, а биты справа от двоичной точки являются дробными битами. Количество бит слева от двоичной точки известно как целочисленная длина. Двоичная точка в этом примере показана на четырех местах слева от LSB. Поэтому число, как говорят, имеет четыре дробных бита или длину дроби четыре.
Типы данных с фиксированной точкой могут быть либо подписанными, либо неподписанными.
Подписанные двоичные номера с фиксированной точкой обычно представлены одним из трех способов:
Знак/амплитуда - Представление подписанной фиксированной точки или чисел с плавающей запятой. В представлении знака/амплитуды один бит двоичного слова всегда является выделенным знаком, в то время как остальные биты слова кодируют величину числа. Отрицание с использованием представления знак/амплитуда состоит из переворачивания бита знака с 0 (положительный) на 1 (отрицательный) или с 1 до 0.
Свое дополнение
Дополнение двух - дополнение двух является наиболее распространенным представлением подписанных чисел с фиксированной точкой. Для получения дополнительной информации см. раздел «Дополнение двух».
Неподписанные числа с фиксированной точкой могут представлять только числа, большие или равные нулю.
В представлении [Смещение наклона] номера с фиксированной точкой могут быть закодированы согласно схеме
где наклон может быть выражен как
Термин корректировка наклона иногда используется в качестве синонима дробного наклона.
В тривиальном случае наклон = 1 и смещение = 0. Масштабирование всегда тривиально для чистых целых чисел, таких как int8, а также для истинных типов с плавающей точкой single и double.
Целое число иногда называется сохраненным целым числом. Это необработанное двоичное число, в котором двоичная точка принята в крайнем правом углу слова. В System Toolboxes отрицательное значение степени часто упоминается как длина дроби.
Наклон и смещение вместе представляют масштабирование числа с фиксированной точкой. В числе с нулевым смещением только наклон влияет на масштабирование. Число с фиксированной точкой, которое масштабируется только двоичным положением точки, эквивалентно числу в представлении Fixed-Point Designer™ [Смещение Откоса], которое имеет смещение, равное нулю и регулировку наклона, равную единице. Это упоминается как двоичное масштабирование только для точек или масштабирование степени двойки:
или
В программном обеспечении System Toolbox можно задать тип данных с фиксированной точкой и масштабирование для выхода или параметров многих блоков путем определения размера слова и длины дроби величины. Длина размера слова и фракции задают весь тип данных и информацию о масштабировании для сигналов только с двоичной точкой.
Все блоки System Toolbox, поддерживающие типы данных с фиксированной точкой, поддерживают сигналы с масштабированием только с двоичной точкой. Многие блоки с фиксированной точкой, которые не выполняют арифметические операции, но просто переставляют данные, такие как Delay и Matrix Transpose, также поддерживают сигналы с масштабированием [Slope Bias].
Вы должны обратить внимание на точность и область значений типов данных с фиксированной точкой и масштабированиями, которые вы выбираете для блоков в ваших симуляциях, в порядок знать, будут ли вызываться методы округления или будут ли происходить переполнения.
Область значений является диапазоном чисел, которые могут представлять тип данных с фиксированной точкой и масштабирование. Ниже проиллюстрирована область значений представимых чисел для дополнительного числа с фиксированной точкой размера слова wl, масштабирования S и B смещения:

Для как подписанных, так и неподписанных номеров с фиксированной точкой любого типа данных количество различных битовых шаблонов составляет 2wl.
Например, в дополнении двух отрицательные числа должны быть представлены, а также нули, поэтому максимальное значение равно 2wl–1. Поскольку существует только одно представление для нуля, существует неравное число положительных и отрицательных чисел. Это означает, что существует представление для -2wl–1 но не для 2wl–1:
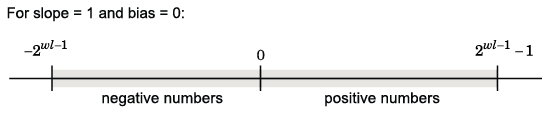
Полная область значений является самой широкой областью значений для типа данных. Для типов с плавающей запятой полный спектр - ∞ к ∞. Для целых типов полная область значений является областью значений от наименьшего до наибольшего целочисленного значения (конечного), которое может представлять тип. Для примера от -128 до 127 для знакового 8-битного целого числа.
Обработка переполнения. Поскольку тип данных с фиксированной точкой представляет числа в конечной области значений, переполнение может произойти, если результат операции больше или меньше, чем числа в этой области значений.
Программное обеспечение Тулбокса системы не позволяет вам добавлять защитные биты к типу данных на лету в порядок, чтобы избежать переполнения. Защитные биты являются дополнительными битами в регистре оборудования или симуляции программного обеспечения, которые добавляются в верхний конец двоичного слова, чтобы гарантировать, что никакая информация не будет потеряна в случае переполнения. Любые защитные биты должны быть выделены после инициализации модели. Однако программное обеспечение позволяет вам либо насыщать, либо обернуть переполнения. Насыщение представляет положительное переполнение как самое большое положительное число в используемой области значений и отрицательное переполнение как самое большое отрицательное число в используемой области значений. Wrapping использует арифметику по модулю, чтобы привести переполнение назад в представимую область значений типа данных. Для получения дополнительной информации см. арифметику по модулю».
Точность числа с фиксированной точкой является различием между последовательными значениями, представимыми его типом данных, и масштабированием, которое равно значению его наименее значимого бита. Значение наименее значимого бита, и, следовательно, точность числа, определяется количеством дробных бит. Значение с фиксированной точкой может быть представлено в пределах половины точности его типа данных и масштабирования. Термин разрешение иногда используется в качестве синонима этого определения.
Для примера представление с фиксированной точкой с четырьмя битами справа от двоичной точки имеет точность 2-4 или 0,0625, которое является значением его наименее значимого бита. Любое число в области значений этого типа данных и масштабирования может быть представлено в пределах (2-4)/2 или 0,03125, что вдвое меньше точности. Это пример представления числа с конечной точностью.
Режимы округления. Когда вы представляете числа с конечной точностью, не каждое число в доступной области значений может быть точно представлено. Если число не может быть точно представлено заданным типом данных и масштабированием, оно округлится до представимого числа. Хотя точность всегда теряется в операции округления, стоимость операции и количество введенного смещения зависят от самого режима округления. Чтобы предоставить вам большую гибкость в компромиссе между стоимостью и смещением, программное обеспечение DSP System Toolbox™ в настоящее время поддерживает следующие режимы округления:
Ceiling округляет результат вычисления до ближайшего представимого числа в направлении положительной бесконечности.
Convergent округляет результат вычисления до ближайшего представимого числа. В случае галстука Convergent округляет до ближайшего четного числа. Это наименее смещенный режим округления, обеспечиваемый тулбоксом.
Floor, что эквивалентно усечению, округляет результат вычисления до ближайшего представимого числа в направлении отрицательной бесконечности. Операция усечения приводит к отбрасыванию одного или нескольких наименее значимых битов из числа.
Nearest округляет результат вычисления до ближайшего представимого числа. В случае галстука Nearest округляет до ближайшего представимого числа в направлении положительной бесконечности.
Round округляет результат вычисления до ближайшего представимого числа. В случае галстука Round округляет положительные числа до ближайшего представимого числа в направлении положительной бесконечности и округляет отрицательные числа до ближайшего представляемого числа в направлении отрицательной бесконечности.
Simplest округляет результат вычисления с использованием режима округления (Floor или Zero), который добавляет наименьшее количество дополнительного округляющего кода к вашему сгенерированному коду. Для получения дополнительной информации смотрите Режим округления: самый простой (Fixed-Point Designer).
Zero округляет результат вычисления до ближайшего представимого числа в направлении нуля.
Дополнительные сведения о каждом из этих режимов округления см. в разделе Округление (Fixed-Point Designer).
Для прямого сравнения режимов округления смотрите Выбор метода округления (Fixed-Point Designer).