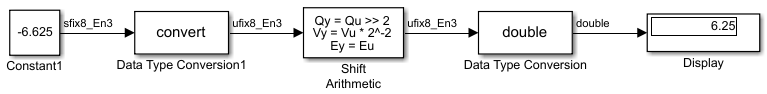Правила для арифметических операций

Арифметика с фиксированной точкой относится к тому, как управляются подписанные или неподписанные двоичные слова. Простота арифметических функций с фиксированной точкой, таких как сложение и вычитание, позволяет проводить экономически эффективные аппаратные реализации.

В следующих разделах описываются правила, которые Simulink^® программное обеспечение выполняется при выполнении арифметических операций на входах и параметрах. Эти правила организованы в четыре группы на основе соответствующих операций: сложение и вычитание, умножение, деление и сдвиги. Для каждой из этих четырех групп правила выполнения указанной операции представлены в примере с использованием правил.

Вычислительные модули

Архитектура ядра многих процессоров содержит несколько вычислительные модули арифметики включая модули логики (ALU), умножение и накопление модулей (MAC) и переключатели. Эти вычислительные модули обрабатывают двоичные данные непосредственно и обеспечивают поддержку арифметических расчетов различной точности. ALU выполняет стандартный набор арифметических и логических операций, а также деление. MAC выполняет операции умножения, умножения/сложения и умножения/вычитания. Переключатель выполняет логические и арифметические сдвиги, нормализацию, денормализацию и другие операции.

Сложение и вычитание

Сложение является наиболее распространенной арифметической операцией, которую выполняет процессор. Когда два n-битовых числа складываются вместе, всегда можно получить результат с n + 1 ненулевыми цифрами из-за переноса из самой левой цифры. Для сложения двух дополнительных чисел существует три случая:

Если оба числа положительны, и результат их сложения имеет бит знака 1, то произошло переполнение; в противном случае результат будет правильным.
Если оба числа отрицательны, и знак результата 0, то произошло переполнение; в противном случае результат будет правильным.
Если числа отличаются от знака, переполнение не может произойти, и результат всегда верен.

Процесс суммирования блоков Simulink с фиксированной точкой

Рассмотрим суммирование двух чисел. В идеале вещественные значения подчиняются уравнению

$V_{a} = \pm V_{b} \pm V_{c},$

где _Vb и _Vc являются входом значениями, а _Va является выходом значением. Чтобы увидеть, как суммирование фактически реализовано, три идеальных значения должны быть заменены общей схемой кодирования [Slope Bias], описанной в масштабировании:

$V_{i} = F_{i} 2^{E_{i}} Q_{i} + B_{i} .$

Уравнение в Сложении даёт решение получившегося уравнения для сохраненного целого числа, _Qa. Используя краткое обозначение, это уравнение становится

$Q_{a} = \pm F_{s b} 2^{E_{b} - E_{a}} Q_{b} \pm F_{s c} 2^{E_{c} - E_{a}} Q_{c} + B_{n e t},$

где _Fsb и _Fsc - скорректированные дробные склоны, а _Bnet - смещение сети. Оффлайн-преобразования и онлайн-преобразования и операции обсуждаются ниже.

Автономные преобразования. _Fsb, _Fsc и _Bnet вычисляются в автономном режиме с использованием округления к ближайшему и насыщения. Кроме того, _Bnet хранится с использованием типа выходных данных.

Онлайн-конверсии и операции. Остальные операции выполняются в оперативном режиме процессором с фиксированной точкой и зависят от наклонов и смещений для типов входных и выходных данных. Худший (самый неэффективный) случай происходит, когда склоны и смещения несоответствуют. Преобразования и операции в наихудшем случае описываются следующими шагами:

Начальное значение для _Qa определяется смещением сети, _Bnet:
$Q_{a} = B_{n e t} .$
Первое входное целое значение, _Qb, умножается на скорректированный наклон, _Fsb:
$Q_{R a w P r o d u c t} = F_{s b} Q_{b} .$
Предыдущий продукт преобразуется в измененный тип выходных данных, где наклон равен единице, а смещение равняется нулю:
$Q_{T e m p} = c o n v e r t (Q_{R a w P r o d u c t}) .$
Это преобразование включает любую необходимую перемену битов, округление или обработку переполнения.
Операция суммирования выполняется:
$Q_{a} = Q_{a} \pm Q_{T e m p} .$
Это суммирование включает любую необходимую обработку переполнения.
Шаги 2-4 повторяются для каждого числа, которое должно быть суммировано.

Важно отметить, что перемена битов, округление и обработка переполнения применяются к промежуточным этапам (3 и 4), а не к общей сумме.

Для получения дополнительной информации смотрите Процесс суммирования.

Оптимизация симуляций и сгенерированного кода

Если масштабирование входного и выходного сигналов совпадает, количество операций суммирования уменьшается с худшего (наиболее неэффективного) случая. Для примера, когда вход имеет тот же дробный наклон, что и выход, шаг 2 уменьшается до умножения на единицу и может быть устранен. Тривиальные шаги в процессе суммирования устраняются как для симуляции, так и для генерации кода. Исключительное использование двоичного масштабирования только для точек как для входных сигналов, так и для выходных сигналов является общим способом устранения несоответствий склонов и смещений, и приводит к наиболее эффективным симуляциям и сгенерированному коду.

Умножение

Умножение n-битового двоичного числа с m-битным двоичным числом приводит к продукту, которая до m + n бит в длину для слов с знаком и без знака. Большинство процессоров выполняют умножение n-бит на n-бит и получают 2n-бит результата (двойные биты), принимая, что нет условия переполнения.

Процесс умножения блоков Simulink с фиксированной точкой

Рассмотрим умножение двух чисел. В идеале вещественные значения подчиняются уравнению

$V_{a} = V_{b} V_{c} .$

где _Vb и _Vc являются входом значениями, а _Va является выходом значением. Чтобы увидеть, как умножение фактически реализовано, три идеальных значения должны быть заменены общей схемой кодирования [Slope Bias], описанной в масштабировании:

$V_{i} = F_{i} 2^{E_{i}} Q_{i} + B_{i} .$

Решение получившегося уравнения для выхода сохраненного целого числа, _Qa, приведено ниже:

$\begin{matrix} Q_{a} = \frac{F_{b} F_{c}}{F_{a}} 2^{E_{b} + E_{c} - E_{a}} Q_{b} Q_{c} + \frac{F_{b} B_{c}}{F_{a}} 2^{E_{b} - E_{a}} Q_{b} \\ + \frac{F_{c} B_{b}}{F_{a}} 2^{E_{c} - E_{a}} Q_{c} + \frac{B_{b} B_{c} - B_{a}}{F_{a}} 2^{- E_{a}} . \end{matrix}$

Умножение с ненулевыми смещениями и несоответствующими дробными склонами. Реализация вышеописанного уравнения в худшем случае происходит, когда наклоны и смещения входного и выходного сигналов несоответствуют. В таких случаях для выполнения высокоуровневого умножения (или деления) требуется несколько низкоуровневых целочисленных операций. Выбор реализации этих низкоуровневых расчетов может повлиять на вычислительную эффективность, ошибки округления и переполнение.

В блоках Simulink фактическое умножение или операция деления всегда выполняется для переменных с фиксированной точкой, которые имеют нулевые смещения. Если вход имеет ненулевое смещение, он преобразуется в представление, которое имеет масштабирование только для двоичных точек перед операцией. Если результатом является ненулевое смещение, операция сначала выполняется с временными переменными, которые имеют двоичное масштабирование только для точек. Результат затем преобразуется в тип данных и масштабирование конечного выхода.

Если и входы, и выход имеют ненулевые смещения, то операция разбивается следующим образом:

$\begin{array}{l} V_{1 T e m p} = V_{1}, \\ V_{2 T e m p} = V_{2}, \\ V_{3 T e m p} = V_{1 T e m p} V_{2 T e m p}, \\ V_{3} = V_{3 T e m p}, \end{array}$

где

$\begin{array}{l} V_{1 T e m p} = 2^{E_{1 T e m p}} Q_{1 T e m p}, \\ V_{2 T e m p} = 2^{E_{2 T e m p}} Q_{2 T e m p}, \\ V_{3 T e m p} = 2^{E_{3 T e m p}} Q_{3 T e m p} . \end{array}$

Эти уравнения показывают, что временные переменные имеют двоичное масштабирование только для точек. Однако уравнения не указывают сигнальность, размеры слова или значения фиксированной экспоненты этих переменных. Программа Simulink присваивает эти свойства временным переменным на основе следующих целей:

Представление исходного значения без переполнения.
Тип данных и масштабирование исходного значения определяют максимальное и минимальное значение реального мира:

$V_{M a x} = F 2^{E} Q_{M a x I n t e g e r} + B,$

$V_{M i n} = F 2^{E} Q_{M i n I n t e g e r} + B .$
Тип данных и масштабирование временного значения должны быть в состоянии представлять эту область значений без переполнения. Потеря точности возможна, но переполнение никогда не допускается.
Используйте тип данных, который приводит к эффективным операциям.
Эта цель относится к цели, которую вы будете использовать для производственного развертывания вашего проекта. Например, предположим, что вы реализуете проект на 16-битном процессоре с фиксированной точкой, который обеспечивает 32-битную long, 16-битный intи 8-битные short или char. Для такой цели сохранение эффективности означает, что используется не более 32 биты, и меньшие размеры 8 или 16 бит используются, если они достаточны для поддержания точности.
Обеспечьте точность.
В идеале каждое возможное значение, заданное исходным типом данных и масштабированием, идеально представлено временной переменной. Однако это может потребовать больше биты, чем эффективно. Биты отбрасываются, что приводит к потере точности, в той степени, в которой это необходимо для сохранения эффективности.

Например, рассмотрим следующее, принимая 16-битную цель микропроцессора:

$V_{O r i g i n a l} = Q_{O r i g i n a l} + - 43.25,$

где _QOriginal - 8-битный беззнаковый тип данных. Для этого типа данных,

$\begin{matrix} Q_{M a x I n t e g e r} = 225, \\ Q_{M i n I n t e g e r} = 0, \end{matrix}$

так

$\begin{matrix} V_{M a x} = 211.75, \\ V_{M i n} = - 43.25. \end{matrix}$

Минимальное возможное значение отрицательное, поэтому временная переменная должна быть подписанным целочисленным типом данных. Исходная переменная имеет наклон 1, но смещение выражается с большей точностью двумя цифрами после двоичной точки. Чтобы получить полную точность, фиксированная экспонента временной переменной должна быть -2 или менее. Программное обеспечение Simulink выбирает наименее возможную точность, которая обычно является наиболее эффективной, если только не возникают проблемы переполнения. Для масштабирования 2^-2выбор 16-разрядной или 32-разрядной подписи позволяет избежать переполнения. Для эффективности программное обеспечение Simulink выбирает меньший выбор из 16 бит. Если исходная переменная является входом, то уравнения для преобразования во временную переменную

$\begin{array}{l} \begin{matrix} uint8_T & Q_{O r i g i n a l}, \\ uint16_T & Q_{T e m p}, \end{matrix} \\ Q_{T e m p} = ((uint16_T) Q_{O r i g i n a l} ≪ 2) - 173. \end{array}$

Умножение с нулевыми смещениями и несоответствующими дробными склонами. Когда смещения равны нулю, и дробные склоны несоответствуют, реализация уменьшается до

$Q_{a} = \frac{F_{b} F_{c}}{F_{a}} 2^{E_{b} + E_{c} - E_{a}} Q_{b} Q_{c} .$

Автономные преобразования

Количество

$F_{N e t} = \frac{F_{b} F_{c}}{F_{a}}$

Вычисляется в автономном режиме с использованием округления к ближайшему и насыщения. _FNet хранится с использованием типа данных с фиксированной точкой формы

$2^{E_{N e t}} Q_{N e t},$

где _ENet и _QNet выбираются автоматически, чтобы наилучшим образом представлять _FNet.

Онлайн-преобразования и операции

Целочисленные значения _Qb и _Qc умножаются:
$Q_{R a w P r o d u c t} = Q_{b} Q_{c} .$
Чтобы сохранить полную точность продукта, двоичная точка _QRawProduct задается суммой двоичных точек _Qb и _Qc.
Предыдущий продукт преобразуется в тип выходных данных:
$Q_{T e m p} = c o n v e r t (Q_{R a w P r o d u c t}) .$
Это преобразование включает любую необходимую перемену битов, округление или обработку переполнения. Преобразования сигналов обсуждают преобразования.
Умножение
$Q_{2 R a w P r o d u c t} = Q_{T e m p} Q_{N e t}$
выполняется.
Предыдущий продукт преобразуется в тип выходных данных:
$Q_{a} = c o n v e r t (Q_{2 R a w P r o d u c t}) .$
Это преобразование включает любую необходимую перемену битов, округление или обработку переполнения. Преобразования сигналов обсуждают преобразования.
Шаги с 1 по 4 повторяются для каждого дополнительного числа, которое должно быть умножено.

Умножение с нулевыми смещениями и совпадение дробных наклонов. Когда смещения равны нулю, а дробные склоны совпадают, реализация уменьшается до

$Q_{a} = 2^{E_{b} + E_{c} - E_{a}} Q_{b} Q_{c} .$

Автономные преобразования

Преобразования в автономном режиме не выполняются.

Онлайн-преобразования и операции

Целочисленные значения _Qb и _Qc умножаются:
$Q_{R a w P r o d u c t} = Q_{b} Q_{c} .$
Чтобы сохранить полную точность продукта, двоичная точка _QRawProduct задается суммой двоичных точек _Qb и _Qc.
Предыдущий продукт преобразуется в тип выходных данных:
$Q_{a} = c o n v e r t (Q_{R a w P r o d u c t}) .$
Это преобразование включает любую необходимую перемену битов, округление или обработку переполнения. Преобразования сигналов обсуждают преобразования.
Шаги 1 и 2 повторяются для каждого дополнительного числа, которое должно быть умножено.

Для получения дополнительной информации смотрите Процесс умножения.

Деление

В этом разделе рассматривается деление величин с нулевым смещением.

Примечание

Когда любой вход для вычисления деления имеет ненулевое смещение, выполненные операции точно совпадают с операциями для умножения, описанными в Умножении с ненулевыми смещениями и несоответствующими дробными склонами.

Процесс деления блоков Simulink с фиксированной точкой

Рассмотрим деление двух чисел. В идеале вещественные значения подчиняются уравнению

$V_{a} = V_{b} / V_{c},$

где _Vb и _Vc являются входом значениями, а _Va является выходом значением. Чтобы увидеть, как действительно реализовано деление, три идеальных значения должны быть заменены общей схемой кодирования [Slope Bias], описанной в масштабировании:

$V_{i} = F_{i} 2^{E_{i}} Q_{i} + B_{i} .$

Для случая, когда коэффициенты регулировки наклона едины, а смещения равны нулю для всех сигналов, решение получившегося уравнения для выхода сохраненного целого числа Qa задается следующим уравнением:

$Q_{a} = 2^{E_{b} - E_{c} - E_{a}} (Q_{b} / Q_{c}) .$

Это уравнение включает целочисленное деление и некоторые битовые сдвиги. Если _Ea > _Eb - Ec, то любые битовые сдвиги направо и реализация проста. Однако, если Ea < Eb - Ec, то битовые сдвиги идут налево, и реализация может оказаться более сложной. Существенной проблемой является то, что выход имеет большую точность, чем обеспечивает целое деление. Чтобы получить полную точность, необходимо дробное деление. Язык программирования C предоставляет доступ к целому делению только для типов данных с фиксированной точкой. В зависимости от размера числителя, можно получить некоторые дробные биты, выполнив сдвиг перед целым делением. В худшем случае может оказаться необходимым прибегнуть к многократному вычитанию в программном обеспечении.

В целом, деление значений является операцией, которую следует избегать во встраиваемых системах с фиксированной точкой. Деление, где выход имеет большую точность, чем целое деление (то есть _Ea < _Eb - Ec), должно использоваться с еще большей реактивностью.

Для получения дополнительной информации см. раздел «Процесс деления».

Сдвиги

Почти все микропроцессоры и цифровые сигнальные процессоры поддерживают четко определенные операции битового сдвига (или просто сдвига) для целых чисел. Для примера рассмотрим 8-битное беззнаковое целое число 00110101. Результаты сдвига на 2 бита влево и сдвига на 2 бита вправо показаны в следующей таблице.

Операция сдвига	Двоичное значение	Десятичное значение
Нет сдвига (исходный номер)	00110101	53
Сдвиньте влево на 2 бита	11010100	212
Сдвиньте вправо на 2 бита	00001101	13

Сдвиг можно выполнить с помощью блока Shift Arithmetic Simulink. Используйте этот блок для выполнения битового сдвига, двоичного сдвига точки или обоих

Сдвигающие биты вправо

Особый случай сдвига бит вправо требует фактора обработки крайнего левого бита, который может содержать информацию о знаке. Сдвиг вправо может быть классифицирован как логический сдвиг вправо или арифметический сдвиг вправо. Для логического сдвига вправо 0 включено в самый значащий бит для каждого битового сдвига. Для арифметического сдвига вправо самый значительный бит рециркулируется для каждого битового сдвига.

Блок Shift Arithmetic выполняет арифметический сдвиг вправо и, следовательно, рециркулирует самый значительный бит для каждого сдвига бита вправо. Например, учитывая фиксированную точку номер 11001.011 (-6.625), немного сдвига два места направо с запятой в двоичном числе неперемещенные выражения номер 11110.010 (-1.75), как показано в модели ниже:

Чтобы выполнить логический сдвиг прямо по номеру со знаком с помощью арифметики, используйте блок Data Type Conversion, чтобы привести число как беззнаковое число эквивалентной длины и масштабирования. Эта модель показывает, что номер со знаком с фиксированной точкой 11001.001 (-6.625) становится 00110.010 (6.25).

Документация