patternsearch и Optimize Задача Live EditorВ этом примере показано, как решить ограниченную задачу минимизации, используя как задачу Optimize Live Editor, которая предлагает визуальный подход, так и командную строку.
Задача включает использование линейных и нелинейных ограничений при минимизации нелинейной функции с patternsearch. Целевая функция является
где
H = [36 17 19 12 8 15;
17 33 18 11 7 14;
19 18 43 13 8 16;
12 11 13 18 6 11;
8 7 8 6 9 8;
15 14 16 11 8 29];
f = [ 20 15 21 18 29 24 ]';
F = @(x)0.5*x'*H*x + f'*x;
Эта целевая функция также включена в ваше программное обеспечение в файл lincontest7.m.
Линейные ограничения
где
A = [-8 7 3 -4 9 0];
b = 7;
Aeq = [7 1 8 3 3 3;
5 0 -5 1 -5 8;
-2 -6 7 1 1 9;
1 -1 2 -2 3 -3];
beq = [84 62 65 1]';Введите предыдущие секции кода, чтобы получить переменные задачи в рабочую область перед продолжением.
patternsearch в задаче оптимизации Live EditorСоздайте новый live скрипт, нажав кнопку New Live Script в разделе File на вкладке Home.
Вставьте задачу Optimize Live Editor. Щелкните вкладку Insert, а затем в разделе Code выберите Task > Optimize.
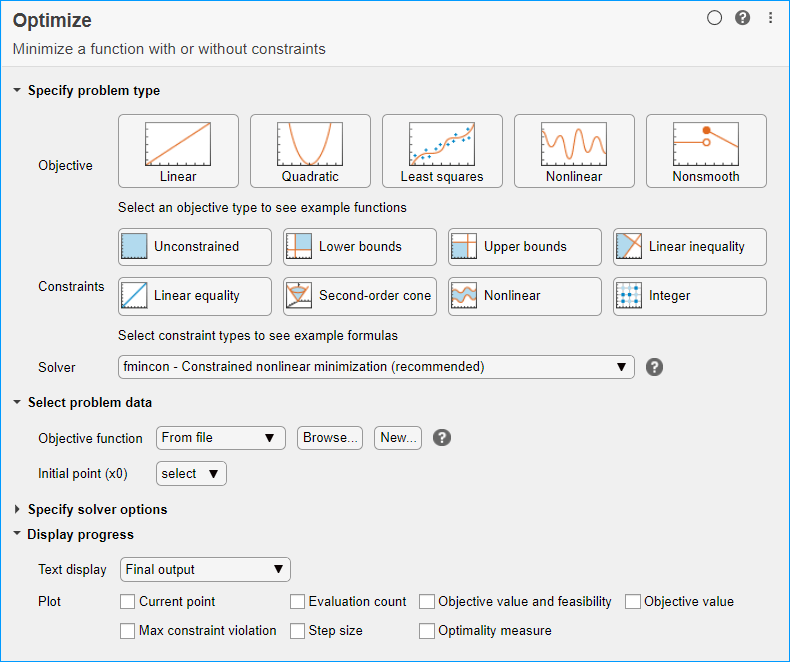
Задайте тип задачи
В Specify problem type разделе задачи нажмите кнопку Objective > Nonlinear.
Нажмите кнопки Constraints > Linear inequality и Linear equality.
Выберите Solver > patternsearch - Pattern search.
Выберите данные задачи
Введите переменные задачи в Select problem data разделе задачи. Чтобы задать целевую функцию, выберите Objective function > Function handle и выберите F.
Установите ограничения неравенства равными A и b. Установите ограничения равенства равными Aeq и beq.
Чтобы задать начальную точку, сначала необходимо создать новый раздел над задачей. Для этого нажмите кнопку Section Break на вкладке Insert. В новом разделе над задачей введите следующий код для начальной точки.
x0 = [2 1 0 9 1 0]';
Запустите раздел для размещения x0 в рабочую область. Чтобы запустить раздел, поместите курсор в раздел и нажмите клавишу Ctrl+Enter или щелкните синюю полосу слева от номера линии.
В Select problem data разделе задачи задайте x0 в качестве начальной точки.
Задайте опции решателя
Поскольку эта задача линейно ограничена, задайте дополнительную опцию решателя. Разверните раздел Specify solver options задачи и нажмите кнопку Add. Установите Poll settings > Poll method равным GSSPositiveBasis2N. Для получения дополнительной информации об эффективности методов опроса GSS для линейно ограниченных задач, смотрите Сравнение эффективности опций опроса.
Задание параметров отображения
В Display progress разделе задачи выберите Best value и Mesh size функции построения графика.
Ваша настройка выглядит следующим образом:
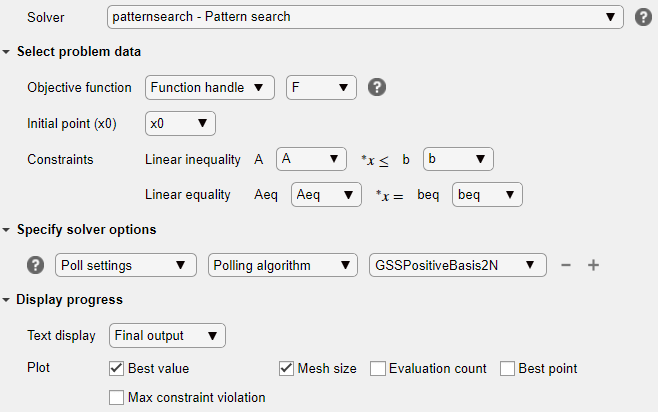
Запустите решатель и исследуйте результаты
Чтобы запустить решатель, нажмите кнопку options ⁝ в верхней части окна задачи и выберите Run Section.
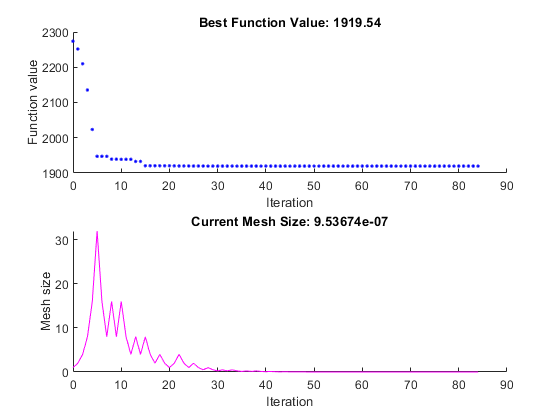
Графики появляются в отдельном окне рисунка и в области выхода задачи.
Чтобы получить точку решения и значение целевой функции в решении, посмотрите на верхнюю часть задачи.

The Optimize Задача Live Editor возвращает решение в переменной с именем solution и возвращает значение целевой функции в переменной с именем objectiveValue. Просмотрите эти значения путем ввода следующего кода в разделе под задачей и последующего запуска раздела или путем ввода кода в MATLAB® командная строка.
disp(solution)
8.5165
-6.1094
4.0989
1.2877
-4.2348
2.1812disp(objectiveValue)
1.9195e+03
Включите нелинейные ограничения
Добавьте к задаче следующие нелинейные ограничения.
Чтобы включить эти ограничения, сначала нажмите кнопку Constraints > Nonlinear.

В разделе Select problem data под Constraints выберите Nonlinear > Local function и нажмите кнопку New. Функция появится в новом разделе под задачей. Отредактируйте полученный код так, чтобы он содержал следующие линии.
function [c, ceq] = double_ineq(x) c = [-1.5 + x(1)*x(2) + x(1) - x(2); -x(1)*x(2) - 10]; ceq = []; end
В разделе Nonlinear ограничений выберите double_ineq.
Нелинейный алгоритм ограничения вызывает patternsearch чтобы взять много вычислений функции. В разделе Specify solver options щелкните знак плюс справа от текущих параметров, чтобы отобразить дополнительные опции. Затем увеличьте максимальный предел вычисления функции до 5e4.

Еще раз запустите задачу, чтобы перезапустить оптимизацию.
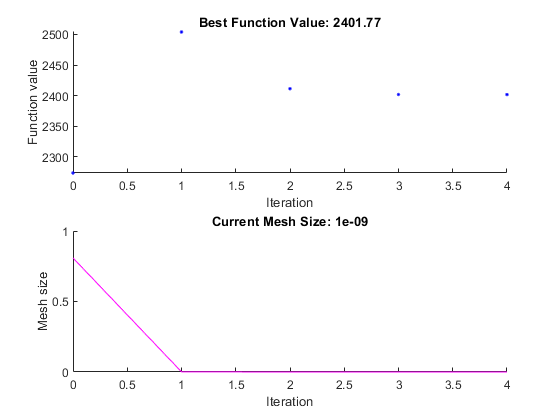
Просмотрите решение и значение целевой функции.
disp(solution)
7.2083
-1.3873
4.9579
-3.1393
-3.1843
4.7457disp(objectiveValue)
2.4018e+03
Значение целевой функции выше, чем значение в задаче без нелинейных ограничений. Предыдущее решение невозможно применительно к нелинейным ограничениям.
Графики показывают много меньше итераций, чем раньше, потому что нелинейный алгоритм ограничения изменяет patternsearch алгоритм для включения другого внешнего контура, чтобы решить измененную задачу. Внешний контур уменьшает изменение задачи при каждой основной итерации. В этом случае алгоритм делает только четыре внешние итерации. Для получения дополнительной информации об алгоритме см. «Нелинейный алгоритм решателя ограничений».
patternsearch в командной строкеЧтобы решить исходную задачу (только линейные ограничения) в командной строке, выполните следующий код.
x0 = [2 1 0 9 1 0]'; options = optimoptions('patternsearch',... 'PollMethod','GSSPositiveBasis2N',... 'PlotFcn',{'psplotbestf','psplotmeshsize'}); lb = []; ub = []; nonlcon = []; [x,fval] = patternsearch(F,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
Optimization terminated: mesh size less than options.MeshTolerance.
x =
8.5165
-6.1094
4.0989
1.2877
-4.2348
2.1812
fval =
1.9195e+03patternsearch генерирует первую пару графиков, показанных в примере задачи Optimize Live Editor.
Чтобы включить нелинейные ограничения, сохраните следующий код в файл с именем double_ineq.m на пути MATLAB.
function [c, ceq] = double_ineq(x) c = [-1.5 + x(1)*x(2) + x(1) - x(2); -x(1)*x(2) - 10]; ceq = []; end
Чтобы позволить решателю запустить к завершению с нелинейными ограничениями, увеличьте допустимое количество вычислений функции.
options.MaxFunctionEvaluations = 5e4;
Решите задачу, включая нелинейные ограничения.
nonlcon = @double_ineq; [x,fval] = patternsearch(F,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
Optimization terminated: mesh size less than options.MeshTolerance
and constraint violation is less than options.ConstraintTolerance.
x =
7.2083
-1.3873
4.9579
-3.1393
-3.1843
4.7457
fval =
2.4018e+03patternsearch также генерирует вторую пару графиков, показанных в примере задачи Optimize Live Editor.
И задача Optimize Live Editor, и командная строка позволяют вам сформулировать и решить задачи, и они дают одинаковые результаты. Командная строка более упорядочена, но предоставляет меньше помощи для выбора решателя, настройки задачи и выбора опций, таких как функции построения графика. Можно также начать задачу с помощью Optimize, а затем сгенерировать код для использования в командной строке, как в Решать Ограниченную Нелинейную Задачу, Основанную на Решателе.