В качестве примера рассмотрим следующую функцию.
Следующий рисунок показывает график функции.
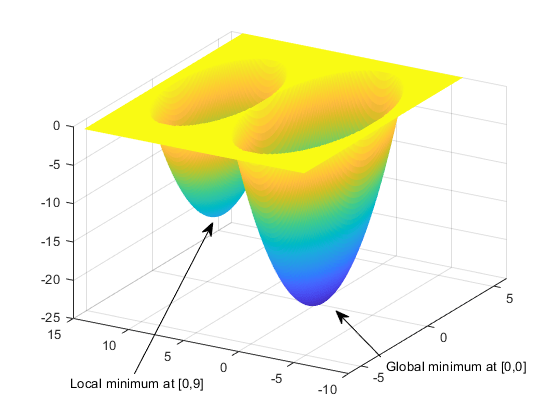
Глобальный минимум функции происходит в (0, 0), где его значение составляет -25. Однако функция также имеет локальный минимум в (0, 9), где ее значение составляет -16.
Чтобы создать файл, который вычисляет функцию, скопируйте и вставьте следующий код в новый файл в MATLAB® Редактор.
function z = poll_example(x) if x(1)^2 + x(2)^2 <= 25 z = x(1)^2 + x(2)^2 - 25; elseif x(1)^2 + (x(2) - 9)^2 <= 16 z = x(1)^2 + (x(2) - 9)^2 - 16; else z = 0; end
Сохраните файл следующим poll_example.m в папке по пути MATLAB.
Чтобы запустить поиск шаблона функции, введите следующее.
options = optimoptions('patternsearch','Display','iter'); [x,fval] = patternsearch(@poll_example,[0,5],... [],[],[],[],[],[],[],options)
MATLAB возвращает таблицу итераций и решение.
x =
0 9
fval =
-16Алгоритм начинается с a = оценки функции в начальной точке, f (0, 5) = 0. Опрос оценивает следующее во время первых итераций.
f ((0, 5) + (1, 0)) = f (1, 5) = 0
f ((0, 5) + (0, 1)) = f (0, 6) = -7
Как только поиск опрашивает точку сетки (0, 6), при которой значение целевой функции меньше, чем в начальной точке, он останавливает опрос текущего mesh и устанавливает текущую точку при следующей итерации равной (0, 6). Следовательно, поиск движется к локальному минимуму на (0, 9) при первой итерации. Вы видите это, глядя на первые две линии отображения командной строки.
Iter f-count f(x) MeshSize Method
0 1 0 1
1 3 -7 2 Successful PollОбратите внимание, что поиск шаблона выполняет только две оценки целевой функции при первой итерации, увеличивая общее количество функций с 1 до 3.
Далее задайте UseCompletePoll на true и повторите оптимизацию.
options.UseCompletePoll = true;
[x,fval] = patternsearch(@poll_example,[0,5],...
[],[],[],[],[],[],[],options);На этот раз поиск шаблона находит глобальный минимум на (0, 0). Различие между этим запуском и предыдущим заключается в том, что с UseCompletePoll установлено на trueПри первой итерации поиск шаблона опрашивает весь четыре сетчатый.
f ((0, 5) + (1, 0)) = f (1, 5) = 0
f ((0, 5) + (0, 1)) = f (0, 6) = -6
f ((0, 5) + (-1, 0)) = f (-1, 5) = 0
f ((0, 5) + (0, -1)) = f (0, 4) = -9
Поскольку последняя точка сетки имеет самое низкое значение целевой функции, поиск по шаблону выбирает его как текущую точку при следующей итерации. Первые две линии командной строки показывают это.
Iter f-count f(x) MeshSize Method
0 1 0 1
1 5 -9 2 Successful PollВ этом случае целевая функция оценивается четыре раза при первой итерации. В результате поиск шаблона движется к глобальному минимуму на (0, 0).
Следующий рисунок сравнивает последовательность точек, возвращаемых, когда Complete poll установлено на Off с последовательностью, когда Complete poll On.
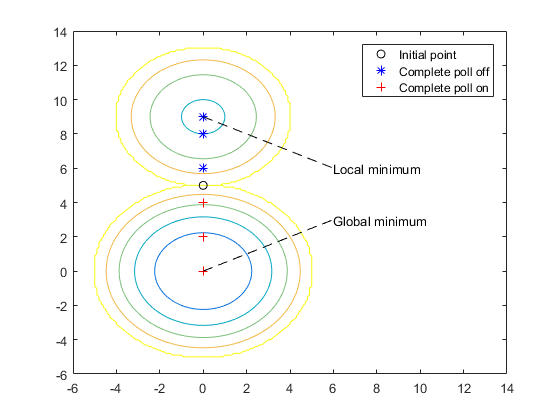
Этот пример показов, как несколько опции опроса взаимодействуют с точки зрения итераций и общих вычислений функции. Основные результаты:
GSS более эффективен, чем GPS или MADS для линейно ограниченных задач.
Задает ли UseCompletePoll на true увеличивает эффективность или уменьшает эффективность неясно, хотя и влияет на количество итераций.
Точно так же имеет ли 2N опрос более или менее эффективен, чем наличие Np1 опрос также неясен. Самый эффективный опрос GSS Positive Basis Np1 с Complete poll установленным значением on. Наименее эффективным является MADS Positive Basis Np1 с Complete poll установленным значением on.
Примечание
Эффективность алгоритма зависит от задачи. GSS эффективен для линейно ограниченных задач. Однако предсказать последствия эффективности других опций опроса трудно, как и знать, какой тип опроса лучше всего работает с другими ограничениями.
Задача та же, что и в Solve Using patternsearch в Optimize Live Editor Task. Эта линейно ограниченная задача использует lincontest7 файл, который поставляется с тулбоксом:
Введите следующее в рабочее рабочее пространство MATLAB.
x0 = [2 1 0 9 1 0]; Aineq = [-8 7 3 -4 9 0]; bineq = 7; Aeq = [7 1 8 3 3 3; 5 0 -5 1 -5 8; -2 -6 7 1 1 9; 1 -1 2 -2 3 -3]; beq = [84 62 65 1];
Установите начальные опции и целевую функцию.
options = optimoptions('patternsearch',... 'PollMethod','GPSPositiveBasis2N',... 'PollOrderAlgorithm','consecutive',... 'UseCompletePoll',false); fun = @lincontest7;
Запустите оптимизацию, назвав output структура outputgps2noff.
[x,fval,exitflag,outputgps2noff] = patternsearch(fun,x0,...
Aineq,bineq,Aeq,beq,[],[],[],options);Установите опции, чтобы использовать полный опрос.
options.UseCompletePoll = true;
Запустите оптимизацию, назвав output структура outputgps2non.
[x,fval,exitflag,outputgps2non] = patternsearch(fun,x0,...
Aineq,bineq,Aeq,beq,[],[],[],options);Продолжите подобным образом, чтобы создать структуры output для других методов опроса с UseCompletePoll установите true и false: outputgss2noff, outputgss2non, outputgssnp1off, outputgssnp1on, outputmads2noff, outputmads2non, outputmadsnp1off, и outputmadsnp1on.
У вас есть результаты 12 запусков оптимизации. Следующая таблица показывает эффективность запусков, измеренную в общем количестве функций и итерациях. Ваши результаты MADS могут отличаться, поскольку MADS является стохастическим алгоритмом.
| Алгоритм | Количество функций | Итерации |
|---|---|---|
| GPS2N, завершите опрос off | 1462 | 136 |
| GPS2N, завершите опрос на | 1396 | 96 |
| GPSNp1, завершите опрос off | 864 | 118 |
| GPSNp1, завершите опрос на | 1007 | 104 |
| GSS2N, завершите опрос off | 758 | 84 |
| GSS2N, завершите опрос на | 889 | 74 |
| GSSNp1, завершите опрос off | 533 | 94 |
| GSSNp1, завершите опрос на | 491 | 70 |
| MADS2N, завершите опрос off | 922 | 162 |
| MADS2N, завершите опрос на | 2285 | 273 |
| MADSNp1, завершите опрос off | 1155 | 201 |
| MADSNp1, завершите опрос на | 1651 | 201 |
Чтобы получить, скажем, первую строку таблицы, введите gps2noff.output.funccount и gps2noff.output.iterations. Можно также изучить опции в редакторе Переменных, дважды щелкнув опции в браузере Рабочей области, а затем дважды щелкнув мышью на output структура.

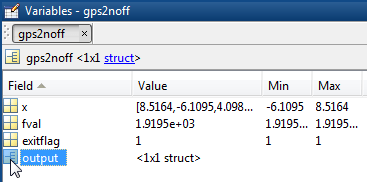
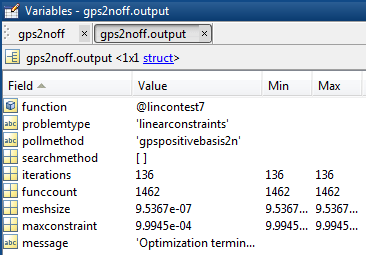
Кроме того, вы можете получить доступ к данным из структур output.
[outputgps2noff.funccount,outputgps2noff.iterations]
ans =
1462 136Основные результаты, извлеченные из таблицы:
Настройка UseCompletePoll на true обычно уменьшает количество итераций для GPS и GSS, но изменение количества вычислений функции непредсказуемо.
Настройка UseCompletePoll на true не обязательно изменяет количество итераций для MADS, но существенно увеличивает количество вычислений функции.
Самые эффективные настройки алгоритма/опций с эффективностью, означающей самое низкое количество функций:
'GSSPositiveBasisNp1' с UseCompletePoll установлено на true (количество функций 491)
'GSSPositiveBasisNp1' с UseCompletePoll установлено на false (количество функций 533)
'GSSPositiveBasis2N' с UseCompletePoll установлено на false (количество функций 758)
'GSSPositiveBasis2N' с UseCompletePoll установлено на true (количество функций 889)
Другие методы опроса имели количество функций, превышающее 900.
Для этой проблемы самый эффективный опрос 'GSSPositiveBasisNp1' с UseCompletePoll установлено на true, хотя и UseCompletePoll установка имеет только небольшое различие. Наименее эффективный опрос 'MADSPositiveBasis2N' с UseCompletePoll установлено на true. В этом случае UseCompletePoll установка имеет существенное различие.