GlobalSearch и MultiStart имеют аналогичные подходы к нахождению глобальных или нескольких минимумов. Оба алгоритма запускают локальный решатель (такой как fmincon) из нескольких начальных точек. Алгоритмы используют несколько начальных точек, чтобы дискретизировать несколько областей притяжения. Для получения дополнительной информации смотрите Области притяжения.
Обзор алгоритмов GlobalSearch и MultiStart содержит эскиз GlobalSearch и MultiStart алгоритмы.
Обзор алгоритмов GlobalSearch и MultiStart
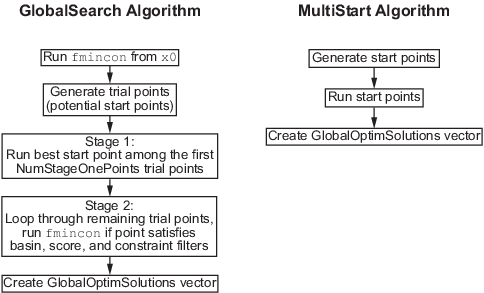
Основные различия между GlobalSearch и MultiStart являются:
GlobalSearch использует механизм поиска рассеяния для генерации начальных точек. MultiStart использует равномерно распределенные начальные точки в границах или предоставленные пользователем стартовые точки.
GlobalSearch анализирует стартовые точки и отвергает те точки, которые вряд ли улучшат лучший локальный минимум, найденный до сих пор. MultiStart запуски всех начальных точек (или, опционально, всех начальных точек, которые допустимы относительно границ или ограничений неравенства).
MultiStart дает выбор локального решателя: fmincon, fminunc, lsqcurvefit, или lsqnonlin. The GlobalSearch алгоритм использует fmincon.
MultiStart может работать параллельно, распределяя стартовые точки на несколько процессоров для локального решения. Чтобы запустить MultiStart параллельно см. раздел «Как использовать параллельную обработку в Global Optimization Toolbox».
Различия между этими объектами решателя сводятся к следующему решению, на котором использовать:
Использование GlobalSearch наиболее эффективно найти один глобальный минимум на одном процессоре.
Использование MultiStart кому:
Найдите несколько локальных минимумов.
Прокрутка параллельно.
Используйте решатель кроме fmincon.
Тщательно ищите глобальный минимум.
Исследуйте свои собственные стартовые точки.
Описание алгоритма см. в Ugrey et al. [1].
Когда вы run a GlobalSearch объект, алгоритм выполняет следующие шаги:
GlobalSearch запуски fmincon от начальной точки вы даете в problem структура. Если этот запуск сходится, GlobalSearch записывает начальную и конечную точки для начальной оценки по радиусу области притяжения. Кроме того, GlobalSearch записывает окончательное значение целевой функции для использования в функции score (см. «Получение начальной точки этапа 1», «Запуск»).
Функция счета является суммой значения целевой функции в точке и кратной сумме нарушений ограничений. Таким образом, допустимая точка имеет счет, равную ее значению целевой функции. Множественное значение для нарушений ограничений первоначально составляет 1000. GlobalSearch обновляет несколько во время запуска.
GlobalSearch использует алгоритм поиска рассеяния, чтобы сгенерировать набор NumTrialPoints пробные точки. Пробные точки являются потенциальными стартовыми точками. Описание алгоритма поиска рассеяния смотрите в Glover [2]. GlobalSearch генерирует пробные точки в любых конечных границах, которые вы задаете (lb и ub). Неограниченные компоненты имеют искусственные ограничения: lb = -1e4 + 1, ub = 1e4 + 1. Эта область значений не симметрична относительно источник, так что источник не находится в поиске рассеяния. Компоненты с односторонними границами имеют искусственные ограничения, накладываемые на неограниченную сторону, смещенные конечными границами, чтобы сохранить lb < ub.
GlobalSearch оценивает функцию счета набора NumStageOnePoints пробные точки. Затем он принимает точку с лучшим счетом и бежит fmincon с этой точки. GlobalSearch удаляет набор NumStageOnePoints пробные точки из его списка пунктов для рассмотрения.
The localSolverThreshold первоначально является меньшим из двух значений целевой функции в точках решения. Точками решения являются fmincon решения, начиная с x0 и от начальной точки этапа 1. Если обе эти точки решения не существуют или являются недопустимыми, localSolverThreshold первоначально является значением функции штрафа начальной точки этапа 1.
The GlobalSearch эвристическое предположение, что области притяжения являются сферическими. Начальная оценка областей притяжения для точки решения от x0 и точка решения от Стадии 1 являются сферами с центром в точках решения. Радиус каждой сферы является расстоянием от начальной точки до точки решения. Эти предполагаемые умывальные раковины могут перекрываться.
Существует два набора счетчиков, сопоставленных с алгоритмом. Каждый счетчик является количеством последовательных пробных точек, которые:
Лежать в области притяжения. Для каждой умывальной раковины имеется по одному счетчику.
Иметь функцию счета больше localSolverThreshold. Определение счета см. в разделе Запуск fmincon из x0.
Сначала все счетчики равны 0.
GlobalSearch неоднократно исследует оставшуюся пробную точку из списка и выполняет следующие шаги. Он постоянно отслеживает время и останавливает поиск, если прошедшее время превышает MaxTime секунд.
Вызовите пробную точку p. Управляемый fmincon от p если соблюдаются следующие условия:
p не находится ни в одном существующей умывальной раковине. Критерий для каждой умывальной раковины i является:
|p - center(i)| > DistanceThresholdFactor * radius(i).
DistanceThresholdFactor является опцией (значение по умолчанию 0.75).
radius - предполагаемый радиус, который обновляется в Update Basin Radius и порог и реагирует на большие значения счетчика.
счет (p) <localSolverThreshold.
(необязательно) p удовлетворяет связанным и/или ограничениям неравенства. Этот тест происходит, если вы устанавливаете StartPointsToRun свойство GlobalSearch объект к 'bounds' или 'bounds-ineqs'.
Счетчики сброса
Установите счетчики для умывальных раковин и порога равными 0.
Обновление набора решений
Если fmincon выполняется начиная с p, это может привести к положительному выходному флагу, который указывает на сходимость. В этом случае GlobalSearch обновляет вектор GlobalOptimSolution объекты. Вызовите точку решения xp и значение целевой функции fp. Существует два случая:
Для каждой другой точки решения xq со значением целевой функции fq,
|xq - xp| > XTolerance * max(1,|xp|)
или
|fq - fp| > FunctionTolerance * max(1,|fp|).
В этом случае GlobalSearch создает новый элемент в векторе GlobalOptimSolution объекты. Для получения дополнительной информации, содержащейся в каждом объекте, смотрите GlobalOptimSolution.
Для некоторых других xq точек решения со значением целевой функции fq,
|xq - xp| <= XTolerance * max(1,|xp|)
и
|fq - fp| <= FunctionTolerance * max(1,|fp|).
В этом случае GlobalSearch с уважением xp как эквивалентный xq. The GlobalSearch алгоритм изменяет GlobalOptimSolution от xq путем добавления p в массив ячеек X0 точки.
Существует одна незначительная подстройка, которая может произойти с этим обновлением. Если выходной флаг для xq больше 1, и выходной флаг для xp является 1, затем xp заменяет xq. Эта замена может привести к тому, что некоторые точки в той же умывальной раковине будут больше, чем расстояние XTolerance от xp.
Обновление радиуса умывальной раковины и порога
Если выходной флаг тока fmincon прогон положительный:
Установите пороговое значение баллов балла в начальной точке p.
Установите радиус умывальной раковины для xp равен максимуму существующего радиуса (если он имеется) и расстоянию между p и xp.
Отчет для итерационного отображения
Когда GlobalSearch Display свойство 'iter', каждая точка, который fmincon запуски создает одну линию в GlobalSearch итеративное отображение.
Счетчики обновлений
Увеличьте счетчик для каждой умывальной раковины, содержащей p. Сбросьте счетчик каждой другой умывальной раковины в 0.
Увеличьте пороговый счетчик, если счет (p) > = localSolverThreshold. В противном случае сбросьте счетчик на 0.
Реакция на большие значения счетчика
Для каждой умывальной раковины с счетчиком, равным MaxWaitCycle, умножить радиус умывальной раковины на 1 – BasinRadiusFactor. Сбросьте счетчик в 0. (Оба MaxWaitCycle и BasinRadiusFactor являются установившимися свойствами GlobalSearch объект.)
Если пороговый счетчик равен MaxWaitCycle, увеличить порог:
новый порог = порог + PenaltyThresholdFactor* (1 + abs (порог)).
Сбросьте счетчик в 0.
Отчет для итерационного отображения
Каждая 200-я пробная точка создает одну линию в GlobalSearch итеративное отображение.
После достижения MaxTime секунд или истечения пробных точек, GlobalSearch создает вектор GlobalOptimSolution объекты. GlobalSearch упорядочивает вектор по значению целевой функции от самого низкого (лучший) до самого высокого (худший). На этом алгоритм завершается.
Когда вы run a MultiStart объект, алгоритм выполняет следующие шаги:
MultiStart проверяет входные аргументы для валидности. Проверки включают запуск локального решателя один раз на входах задачи. Даже при параллельном запуске MultiStart выполняет эти проверки последовательно.
Если вы звоните MultiStart с синтаксисом
[x,fval] = run(ms,problem,k)
для целого числа k, MultiStart генерирует k - 1 стартовые точки точно так же, как если бы вы использовали RandomStartPointSet объект. Алгоритм также использует x0 начальная точка от problem структура, на общую сумму k начальные точки.
A RandomStartPointSet объект не имеет точек, сохраненных внутри объекта. Вместо этого MultiStart вызовы list, который генерирует случайные точки в границах, заданных problem структура. Если существует неограниченный компонент, list использует искусственную границу, заданную ArtificialBound свойство RandomStartPointSet объект.
Если вы предоставляете CustomStartPointSet объект, MultiStart не генерирует начальные точки, но использует точки в объекте.
Если вы задаете StartPointsToRun свойство MultiStart объект к 'bounds' или 'bounds-ineqs', MultiStart не запускает локальный решатель из недопустимых начальных точек. В этом контексте «недопустимые» означают стартовые точки, которые не удовлетворяют границам, или стартовые точки, которые не удовлетворяют и границам, и ограничениям неравенства.
Настройка по умолчанию StartPointsToRun является 'all'. В этом случае MultiStart не отбрасывает недопустимые начальные точки.
MultiStart запускает локальный решатель, указанный в problem.solver, начиная с точек, которые проходят StartPointsToRun фильтр. Если MultiStart работает параллельно, отправляет начальные точки рабочим процессорам по одному, а рабочие процессоры запускают локальный решатель.
Локальный решатель проверяет, MaxTime ли секунды прошли в каждой из его итераций. Если это так, он выходит из этой итерации, не сообщая о решении.
Когда локальный решатель останавливается, MultiStart сохраняет результаты и переходит к следующему шагу.
Отчет по итерационному отображению. Когда MultiStart Display свойство 'iter'каждая точка, которую запускает локальный решатель, создает одну линию в MultiStart итеративное отображение.
MultiStart останавливается, когда заканчиваются начальные точки. Он также останавливается, когда превышает общее время запуска MaxTime секунд.
После MultiStart достигает условия остановки, алгоритм создает вектор GlobalOptimSolution объекты следующим образом:
Сортировка локальных решений по значению целевой функции (Fval) от самого низкого до самого высокого. Для lsqnonlin и lsqcurvefit локальные решатели, целевой функцией является норма невязки.
Закольцовывайте локальные решения j начиная с самого низкого (лучшего) Fval.
Найти все решения k удовлетворяющие обоим:
|Fval(k) - Fval(j)| <= FunctionTolerance*max(1,|Fval(j)|)
|x(k) - x(j)| <= XTolerance*max(1,|x(j)|)
Запись j, Fval(j), локальный решатель output структура для j, и массив ячеек начальных точек для j и все k. Удалите эти точки k из списка локальных решений. Эта точка является одной записью в векторе GlobalOptimSolution объекты.
Получившийся вектор GlobalOptimSolution объекты в порядке по Fval, от самого низкого (лучшего) до самого высокого (худшего).
Отчет по итерационному отображению. Изучив все локальные решения, MultiStart задает сводные данные для итерационного отображения. Эти сводные данные включают количество локальных запусков решателя, которые сходились, количество, которое не удалось сходиться, и количество, которое имело ошибки.
[1] Угрей, Жолт, Леон Ласдон, Джон К. Пламмер, Фред Гловер, Джеймс Келли и Рафаэль Марти. Рассеяние и локальные решатели NLP: мультистартовая среда для глобальной оптимизации. Журнал ИНФОРМС по вычислению, том 19, № 3, 2007, стр. 328-340.
[2] Glover, F. «A шаблона for scatter search and пути relinking». Искусственная эволюция (Ж.-К. Hao, E.Lutton, E. Ronald, M.Schoenauer, D.Snyers, eds.). Лекции по информатике, 1363, Спрингер, Берлин/Гейдельберг, 1998, стр. 13-54.
[3] Диксон, Л. и Г. П. Сегё. «Глобальная задача оптимизации: введение». К глобальной оптимизации 2 (Dixon, L.C. W. and G.P. Szeg, eds.). Амстердам, Нидерланды: Северная Голландия, 1978.