Векторизация функций «Цель» и «Ограничения»

Векторизация для скорости

Прямой поиск часто запускается быстрее, если вы векторизируете целевые и нелинейные функции ограничения. Это означает, что ваши функции вычисляют все точки в опросе или шаблоне поиска сразу, с одним вызовом функции, без необходимости циклически просматривать точки по одному за раз. Поэтому опция UseVectorized = true работает только тогда, когда UseCompletePoll или UseCompleteSearch также установлено значение true. Однако, когда вы задаете UseVectorized = true, patternsearch проверяет, чтобы цель и любые нелинейные функции ограничения давали выходы правильной формы для векторизованных вычислений, независимо от настройки UseCompletePoll или UseCompleteSearch опции.

Если существуют нелинейные ограничения, целевая функция и нелинейные ограничения все должны быть векторизованы в порядок, чтобы алгоритм вычислял векторизированным образом.

Примечание

Напишите векторизованную целевую функцию или нелинейную ограничительную функцию, чтобы принять матрицу с произвольным числом точек. patternsearch иногда вычисляет одну точку даже во время векторизованного вычисления.

Векторизованная целевая функция

Векторизованная целевая функция принимает матрицу как вход и генерирует вектор значений функции, где каждое значение функции соответствует одной строке или столбцу входной матрицы. patternsearch устраняет неоднозначность в том, представляют ли строки или столбцы матрицы точки шаблона следующим образом. Предположим, что входная матрица имеет m строки и n столбцы:

Если начальная точка x0 является вектор-столбец размера mцелевая функция принимает каждый столбец матрицы как точку в шаблоне и возвращает вектор-строку размера n.
Если начальная точка x0 является вектор-строка размера nцелевая функция принимает каждую строку матрицы как точку в шаблоне и возвращает вектор-столбец размера m.
Если начальная точка x0 является скаляром, patternsearch принимает, что x0 является вектор-строка. Поэтому матрица входа имеет один столбец (n = 1, входная матрица является вектором), и каждая запись матрицы представляет одну строку для вычисляемой целевой функции. Выход целевой функции в этом случае является вектором-столбцом размера m.

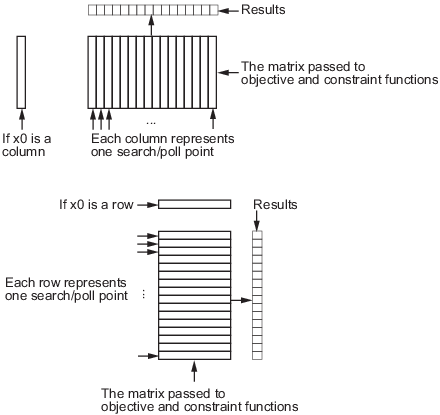
Графически матрица и вычисление представлены следующим рисунком.

Структура векторизованных функций

Например, предположим, что целевая функция является

$f (x) = x_{1}^{4} + x_{2}^{4} - 4 x_{1}^{2} - 2 x_{2}^{2} + 3 x_{1} - x_{2} / 2.$

Если начальный вектор x0 является вектор-столбец, таким как [0;0], функция для векторизованной оценки,

function f = vectorizedc(x)

f = x(1,:).^4+x(2,:).^4-4*x(1,:).^2-2*x(2,:).^2 ...
    +3*x(1,:)-.5*x(2,:);

Если начальный вектор x0 является вектор-строка, таким как [0,0], функция для векторизованной оценки,

function f = vectorizedr(x)

f = x(:,1).^4+x(:,2).^4-4*x(:,1).^2-2*x(:,2).^2 ...
    +3*x(:,1)-.5*x(:,2);

Совет

Если вы хотите использовать ту же целевую функцию (fitness) как для поиска шаблона, так и для генетического алгоритма, напишите свою функцию, чтобы иметь точки, представленные векторами-строками, и напишите x0 как вектор-строка. Генетический алгоритм всегда принимает индивидуумов как строки матрицы. Это было проектом решение - генетический алгоритм не требует предоставляемого пользователем населения, поэтому должен иметь формат по умолчанию.

Чтобы минимизировать vectorizedcвведите следующие команды:

options=optimoptions('patternsearch','UseVectorized',true,'UseCompletePoll',true);
x0=[0;0];
[x,fval]=patternsearch(@vectorizedc,x0,...
         [],[],[],[],[],[],[],options)

MATLAB^® возвращает следующий выход:

Optimization terminated: mesh size less than options.MeshTolerance.

x =
   -1.5737
    1.0575

fval =
  -10.0088

Векторизованные функции ограничения

Векторизировать нужно только нелинейные ограничения; ограничения и линейные ограничения обрабатываются автоматически. Если существуют нелинейные ограничения, целевая функция и нелинейные ограничения все должны быть векторизованы в порядок, чтобы алгоритм вычислял векторизированным образом.

Те же факторы относятся к ограничительным функциям, что и к целевым функциям: начальная точка x0 определяет тип точек (строка или векторы-столбцы) в опросе или поиске. Если начальная точка является вектором-строкой k размера, матричная x, переданная ограничительной функции, имеет k столбца. Точно так же, если начальная точка является вектор-столбец k размера, матрица точек опроса или поиска имеет k строк. Рисунок Структура векторизованных функций может сделать это ясным. Если начальная точка является скаляром, patternsearch принимает, что это вектор-строка.

Ваша нелинейная функция ограничения возвращает две матрицы, одну для ограничений неравенства и одну для ограничений равенства. Предположим, что существует _nc нелинейных ограничений неравенства и _nceq нелинейных ограничений равенства. Для вектора-строки x0Матрицы ограничений имеют _nc и _nceq столбцов соответственно, и количество строк такое же, как в матрице входа. Точно так же для вектора-столбца x0Матрицы ограничений имеют _nc и _nceq строки соответственно, и количество столбцов такое же, как в матрице входа. В структуре векторизованных функций рисунка «Результаты» включают как _nc, так и _nceq.

Пример векторизованной цели и ограничений

Предположим, что нелинейные ограничения

$\begin{matrix} \frac{x_{1}^{2}}{9} + \frac{x_{2}^{2}}{4} \leq 1 (интерьер эллипса), \\ x_{2} \geq \cosh (x_{1}) - 1. \end{matrix}$

Напишите функцию для этих ограничений для формы строка x0 следующим образом:

function [c ceq] = ellipsecosh(x)

c(:,1)=x(:,1).^2/9+x(:,2).^2/4-1;
c(:,2)=cosh(x(:,1))-x(:,2)-1;
ceq=[];

Минимизируйте vectorizedr (определено в векторизованной целевой функции), удовлетворяющей ограничениям ellipsecosh:

x0=[0,0];
options = optimoptions('patternsearch','UseVectorized',true,'UseCompletePoll',true);
[x,fval] = patternsearch(@vectorizedr,x0,...
         [],[],[],[],[],[],@ellipsecosh,options)

MATLAB возвращает следующий выход:

Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =
   -1.3516    1.0612

fval =
   -9.5394

Документация