Документация

Двумерные фильтры с конечной импульсной характеристикой (КИХ)

Программное обеспечение Image Processing Toolbox™ поддерживает один класс линейного фильтра: двумерный фильтр с конечной импульсной характеристикой (КИХ). Конечная импульсная характеристика имеют конечную степень в одной точке или импульсе. Все функции создания фильтра Image Processing Toolbox возвращают конечная импульсная характеристика.

Конечная импульсная характеристика имеют несколько характеристик, которые делают их идеальными для обработки изображений в MATLAB^® окружение:

Другой класс фильтра, фильтр с бесконечной импульсной характеристикой (БИХ), не так подходит для приложений обработки изображений. Ему не хватает присущей ему стабильности и простоты проекта и реализации конечной импульсной характеристики фильтра. Поэтому этот тулбокс не обеспечивает поддержку БИХ фильтра.

Преобразуйте конечную импульсную характеристику 1-D фильтр в 2-D конечная импульсная характеристика

В этом примере показано, как преобразовать одномерный конечная импульсная характеристика в двумерный конечная импульсная характеристика с помощью ftrans2 функция. Эта функция может быть полезной, потому что легче спроектировать одномерный фильтр с конкретными характеристиками, чем соответствующий двумерный фильтр. Метод частотного преобразования сохраняет большинство характеристик одномерного фильтра, особенно переходную полосу и характеристики пульсации. Форма одномерной частотной характеристики четко видна в двумерной характеристике.

Эта функция использует матрицу преобразования, набор элементов, который задает частотное преобразование. Матрица преобразования этой функции по умолчанию создает фильтры с почти круговой симметрией. Путем определения собственной матрицы преобразования можно получить различные симметрии. (Для получения дополнительной информации см. Jae S. Lim, Двухмерный сигнал и обработка изображений, 1990.)

b = firpm(10,[0 0.4 0.6 1],[1 1 0 0])

b =

  Columns 1 through 9

    0.0537   -0.0000   -0.0916   -0.0001    0.3131    0.4999    0.3131   -0.0001   -0.0916

  Columns 10 through 11

   -0.0000    0.0537

h = ftrans2(b);

h =

  Columns 1 through 9

    0.0001    0.0005    0.0024    0.0063    0.0110    0.0132    0.0110    0.0063    0.0024
    0.0005    0.0031    0.0068    0.0042   -0.0074   -0.0147   -0.0074    0.0042    0.0068
    0.0024    0.0068   -0.0001   -0.0191   -0.0251   -0.0213   -0.0251   -0.0191   -0.0001
    0.0063    0.0042   -0.0191   -0.0172    0.0128    0.0259    0.0128   -0.0172   -0.0191
    0.0110   -0.0074   -0.0251    0.0128    0.0924    0.1457    0.0924    0.0128   -0.0251
    0.0132   -0.0147   -0.0213    0.0259    0.1457    0.2021    0.1457    0.0259   -0.0213
    0.0110   -0.0074   -0.0251    0.0128    0.0924    0.1457    0.0924    0.0128   -0.0251
    0.0063    0.0042   -0.0191   -0.0172    0.0128    0.0259    0.0128   -0.0172   -0.0191
    0.0024    0.0068   -0.0001   -0.0191   -0.0251   -0.0213   -0.0251   -0.0191   -0.0001
    0.0005    0.0031    0.0068    0.0042   -0.0074   -0.0147   -0.0074    0.0042    0.0068
    0.0001    0.0005    0.0024    0.0063    0.0110    0.0132    0.0110    0.0063    0.0024

  Columns 10 through 11

    0.0005    0.0001
    0.0031    0.0005
    0.0068    0.0024
    0.0042    0.0063
   -0.0074    0.0110
   -0.0147    0.0132
   -0.0074    0.0110
    0.0042    0.0063
    0.0068    0.0024
    0.0031    0.0005
    0.0005    0.0001

[H,w] = freqz(b,1,64,'whole');
colormap(jet(64))
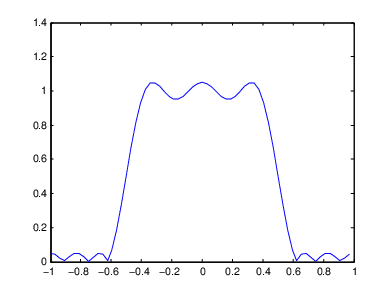
plot(w/pi-1,fftshift(abs(H)))
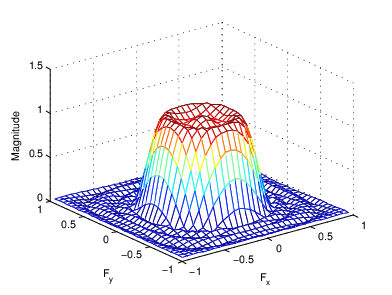
figure, freqz2(h,[32 32])

Метод частотной выборки

Способ частотной дискретизации создает фильтр на основе желаемой частотной характеристики. Учитывая матрицу точек, которые задают форму частотной характеристики, этот метод создает фильтр, частотная характеристика которого проходит через эти точки. Частотная дискретизация не накладывает никаких ограничений на поведение частотной характеристики между заданными точками; обычно реакция пульсирует в этих областях. (Рябь - это колебания вокруг постоянного значения. Частотная характеристика практичного фильтра часто имеет рябь, где частотная характеристика идеального фильтра плоская.)

Функция тулбокса fsamp2 реализует проект частотной выборки для двумерных конечная импульсная характеристика. fsamp2 возвращает h фильтра с частотной характеристикой, которая проходит через точки в матрице входа Hd. В приведенном ниже примере создается фильтр 11 на 11 с использованием fsamp2 и строит график частотной характеристики полученного фильтра. (The freqz2 функция в этом примере вычисляет двумерную частотную характеристику фильтра. Смотрите Вычисление Частотной Характеристики Фильтра для получения дополнительной информации.)

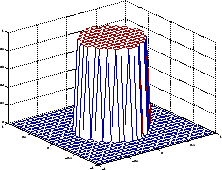
Hd = zeros(11,11); Hd(4:8,4:8) = 1;
[f1,f2] = freqspace(11,'meshgrid');
mesh(f1,f2,Hd), axis([-1 1 -1 1 0 1.2]), colormap(jet(64))
h = fsamp2(Hd);
figure, freqz2(h,[32 32]), axis([-1 1 -1 1 0 1.2])

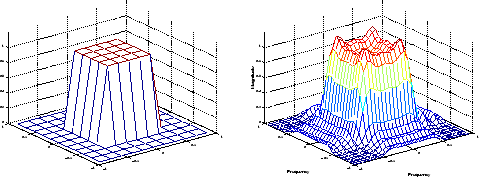
Заметьте рябь в фактической частотной характеристики по сравнению с желаемой частотной характеристикой. Эти рябь являются фундаментальной проблемой с методом проекта частотной выборки. Они происходят везде, где есть резкие переходы в желаемой реакции.

Можно уменьшить пространственную протяженность рябей при помощи большого фильтра. Однако больший фильтр не уменьшает высоту рябей и требует большего времени расчета для фильтрации. Чтобы достичь более плавного приближения к желаемой частотной характеристике, рассмотрите использование метода частотного преобразования или метода оконной обработки.

Метод оконной обработки

Способ оконной обработки включает умножение идеальной импульсной характеристики оконной функцией, чтобы сгенерировать соответствующий фильтр, который сужает идеальную импульсную характеристику. Как и способ частотной дискретизации, способ оконной обработки создает фильтр, частотная характеристика которого аппроксимирует желаемую частотную характеристику. Однако способ оконной обработки имеет тенденцию давать лучшие результаты, чем метод частотной дискретизации.

Тулбокс предлагает две функции для создания фильтра, fwind1 и fwind2. fwind1 проектирует двумерный фильтр с помощью двумерного окна, созданного из одного или двух заданных одномерных окон. fwind2 проектирует двумерный фильтр при помощи заданного двумерного окна непосредственно.

fwind1 поддерживает два различных метода создания двумерных окон, которые он использует:

В приведенном ниже примере используются fwind1 создать фильтр 11 на 11 из желаемой частотной характеристики Hd. Пример использует Signal Processing Toolbox hamming функция для создания одномерного окна, которое fwind1 затем простирается до двумерного окна.

Hd = zeros(11,11); Hd(4:8,4:8) = 1;
[f1,f2] = freqspace(11,'meshgrid');
mesh(f1,f2,Hd), axis([-1 1 -1 1 0 1.2]), colormap(jet(64))
h = fwind1(Hd,hamming(11));
figure, freqz2(h,[32 32]), axis([-1 1 -1 1 0 1.2])

Создание матрицы желательной частотной характеристики

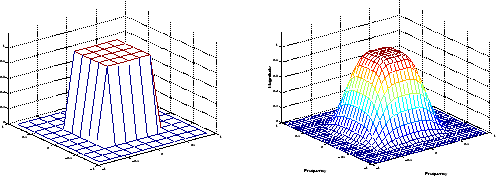
Функции создания фильтра fsamp2, fwind1, и fwind2 все создают фильтры на основе желаемой матрицы величины частотной характеристики. Частотная характеристика является математической функцией, описывающей коэффициент усиления фильтра в ответ на различные входные частоты.

Можно создать соответствующую необходимую матрицу частотной характеристики с помощью freqspace функция. freqspace возвращает правильные, равномерно разнесенные значения частоты для любой размерной характеристики. Если вы создаете необходимую матрицу частотной характеристики, используя частотные точки, отличные от возвращенных freqspace, вы можете получить неожиданные результаты, такие как нелинейная фаза.

Для примера, чтобы создать круговую идеальную частотную характеристику lowpass с отсечкой на 0,5, используйте

[f1,f2] = freqspace(25,'meshgrid');
Hd = zeros(25,25); d = sqrt(f1.^2 + f2.^2) < 0.5;
Hd(d) = 1;
mesh(f1,f2,Hd)

Обратите внимание, что для этой частотной характеристики фильтры, созданные fsamp2, fwind1, и fwind2 реальны. Этот результат желателен для большинства приложений обработки изображений. Чтобы достичь этого в целом, желаемая частотная характеристика должна быть симметричной относительно источника (f1 = 0, f2 = 0).

Вычисление частотной характеристики фильтра

The freqz2 функция вычисляет частотную характеристику для двумерного фильтра. Не имея выходных аргументов, freqz2 создает сетчатый график частотной характеристики. Для примера рассмотрим эту конечную импульсную характеристику фильтр,

h =[0.1667    0.6667    0.1667
    0.6667   -3.3333    0.6667
    0.1667    0.6667    0.1667];

Эта команда вычисляет и отображает частотную характеристику 64 на 64 точек h.

freqz2(h)

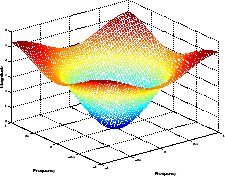
Чтобы получить матрицу частотной характеристики H и векторы частотной точки f1 и f2, используйте выходные аргументы

[H,f1,f2] = freqz2(h);

freqz2 нормализует частоты f1 и f2 так, что значение 1.0 соответствует половине частоты дискретизации, или

Для простого m-by- n ответ, как показано выше, freqz2 использует двумерную функцию быстрого преобразования Фурье fft2. Можно также задать векторы произвольных частотных точек, но в этом случае freqz2 использует более медленный алгоритм.

Смотрите Преобразование Фурье для получения дополнительной информации о быстром преобразовании Фурье и его применении к линейной фильтрации и созданию фильтра.