В integral image каждый пиксель является суммированием пикселей выше и налево от него.
Для иллюстрации ниже показаны и изображение, и соответствующее ему интегральное изображение. Интегральное изображение заполнено налево и сверху, чтобы позволить вычисление. Значение пикселя в (2,1) в оригинальное изображение становится значением пикселя (3,2) в интегральном изображении после добавления значения пикселя выше него (2 + 1) и налево (3 + 0). Точно так же пиксель в (2,2) в оригинальное изображение со значением 4 становится пикселем в (3,3) в интегральном изображении со значением, 12 после добавления пикселя над ним (4 + 5) и добавления пикселя слева от него ((9 + 3).
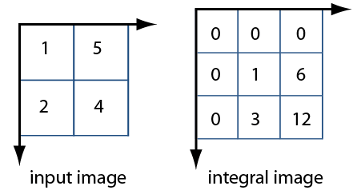
Используя интегральное изображение, можно быстро вычислить суммации по субрегионам изображений. Интегральные изображения облегчают суммирование пикселей и могут выполняться за постоянное время, независимо от размера окрестности. Следующий рисунок иллюстрирует суммирование субрегиона изображения, можно использовать соответствующую область его интегрального изображения. Например, на входном изображении ниже суммирование затененной области становится простым вычислением с использованием четырех ссылочных значений прямоугольной области в соответствующем интегральном изображении. Вычисление становится, 46 - 22 - 20 + 10 = 14. Вычисление вычитает области выше и слева от затененной области. Площадь перекрытия складывается назад, чтобы компенсировать двойное вычитание.
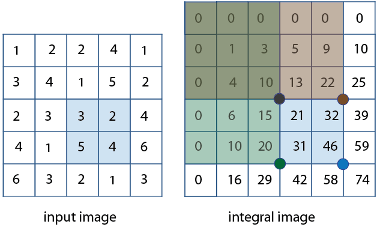
Таким образом, можно быстро вычислять суммирования в прямоугольных областях, независимо от размера фильтра. Использование интегральных изображений было популяризировано алгоритмом Виолы-Джонса. Чтобы увидеть полное цитирование для этого алгоритма и узнать, как создать интегральное изображение, см. integralImage.
integralBoxFilter | integralBoxFilter3 | integralImage | integralImage3