Сигналы синхронизации (PSS и SSS)

В LTE существуют два сигнала синхронизации нисходящей линии связи, которые используются UE для получения тождеств камеры и синхронизации системы координат.

Основной сигнал синхронизации (PSS)
Вторичный сигнал синхронизации (SSS)

Деление в два сигнала направлено на уменьшение сложности процесса поиска камеры.

Тождества камер

Физическая камера тождеств, $N_{I D}^{c e l l}$ , определяется уравнением:

$N_{I D}^{C E L L} = 3 N_{I D}^{(1)} + N_{I D}^{(2)}$

$N_{I D}^{(1)}$ - физический слой камеры тождеств группы (от 0 до 167).
$N_{I D}^{(2)}$ - тождества внутри группы (от 0 до 2).

Эта схема создает 504 уникальные физические единичные камеры.

Сигналы синхронизации и определение тождеств камеры

Основной сигнал синхронизации (PSS) связан с тождествами камеры в группе ( $N_{I D}^{(2)}$ ). Вторичный сигнал синхронизации (SSS) соединяется с группой камеры тождеств ( $N_{I D}^{(1)}$ ) и тождества камеры в группе ( $N_{I D}^{(2)}$ ).

Вы можете получить $N_{I D}^{(2)}$ путем успешной демодуляции PSS. Затем SSS может быть демодулирована и объединена со знанием о $N_{I D}^{(2)}$ получить $N_{I D}^{(1)}$ . Как только вы устанавливаете значения $N_{I D}^{(1)}$ и $N_{I D}^{(2)}$ , можно определить тождества камеры ( $N_{I D}^{c e l l}$ ).

Основной сигнал синхронизации (PSS)

Основной сигнал синхронизации (PSS) основан на частотном диапазоне Последовательности Задова-Чу.

Последовательности Задова-Чу

Последовательности Задова-Чу являются построением последовательностей Франка-Задофа, заданных D. C. Чу в [1]. Эти коды имеют полезное свойство иметь нулевую циклическую автокорреляцию при всех ненулевых лагах. При использовании в качестве кода синхронизации корреляция между идеальной последовательностью и полученной последовательностью наибольшая, когда задержка равна нулю. Когда существует какая-либо задержка между двумя последовательностями, корреляция равна нулю. Это свойство проиллюстрировано на этом рисунке.

Генерация PSS

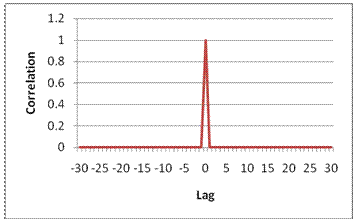
PSS является последовательностью сложных символов, длиной 62 символа.

Последовательность $d_{u} (n)$ используется для PSS, генерируется согласно этим уравнениям:

$d_{u} (n) = e^{- j \frac{π u n (n + 1)}{63}}, для n = 0, 1, \dots, 30$

$d_{u} (n) = e^{- j \frac{π u (n + 1) (n + 2)}{63}}, для n = 31, 32, \dots, 61$

В предыдущем уравнении u является индексом корневой последовательности Задоффа-Чу и зависит от тождеств камеры в группе $N_{I D}^{(2)}$ .

$N_{I D}^{(2)}$	Корневой индекс u
0	25
1	29
2	34

Отображение PSS

PSS преобразуется в первые 31 поднесущие с каждой стороны поднесущей постоянного тока. Поэтому PSS использует шесть ресурсных блоков с пятью зарезервированными поднесущими на каждой стороне, как показано на этом рисунке.

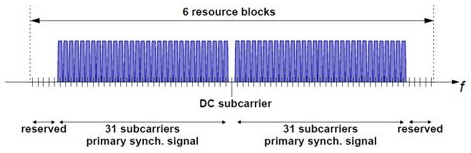
Поскольку поднесущая постоянного тока не содержит информации в LTE, это соответствует отображению на средние 62 поднесущих в символе OFDM в ресурсной сетке. d (n) преобразуется из самой низкой поднесущей в самую высокую поднесущую. PSS преобразуется в различные символы OFDM в зависимости от типа используемой системы координат. Тип системы координат 1 является дуплексом частотного деления (FDD), а тип системы координат 2 является дуплексом временного деления (TDD ).

FDD - PSS преобразуется в последний символ OFDM в пазах 0 и 10, как показано на этом рисунке.
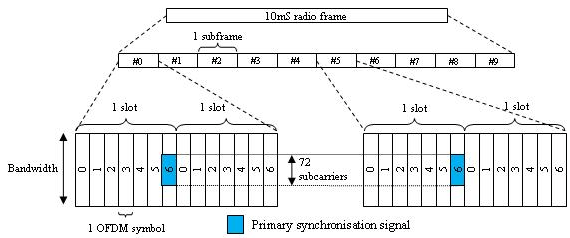
TDD - PSS преобразуется в третий символ OFDM в подкадрах 1 и 6, как показано на этом рисунке.

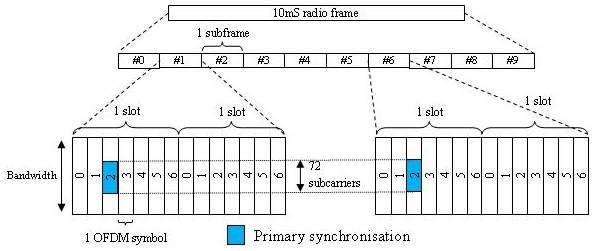
Вторичный сигнал синхронизации (SSS)

Вторичный сигнал синхронизации (SSS) основан на последовательностях максимальной длины (m -последовательности).

M -Определение компонента

m-sequence является псевдослучайной двоичной последовательностью, которая может быть создана путем циклирования через каждое возможное состояние регистра сдвига длины m, получая последовательность длины 2^m–1. Три m, каждый из которых имеет длину 31, используются, чтобы сгенерировать сигналы синхронизации, обозначенные $\tilde{s}$ , $\tilde{c}$ и $\tilde{z}$ .

Генерация SSS

Две двоичные последовательности, каждая длиной 31, используются для генерации SSS. Последовательности s 0^(m₀) и s 1^(m₁) являются различными циклическими сдвигами m -последовательности , $\tilde{s}$ . Индексы m 0 и _m 1 получают из единичной группы ячеек, _NID⁽²⁾ и определите циклический сдвиг. Значения можно считать из таблицы 6.11.2.1-1 в [2].

Две последовательности скремблируются с помощью двоичного кода скремблирования (c 0 (n), c 1 (n)), который зависит от NID⁽²⁾.

Вторая последовательность SSS, используемая в каждой радиостанции системы координат, скремблируется двоичным кодом скремблирования (z 1^(m₀), <reservedrangesplaceholder0> 1^(m₁)), соответствующее значению циклического сдвига первой последовательности, переданной в радиочастотной системе координат.

Генерация двоичной последовательности

Последовательности s 0^(m₀) и s 1^(m₁) заданы этими уравнениями:

$s_{0}^{(m_{0})} (n) = \tilde{s} ((n + m_{0}) mod 31)$

$s_{1}^{(m_{1})} (n) = \tilde{s} ((n + m_{1}) mod 31)$

$\tilde{s}$ сгенерирован из примитивного полинома $x^{5} + x^{2} + 1$ по конечному полю GF (2 ).

c 0 (n) и c 1 (n заданы этими уравнениями:

$c_{0} (n) = \tilde{c} ((n + N_{ID}^{(2)}) mod 31)$

$c_{1} (n) = \tilde{c} ((n + N_{ID}^{(2)} + 3) mod 31)$

$\tilde{c}$ сгенерирован из примитивного полинома $x^{5} + x^{3} + 1$ по конечному полю GF (2 ).

<reservedrangesplaceholder0> 1^(m₀) и z 1^(m₁) заданы этими уравнениями:

$z_{1}^{(m_{0})} (n) = \tilde{z} ((n + (m_{0} mod 8)) mod 31)$

$z_{1}^{(m_{1})} (n) = \tilde{z} ((n + (m_{1} mod 8)) mod 31)$

$\tilde{z}$ сгенерирован из примитивного полинома $x^{5} + x^{4} + x^{2} + x + 1$ по конечному полю GF (2 ).

Отображение SSS

Скремблированные последовательности чередуются, чтобы чередовать последовательность, переданную в первой и второй передаче SSS в каждой радиостанции системы координат. Это позволяет приемнику определять синхронизацию системы координат из наблюдения только одной из двух последовательностей; если первый наблюдаемый сигнал SSS находится в подкадре 0 или подкадре 5, синхронизация может быть достигнута, когда сигнал SSS наблюдается в подкадре 0 или подкадре 5 следующие системы координат.

Как и в случае PSS, SSS преобразуется в различные символы OFDM в зависимости от типа используемой системы координат:

FDD - SSS передается в том же субкадре, что и PSS, но один символ OFDM ранее. SSS преобразуется в те же поднесущие (средние 72 поднесущих), что и PSS.
TDD - SSS преобразуется в последний символ OFDM в пазах 1 и 11, который является тремя символами OFDM перед PSS.

SSS создается с использованием различных последовательностей скремблирования при отображении на четные и нечетные элементы ресурса.

Даже ресурсные элементы:
- Подкадр 0: $d (2 n) = s_{0}^{(m_{0})} (n) c_{0} (n)$
- Субкадр 5: $d (2 n) = s_{1}^{(m_{1})} (n) c_{0} (n)$
Нечетные ресурсные элементы:
- Подкадр 0: $d (2 n + 1) = s_{1}^{(m_{1})} (n) c_{1} (n) z_{1}^{(m_{0})} (n)$
- Субкадр 5: $d (2 n + 1) = s_{0}^{(m_{0})} (n) c_{1} (n) z_{1}^{(m_{1})} (n)$

d (n) преобразуется из самой низкой поднесущей в самую высокую поднесущую .

Ссылки

[1] Chu, D. C. «Полифазные коды с хорошими периодическими корреляционными свойствами». IEEE Trans. Inf. Теория. Том 18, № 4, июль 1972, стр. 531-532.

[2] 3GPP TS 36.211. "Evolved Universal Terrestrial Radio Access (E-UTRA); Физические каналы и модуляция ". 3-ья Генерация Партнерский проект; Группа технических спецификаций Радиосеть доступ. URL-адрес: https://www.3gpp.org.

См. также

Документация