Вы знаете, что самый короткий путь между двумя географическими точками является большим кругом. Моряки и авиаторы заинтересованы в минимизации пройденного расстояния, а значит, и времени. Вы также знаете, что линия гребня является путем постоянного курса, естественным средством путешествия. В целом, чтобы следовать по великому круговому пути, придется постоянно изменять курс. Это непрактично. Однако можно аппроксимировать большой путь окружности сегментами линии реванша так, чтобы добавленное расстояние было незначительным, а количество конечно изменялось минимальным.
Удивительно, но для того, чтобы близко приблизиться к расстоянию пути большого круга, требуется очень мало ветвей линии колес.
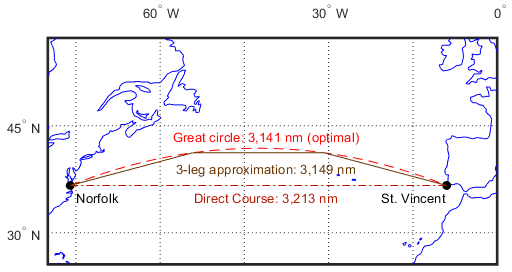
Рассмотрим путешествие из Норфолка, штат Вирджиния (37 ° N, 76 ° W), в мыс Сент-Винсент, Португалия (37 ° N, 9 ° W), один из наиболее сильно распространенных маршрутов в Атлантике. Трасса линии должный-восточный ревень составляет 3 213 морских миль, в то время как оптимальное большое расстояние круга составляет 3 141 морская миля.
Хотя путь линии гребня лишь чуть больше чем на 2% длиннее, это дополнительные 72 мили в течение поездки. Для 12-узлового танкера это приводит к 6-часовой задержке, а в судоходстве время - деньги. Если для аппроксимации большого круга используются всего три сегмента линии гребня, общее расстояние поездки составляет 3 147 морских миль. Наш танкер страдал бы лишь получасовой задержкой по сравнению с непрерывным курсом линии гребня. Вот код для вычисления трех типов треков между Норфолком и Сент-Винсентом:
figure('color','w'); ha = axesm('mapproj','mercator',... 'maplatlim',[25 55],'maplonlim',[-80 0]); axis off, gridm on, framem on; setm(ha,'MLineLocation',15,'PLineLocation',15); mlabel on, plabel on; load coastlines; hg = geoshow(coastlat,coastlon,'displaytype','line','color','b'); % Define point locs for Norfolk, VA and St. Vincent, Portugal norfolk = [37,-76]; stvincent = [37, -9]; geoshow(norfolk(1),norfolk(2),'DisplayType','point',... 'markeredgecolor','k','markerfacecolor','k','marker','o') text(-0.61,0.66,'Norfolk','HorizontalAlignment','left') geoshow(stvincent(1),stvincent(2),'DisplayType','point',... 'markeredgecolor','k','markerfacecolor','k','marker','o') text(0.54,0.66,'St. Vincent','HorizontalAlignment','right') % Compute and draw 100 points for great circle gcpts = track2('gc',norfolk(1),norfolk(2),... stvincent(1),stvincent(2)); geoshow(gcpts(:,1),gcpts(:,2),'DisplayType','line',... 'color','red','linestyle','--') text(-0.02,0.85,'Great circle: 3,141 nm (optimal)',... 'color','r','HorizontalAlignment','center') % Compute and draw 100 points for rhumb line rhpts = track2('rh',norfolk(1),norfolk(2),... stvincent(1),stvincent(2)); geoshow(rhpts(:,1),rhpts(:,2),'DisplayType','line',... 'color',[.7 .1 0],'linestyle','-.') text(-0.02,0.66,'Direct course: 3,213 nm',... 'color',[.7 .1 0],'HorizontalAlignment','center') % Compute and draw path along three waypoints [latpts,lonpts] = gcwaypts(norfolk(1),norfolk(2),... stvincent(1),stvincent(2),3); geoshow(latpts,lonpts,'DisplayType','line',... 'color',[.4 .2 0],'linestyle','-') text(-0.02,0.75,'3-leg approximation: 3,149 nm',... 'color',[.4 .2 0],'HorizontalAlignment','center')
Функция Mapping Toolbox™ gcwaypts вычисляет путевые точки в формате навигационной дорожки в порядок для аппроксимации большого круга с сегментами линии реванша. Он использует этот синтаксис:
[latpts,lonpts] = gcwaypts(lat1,lon1,lat2,lon2,numlegs)
Все входы для этой функции являются скалярами a (начальное и конечное положения). The numlegs вход - это желаемое количество ног равной длины, которое по умолчанию равно 10. Эти выходы векторов-столбцов представляют путевые точки в формате навигационной дорожки ([heading distance]). Размер каждого из этих векторов [(numlegs+1) 1]. Вот точки для этого примера:
[latpts,lonpts] = gcwaypts(norfolk(1),norfolk(2),... stvincent(1),stvincent(2),3) % Compute 3 waypoints
latpts = 37.0000 41.5076 41.5076 37.0000 lonpts = -76.0000 -54.1777 -30.8223 -9.0000
Эти точки представляют путевые точки вдоль большого круга, между которыми аппроксимирующий путь следует по линиям гребня. Четыре очка нужны для трех ног, потому что конечная точка на мысе Сент-Винсент должна быть включена.
Теперь мы можем вычислить расстояние в морских милях (нм) вдоль каждой трассы и через путевые точки:
drh = distance('rh',norfolk,stvincent); % Get rhumb line dist (deg) dgc = distance('gc',norfolk,stvincent); % Get gt. circle dist (deg) % Compute headings and distances for the waypoint legs [course distnm] = legs(latpts,lonpts,'rh');
distrhnm = deg2nm(drh) % Nautical mi along rhumb line distgcnm = deg2nm(dgc) % Nautical mi along great circle distlegsnm = sum(distnm) % Total dist along the 3 legs rhgcdiff = distrhnm - distgcnm % Excess rhumb line distance trgcdiff = distlegsnm - distgcnm % Excess distance along legs
distrhnm =
3.2127e+003
distgcnm =
3.1407e+003
distlegsnm =
3.1490e+003
rhgcdiff =
71.9980
trgcdiff =
8.3446