Аспектом проекции карты является ее ориентация на странице или экране отображения. Если север или юг прямо вверх, то этот аспект называется экваториальным; для большинства проекций это нормальный аспект. Когда центральная ось развивающейся поверхности ориентирована на восток-запад, аспект проекции поперечен. Проекции с центром на Северном полюсе или Южном полюсе имеют полярный аспект, независимо от того, какой меридиан выше. Все другие ориентации имеют наклонный аспект. До сих пор примеры и обсуждения отображения карт фокусировались на нормальном аспекте, безусловно, наиболее часто используемом. В этом разделе рассматривается использование поперечных, косых и косо-косых аспектов. Для получения примера смотрите Управление аспектом проекции карты с вектором ориентации.
Проекционный аспект представляет интерес в первую очередь для отображения карт. Однако в этом разделе также рассматривается, как идея аспекта проекции как преобразования системы координат может быть применена к переменным карты в аналитических целях.
Примечание
Аспект проекции, обсуждаемый в этом разделе, отличается от осей карты Aspect свойство. Карта осей Aspect свойство управляет ориентацией осей рисунка. Например, если карта находится в normal установка с ландшафтной ориентацией, переключение на transverse объект поворачивает оси на 90 °, получая портретную ориентацию. Чтобы отобразить карту в поперечном аспекте, объедините transverse свойство aspect с углом наклона -90 °. Угол наклона является последним элементом Origin параметр. Для примера, a [0 0 -90] вектор будет создавать поперечную карту.
Сопоставление осей Origin свойство является вектором, описывающим геометрию отображаемой проекции. Это свойство Mapping Toolbox™ называется вектором ориентации (предыдущие версии называли его origin vector). Вектор принимает такую форму:
orientvec = [latitude longitude orientation]
Широта и долгота представляют географические координаты центральной точки отображения, из которой вычисляется проекция. Ориентация относится к углу по часовой стрелке от прямого вверх, при котором Северный полюс указывает от этой центральной точки. Вектор ориентации по умолчанию является [0 0 0]; то есть, проектирование сосредоточено на географической точке (0 °, 0 °), и Северный полюс прямой от этой точки. Такое отображение находится в нормальном аспекте. Изменения только на значение долготы вектора ориентации не изменяют аспект; таким образом, нормальный аспект является аспектом с центром на Экваторе в широте с ориентацией 0 °.
Обе эти проекции Миллера имеют нормальные аспекты, несмотря на то, что имеют различные векторы ориентации:
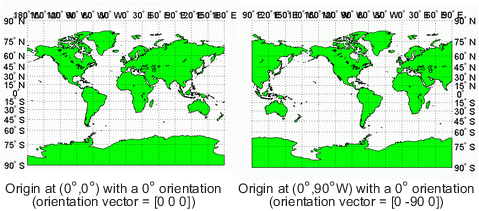
Это имеет смысл, если думать о простой, истинной цилиндрической проекции. Это проекция земного шара на обернутый вокруг него цилиндр. Для нормальных аспектов, этот цилиндр тангенс к шару в Экваторе, и изменение источника долготы просто соответствует вращению сферы вокруг продольной оси цилиндра. Если вы продолжите работу с моделью обернутого цилиндра, можно также понять другие аспекты.
После этого описания поперечный выступ можно рассматривать как цилиндр, обернутый вокруг тангенса земного шара на полюсах и вдоль меридиана и его антиподального меридиана. Наконец, когда такой цилиндр является касательным по любому большому кругу, отличному от меридиана, результатом является наклонная проекция.
Вот схемы четырех цилиндрических ориентаций карты, или аспектов:
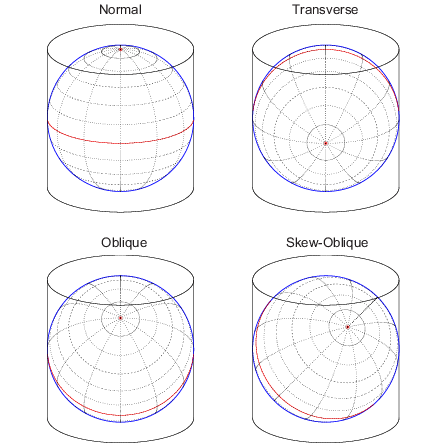
Конечно, несколько выступов являются истинными цилиндрическими выступами, но концепция обернутого цилиндра, тем не менее, является удобным способом описания аспекта.
Пример, в котором используется вектор ориентации, см. в разделе Управление аспектом проекции карты с вектором ориентации.
Лучший способ получить понимание аспекта проекции - экспериментировать с векторами ориентации. В следующем примере используется псевдокилиндрический выступ, синусоидальный.
Создайте оси карты по умолчанию в синусоидальной проекции, включите гратикулу и отобразите набор данных о побережье как заполненные многоугольники. Континенты и гратикула появляются в нормальном аспекте.
figure axesm sinusoid framem on gridm on tightmap tight load coastlines patchm(coastlat,coastlon,'g') title('Normal aspect: orientation vector = [0 0 0]')
![Figure contains an axes. The axes with title Normal aspect: orientation vector = [0 0 0] contains 4 objects of type patch, line.](../examples/map/win64/ExploringProjectionAspectExample_01.png)
Проверьте вектор ориентации от осей карты. По умолчанию источник устанавливается на (0 ° E, 0 ° N), ориентированное на 0 ° от вертикали.
getm(gca,'Origin')ans = 1×3
0 0 0
В нормальном аспекте Северный полюс находится в верхней части изображения. Чтобы создать поперечный аспект, представьте себе тянуть Северный полюс к центру отображения, который изначально был занят точкой (0 °, 0 °). Сделайте это, установив первый элемент Origin параметр до широты 90 ° N. Форма системы координат не влияет. Это все еще синусоидальная проекция.
setm(gca,'Origin',[90 0 0]) title('Transverse aspect: orientation vector = [90 0 0]')
![Figure contains an axes. The axes with title Transverse aspect: orientation vector = [90 0 0] contains 4 objects of type patch, line.](../examples/map/win64/ExploringProjectionAspectExample_02.png)
Нормальный и поперечный аспекты могут быть рассмотрены как ограничивающие условия. Все остальное - косой аспект. Концептуально, если отодвинуть Северный полюс на половину назад в его исходное положение, то есть в положение, первоначально занятое точкой (45 ° N, 0 ° E) в нормальном аспекте, результатом является простой косой аспект. Можно думать об этом как о перетаскивании нового источника (45 ° N, 0 °) к центру изображения, то место, которое (0 °, 0 °) занимало в нормальном аспекте.
setm(gca,'Origin',[45 0 0]) title('Oblique aspect: orientation vector = [45 0 0]')
![Figure contains an axes. The axes with title Oblique aspect: orientation vector = [45 0 0] contains 4 objects of type patch, line.](../examples/map/win64/ExploringProjectionAspectExample_03.png)
Предыдущие примеры проекционного аспекта сохраняли ориентацию аспекта на уровне 0 °. Если вы изменяете ориентацию, наклонный аспект становится наклонно-косой ориентацией. Представьте себе предыдущий пример с ориентацией 45 °. Представьте, что это тянет новый источник (45 ° N, 0 ° E), вниз к центру проекции и затем вращает проекцию, пока Северный полюс не лежит под углом 45 ° по часовой стрелке от прямого вверх относительно нового источника. Как и в предыдущем примере, расположение (45 ° N, 0 ° E) по-прежнему занимает центр карты.
setm(gca,'Origin',[45 0 45]) title('Skew-Oblique aspect: orientation vector = [45 0 45]')
![Figure contains an axes. The axes with title Skew-Oblique aspect: orientation vector = [45 0 45] contains 4 objects of type patch, line.](../examples/map/win64/ExploringProjectionAspectExample_04.png)
Базовая проекция может рассматриваться как стандартная система координат, и ей соответствует нормальный аспект. Функции проекции сохраняются в любом аспекте относительно базовой проекции. Как показано на предыдущих рисунках, контур (система координат) не меняется. Ненаправленные характеристики проекции также не изменяются. Для примера синусоидальная проекция равна площади, независимо от ее аспекта. Однако характеристики направления должны быть рассмотрены тщательно. В нормальном аспекте синусоидальной проекции шкала верна вдоль каждой параллели и центрального меридиана. Это не относится к наклонно-косому аспекту; однако шкала верна вдоль путей преобразованных параллелей и меридиана.
Любая проекция может быть рассмотрена в альтернативных аспектах, и это часто может быть довольно полезно. Например, поперечный аспект проекции Меркатора широко используется в картографии, особенно для отображений с протяженностью преимущественно север-юг. Одним из кандидатов для такого обращения может быть Чили. Косые прогнозы Меркатора могут использоваться для отображения длинных областей, которые не проходят ни на север, ни на юг, ни на восток и запад, таких как Новая Зеландия.