Географический эллипс от центра, больших осей, эксцентриситета и азимута
[lat,lon] = ellipse1(lat0,lon0,ellipse)
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset)
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az)
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az,ellipsoid)
[lat,lon] = ellipse1(___,angleUnit)
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az,ellipsoid,angleUnit,npts)
[lat,lon] = ellipse1(trackStr,...)
mat = ellipse1(...)
[lat,lon] = ellipse1(lat0,lon0,ellipse) вычисляет эллипс с центром (ами) в lat0,lon0. Эллипс определяется третьим входом, который имеет вид [semimajor axis,eccentricity], где входы эксцентриситета могут быть двухэлементным вектором-строкой или двухколоночной матрицей. Эллипсный вход должен иметь одинаковое число строк как вход скаляр или векторы-столбцы lat0 и lon0. Средний вход оси в степени дуги на сфере. Все эллипсы ориентированы так, чтобы их основные оси шли на север-юг.
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset) вычисляет эллипс, где большая ось повернута с должного севера на смещение азимута. The offset угол измеряется по часовой стрелке от должного севера. Если offset = [], тогда смещение не принимается.
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az) использует входную az для определения вычисленных дуг эллипса. Азимуты дуги измеряются по часовой стрелке с должного севера. Если az является вектор-столбец, тогда длина дуги вычисляется с должного севера. Если az является двухколоночной матрицей, затем вычисляются дуги эллипса, начиная с азимута в первом столбце и заканчивая азимутом во втором столбце. Если az = [], затем вычисляется полный эллипс.
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az,ellipsoid) вычисляет эллипс на эллипсоиде, заданный вход ellipsoid. ellipsoid является referenceSphere, referenceEllipsoid, или oblateSpheroid объект или вектор формы [semimajor_axis eccentricity]. Если он опущен, принимается единичная сфера. Когда подается эллипсоид, вход полужидкая ось должна быть в тех же модулях, что и эллипсоидные полужидкие оси. В этом вызове форме модулей оси большой полуоси эллипса не приняты в степени.
[lat,lon] = ellipse1(___,angleUnit) где angleUnit определяет модули входов и выходов. angleUnit можно 'degrees' или 'radians'. Если вы опускаете angleUnit, ellipse1 использует 'degrees'.
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az,ellipsoid,angleUnit,npts) использует скалярную npts для определения числа точек на вычисленный эллипс. Если npts опущен, используются 100 точек.
[lat,lon] = ellipse1(trackStr,...) где trackStr задает либо большую окружность ('gc') или ветряная линия ('rh') расстояния от центра эллипса.
mat = ellipse1(...) возвращает один выходной аргумент, где mat = [lat lon]. Это полезно, если вычисляется только один эллипс.
Можно задать несколько эллипсов с общим центром путем предоставления скалярных lat0 и lon0 входы и двухколоночный ellipse матрица.
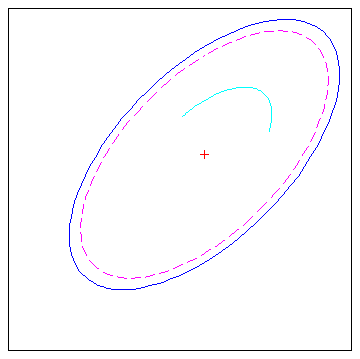
Создайте и постройте график небольшого эллипса с центром (0 °, 0 °), с большой полуосью оси 10 ° и малой полуосью оси 5 °.
axesm mercator ecc = axes2ecc(10,5); plotm(0,0,'r+') [elat,elon] = ellipse1(0,0,[10 ecc],45); plotm(elat,elon)
Если требуемый радиус известен в некоторых модулях неуглового расстояния, используйте радиус, возвращенный earthRadius функционирует как эллипсоидный вход, чтобы задать модули измерения области значений. (Используйте пустую запись азимута, чтобы задать полный эллипс.)
[elat,elon] = ellipse1(0,0,[550 ecc],45,[],earthRadius('nm'));
plotm(elat,elon,'m--')Для всего лишь дуги эллипса введите азимутальную область значений:
[elat,elon] = ellipse1(0,0,[5 ecc],45,[-30 70]); plotm(elat,elon,'c-')