Мапмейкеры разработали сотни проекций карт, за несколько тысяч лет. Три больших семейства проекции карты, плюс несколько небольшие таковые, в целом признаны. Они основаны на типах геометрических форм, которые используются для переноса функций от сферы или сфероида к плоскости. Проекции карты основаны на формируемых поверхностях, и три традиционных семейства состоят из цилиндров, конусов и плоскостей. Они используются для классификации большинства проекций, включая те, которые не построены аналитически (геометрически). В сложение ряд проекций карты основан на многограннике. Хотя многогранные выступы имеют интересные и полезные свойства, они не описаны в этом руководстве.
Какая развиваемая поверхность будет использоваться для проекции, зависит от области, которая должна быть отображена, ее географической протяженности и геометрических свойств, которые должны иметь области, контуры и трассы, с учетом цели карты. В следующих разделах описано и проиллюстрировано, как построены цилиндрические, конические и азимутальные семейства проекций карты, и приведены некоторые примеры проекций, основанных на них.
Цилиндрический выступ получают путем обертывания цилиндра вокруг земного шара, представляющего Землю. Проекция карты - это изображение земного шара, проецируемое на цилиндрическую поверхность, которая затем разворачивается в плоскую поверхность. Когда цилиндр выравнивается по полярной оси, параллели появляются как горизонтальные линии, а меридианы - как вертикальные линии. Цилиндрические выступы могут быть либо равными по площади, либо конформными, либо равноудаленными. Следующие рисунки показывают правильную цилиндрическую или нормальную ориентацию аспекта, в которой цилиндр тангенс к Земле вдоль Экватора, и проекция излучается горизонтально от оси вращения. Метод проекции изображен слева, и пример приведен справа (цилиндрическая проекция равной площади, нормальный/экваториальный аспект).
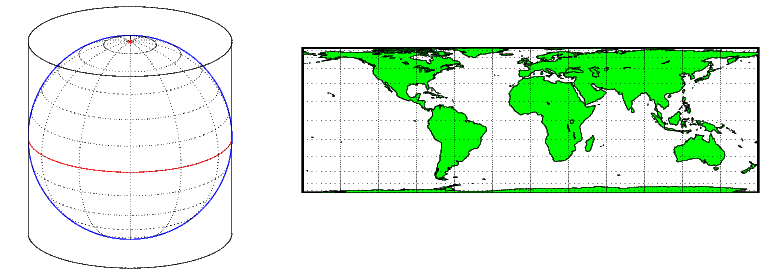
Описание проекционного аспекта смотрите в Projection Aspect.
Некоторые широко используемые цилиндрические проекции карты
Цилиндрический выступ равной площади
Равноудаленный цилиндрический выступ
Проекция Меркатора
Проекция Миллера
Проекция Карре пластины
Универсальная поперечная проекция Меркатора
Все цилиндрические выступы заполняют прямоугольную плоскость. Псевдокилиндрические контуры выступа имеют тенденцию к форме ствола, а не прямоугольной формы. Однако они напоминают цилиндрические проекции с прямыми и параллельными линиями широты и могут иметь равномерно расположенные меридианы, но меридианы являются кривыми, а не прямыми линиями. Псевдокилиндрические выступы могут быть равными по площади, но не конформными или равноудаленными.
Некоторые широко используемые псевдоцилиндрические проекции карты
Проекции Экерта (I-VI)
Гомолозиновая проекция Гуда
Проекция Моллвейда
Квотическая аутентичная проекция
Проекция Робинсона
Синусоидальная проекция
Конический выступ получают из проекции земного шара на размещенный над ним конус. Для нормального аспекта вершина конуса лежит на полярной оси Земли. Если конус касается Земли только одной конкретной параллели широты, он называется тангенсом. Если сделать меньше, конус пересечёт Землю дважды, в этом случае он называется секантом. Конические проекции часто достигают меньших искажений в средних и высоких широтах, чем цилиндрические проекции. Дополнительной разработкой является поликоническая проекция, которая развертывает семейство тангенсирующих или секущих конусов, чтобы скрепить последовательность полос параллелей, чтобы получить еще меньшее искажение шкалы. Следующий рисунок иллюстрирует коническую проекцию, изображающую ее конструкцию слева, с примером справа (проекция Альберса равной площади, полярный аспект).
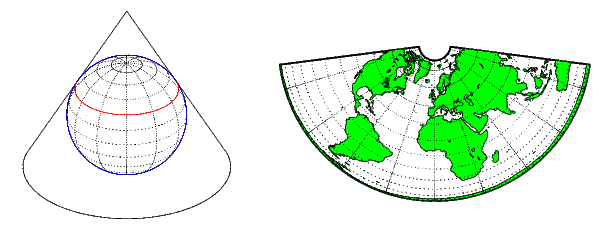
Некоторые широко используемые конические проекции
Albers Проекция равной площади
Равноудаленная проекция
Ламбертская конформная проекция
Поликоническая проекция
Азимутальная проекция является проекцией земного шара на плоскость. В полярном аспекте азимутальная проекция преобразуется в плоскость, касательную к Земле на одном из полюсов, причем меридианы проецируются как прямые линии, излучаемые от полюса, и параллели показаны как полные круги с центром на полюсе. Азимутальные проекции (особенно ортогональные) могут иметь экваториальные или косые аспекты. Проекция сосредоточена на точке, которая находится либо на поверхности, в центре Земли, на антиподе, на некотором расстоянии за пределами Земли, либо в бесконечности. Большинство азимутальных проекций не подходят для отображения всей Земли в одном виде, но дают ощущение земного шара. Следующий рисунок иллюстрирует азимутальную проекцию, изображающую её слева, с примером справа (ортогональная проекция, полярный аспект).
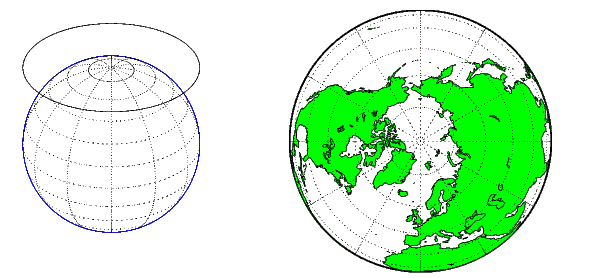
Некоторые широко используемые азимутальные проекции
Равноудаленная азимутальная проекция
Гномоническая проекция
Азимутальная проекция Ламберта равной площади
Ортогональная проекция
Стереографическая проекция
Универсальная полярная стереографическая проекция