Совместимые размеры массивов для основных операций

Большинство двоичных (с двумя входами) операторов и функций в MATLAB^® поддерживает числовые массивы, которые имеют совместимые размеры. Два входа имеют совместимые размеры, если для каждого измерения размерности входов либо одинаковы, либо один из них равен 1. В самых простых случаях два размера массивов совместимы, если они в точности одинаковы или если один скаляр. MATLAB неявно расширяет массивы с совместимыми размерами, чтобы быть одинаковым размером во время выполнения поэлементной операции или функции.

Входы с совместимыми размерами

2-D входы

Это некоторые комбинации скаляров, векторов и матриц, которые имеют совместимые размеры:

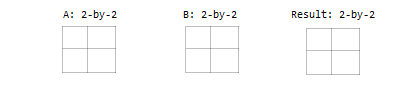
Два входов имеют одинаковый размер.
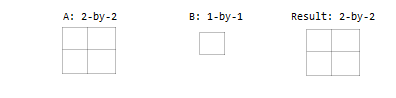
Один вход является скаляром.
Один вход является матрицей, а другой - вектором-столбцом с одинаковым числом строк.
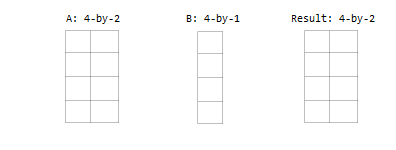
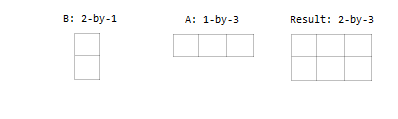
Один вход является вектором-столбцом, а другой - вектор-строка.

Многомерные массивы

Каждый массив в MATLAB имеет последующие измерения размера 1. Для многомерных массивов это означает, что матрица 3 на 4 совпадает с матрицей размера 3 на 4 на 1 на 1 на 1. Примерами многомерных массивов с совместимыми размерами являются:

Один вход является матрицей, а другой - трехмерным массивом с одинаковым числом строк и столбцов.
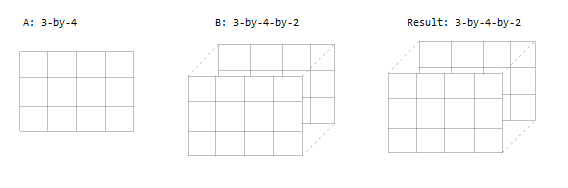
Один вход является матрицей, а другой - трехмерным массивом. Размерности все одинаковые или один из них равен 1.

Пустые массивы

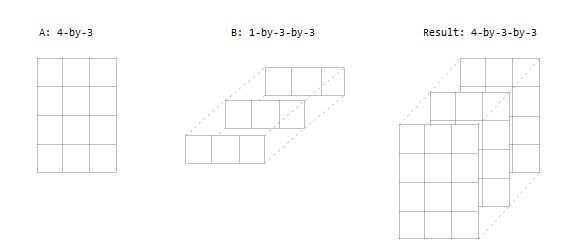
Правила одинаковы для пустых массивов или массивов с нулевым размером размерности. Размер размерности, не равный 1, определяет размер выхода. Это означает, что размерности с нулевым размером должны быть в паре с размерностью 1 или 0 в другом массиве, и что выход имеет размер 0.

     A: 1-by-0     
     B: 3-by-1
Result: 3-by-0

Входы с несовместимыми размерами

Несовместимые входы имеют размеры, которые не могут быть неявно расширены, чтобы быть одинаковыми по размеру. Для примера:

Один из размерности размеров не равен, и ни один из них не равен 1.
```
A: 3-by-2
B: 4-by-2
```
Два нескалярных векторов-строк с длинами, которые не совпадают.
```
A: 1-by-3
B: 1-by-4
```

Примеры

Вычесть вектор из матрицы

Чтобы упростить векторно-матричные операции, используйте неявное расширение с размерными функциями, такими как sum, mean, min, и другие.

Например, вычислите среднее значение каждого столбца в матрице, затем вычитайте среднее значение из каждого элемента.

A = magic(3)

A =

     8     1     6
     3     5     7
     4     9     2

C = mean(A)

C =

     5     5     5

A - C

ans =

     3    -4     1
    -2     0     2
    -1     4    -3

Добавить вектор-строку и вектор

Векторы строка и столбец имеют совместимые размеры, и когда вы выполняете операцию над ними, результатом является матрица.

Для примера добавьте вектор строка и столбец. Результат такой же, как и bsxfun(@plus,a,b).

a = [1 2 3 4]

ans =

     1     2     3     4

b = [5; 6; 7]

a + b

ans =

     6     7     8     9
     7     8     9    10
     8     9    10    11

См. также

bsxfun

Документация