Чтобы определить, какая модель обеспечивает лучшую подгонку для набора данных, используйте графики и статистику в представлениях Model Browser. Чтобы определить оптимальную подгонку, сначала исследуйте графические результаты. Когда вы больше не можете исключить модели подгонки, рассматривая их графически, используйте статистические результаты. Используйте эти инструкции, чтобы помочь оценить модели и определить лучшую подгонку.
Когда основанная на модели калибровка Toolbox™ подходит для зашумленных данных, модель может перегружать или подгонять данные. Во время подгонки тулбокс балансирует смещение и отклонение. Смещение измеряет, насколько хорошо модель соответствует трендам данных. Отклонение и корневая средняя квадратичная невязка (RMSE) измеряют, насколько хорошо модель соответствует данным. RMSE является квадратным корнем отклонения.
Чтобы определить, находится ли модель под или избыточно, учитывайте количество параметров в модели. Когда это число увеличивается, сложность модели тоже. По умолчанию Model-Based Calibration Toolbox использует Гауссову модель процесса (GPM), чтобы соответствовать данным. Если количество параметров в GPM приближается к количеству наблюдений, модель может быть избыточной.
Модель | Описание | Уклон | Дисперсия/RMSE |
|---|---|---|---|
Underfit | Модель не захватывает трендов данных. Модель содержит меньше параметров, чем обосновывают данные. | Высоко | Высоко |
Сверхподгонка | Модель слишком близко подходит к точкам данных, следуя за шумом, скорее захватывая тренд. Модель содержит больше параметров, чем обосновывают данные. | Низко | Низко |
Корневая средняя квадратичная невязка измеряет среднее несовпадение между каждой точкой данных и моделью. Чтобы проверить качество подгонки, начните со значений RMSE. Высокие значения RMSE могут указывать на проблемы. Низкие значения RMSE указывают на близкое соответствие с данными. Если модель точно предсказывает каждую точку данных, то RMSE равен нулю.
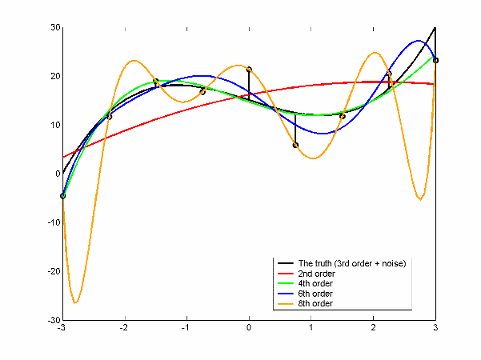
Этот рисунок показывает, как увеличение количества параметров в модели может привести к сверхподбору кривой с сохранением низкого RMSE. Девять «истинных» точек данных сгенерированы из кубического полинома с известным количеством шума. Кубический полином имеет четыре параметра. В этом случае модель 4-го порядка обеспечивает лучшую подгонку.
Модель | Параметры | Сверхподгонка | Underfit | RMSE |
|---|---|---|---|---|
Правда (3-й порядок плюс шум) | 4 | НА | ||
2-й порядок | 3 | ✓ | Высоко | |
4-й порядок | 5 | Низко | ||
6-й порядок | 7 | ✓ | Низко | |
8-й порядок | 9 | ✓ | Низко | |
Если вы полагаетесь исключительно на RMSE, чтобы оценить подгонку модели, модель может быть избыточной и плохо работать в областях, которые не содержат точек данных. Рассмотрите использование предсказанной остаточной суммы ошибок квадратов (PRESS) средней квадратичной невязки (RMSE) и статистики информационных критериев, которые измеряют сверхподгонку модели.
Статистическая величина | Описание | Оценка моделей модели |
|---|---|---|
PRESS RMSE - Предсказанная остаточная сумма ошибок квадратов (PRESS) средняя квадратичная невязка (RMSE) | Для каждой точки данных статистическая величина вычисляет, насколько хорошо модель подходит к точке данных, когда она не включена в подгонку. PRESS RMSE - это среднее значение результатов. | Если PRESS RMSE больше, чем RMSE, модель может оказаться избыточной. В целом используйте PRESS RMSE для небольших наборов данных. |
AIC и AICc - Информационные критерии Акайке BIC - байесовские информационные критерии | Статистика, которая объединяет термин RMSE с термином, который увеличивается с количеством параметров в модели. Это штрафует модель для увеличения ее уровня структуры. AIC, AICc и BIC являются приближениями, которые становятся более точными, когда количество точек данных увеличивается. | Для лучшей подгонки минимизируйте статистику информационных критериев. В целом не используйте их, если отношение точек данных к параметрам не больше 40:1.[1] Используйте AICc для небольших наборов данных. AIC является наиболее подходящим информационным критерием для большинства задач калибровки двигателя. |
Эта статистика помогает вам выбрать модель, которая делает разумные предсказания в точках данных и областях между точками данных. Чтобы подтвердить свою модель, соберите дополнительные данные валидации. Затем используйте свою модель, чтобы измерить, насколько хорошо модель предсказывает эти данные валидации. Сравнение RMSE валидации с RMSE на основе данных моделирования является хорошей статистикой выбора модели. Используйте окно Оценка модели (Model Evaluation), чтобы проверить модели на соответствие другим данным. Можно использовать данные валидации на протяжении плана тестирования.
Чтобы помочь вам использовать информационные критерии для сравнения моделей, в этом разделе представлена справочная информация об информационных критериях Akaike (AIC и AICc) и информационном критерии Байеса (BIC).
Информационные критерии | Описание |
|---|---|
Критерии типа AIC | Основываясь на различии в информации Кулбэка-Лейблера между двумя моделями или их расстоянии K-L. Расстояние K-L является полезной мерой, потому что оно сравнивает информационное содержимое двух кривых путем вычисления энтропии в каждой. Акайке и другие нашли способы оценить расстояние K-L на основе результатов максимальной оценки правдоподобия параметров модели, учитывая некоторые данные. Эти оценки являются информационными критериями и становятся более точными, когда размер выборки увеличивается.[1] |
КОНТРОЛЛЕР МАГИСТРАЛЬНОГО ИНТЕРФЕЙСА | Выведен из теоремы Байеса. Применяет эффект Оккама для выбора предпочтительной модели. Если две модели обеспечивают одинаково хорошую подгонку с некоторыми данными, то более простая модель является likelier. Для моделей с большей сложностью менее примечательно, что они способны хорошо соответствовать заданному набору данных. И наоборот, для простой модели, если вы столкнулись с набором данных, для которого модель обеспечивает приемлемую подгонку, это, казалось бы, совпадение. Поэтому для данных, хорошо совпадающих с обеими моделями, шансы таковы, что более простая из них ближе к истине. [4] |
Факторы Байеса (фактические коэффициенты) | Измерьте относительные вероятности двух моделей. В контексте Model-Based Calibration Toolbox BIC является оценкой факторов Байеса, основанной на результатах максимальной оценки правдоподобия, и, как и AIC, повышает точность в пределе большого размера выборки. Хотя априоры часто приходят на ум в контексте теоремы Байеса, эффект Оккама все еще применяется.[3] |
AIC и BIC улучшаются как оценки своих статистических показателей, когда размер выборки увеличивается, с относительными погрешностями O (n-1), где n - размер выборки. AIC получают из Разложения Тейлора 1-го порядка. AICc является исправлением 2-го порядка для особого случая Гауссова правдоподобия (без общей коррекции 2-го порядка). Используйте AICc, когда отношение выборок данных к параметрам модели (в самой большой модели для вложенных наборов) меньше, чем около 40:1.[2], [5]
Большинство задач в Model-Based Calibration Toolbox не настолько просты, что модель содержит решения динамических уравнений в закрытой форме. Что касается количества выборок на параметр модели, AIC редко может быть надежной статистикой. Вместо этого используйте AICc. Если вы предпочитаете более консервативную оценку сложности модели, рассмотрите использование BIC.
[1] Бернем, Кеннет П. и Дэвид Р. Андерсон. Выбор модели и вывод мультимодели: практический информационно-теоретический подход. 2-е издание. Нью-Йорк: Springer-Verlag, 2002.
[2] Дрейпер, Норман Р и Гарри Смит. Прикладной регрессионный анализ. 3-е издание. Нью-Йорк: John Wiley & Sons, 1998.
[3] Kass, Robert E., and Adrian E. Raftery. «Факторы Байеса». Журнал Американской статистической ассоциации. Том 90, № 430, 1995, с. 773-795.
[4] Леонард, Томас и Джон С. Дж. Хсу. Байесовские методы. Кембридж: Cambridge University Press, 2001.
[5] Маккей, Дэвид. Теория информации, вывод и Алгоритмы обучения. Кембридж: Cambridge University Press, 2003.