В целом решатели берут ограничения с неявной И:
Ограничения 1 И ограничения 2 И ограничения 3 выполняются.
Однако иногда вы хотите ИЛИ:
ограничение 1 ИЛИ ограничение 2 ИЛИ ограничение 3 выполнено.
Эти композиции не являются логически эквивалентными, и обычно нет способа выразить ограничения ИЛИ с точки зрения ограничений И.
Совет
К счастью, нелинейные ограничения чрезвычайно гибки. Вы получаете ограничения OR просто путем установки нелинейной функции ограничения на минимум функций ограничения.
Причина того, что вы можете задать минимум как ограничение, связана с природой Нелинейных Ограничений: вы даете их как набор функций, которые должны быть отрицательными в допустимой точке. Если ваши ограничения
F 1 (x) ≤ 0 OR F 2 (x) ≤ 0 OR F 3 (x) ≤ 0,
затем установите нелинейную функцию ограничения неравенства c (x) как:
c (x) = мин (F 1 (x), F 2 (x), F 3 (x)).
c (x) не является плавным, что является общим требованием к ограничительным функциям, из-за минимума. Тем не менее, метод часто работает.
Примечание
Вы не можете использовать обычные ограничения и линейные ограничения в ограничении OR. Вместо этого преобразуйте ограничения и линейные ограничения в нелинейные функции ограничений, как в этом примере.
Например, предположите, что Ваша выполнимая область - L-образная область: x находится в прямоугольнике-1 <reservedrangesplaceholder4> (1) ≤ 1, 0 ≤ <reservedrangesplaceholder3> (2), ≤ 1 ИЛИ x находится в прямоугольнике 0 <reservedrangesplaceholder1> (1) ≤ 1,-1 ≤ <reservedrangesplaceholder0> (2) ≤ 1.
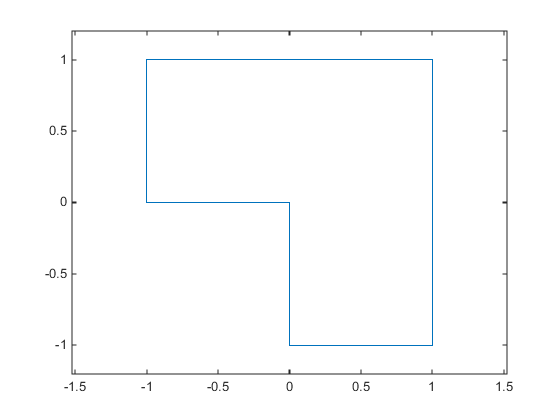
Чтобы представлять прямоугольник как нелинейное ограничение, вместо как связанные ограничения, строят функцию, которая отрицательна в прямоугольнике <reservedrangesplaceholder5> <reservedrangesplaceholder4> (1) ≤ <reservedrangesplaceholder3>, <reservedrangesplaceholder2> ≤ <reservedrangesplaceholder1> (2) ≤ <reservedrangesplaceholder0>:
function cout = rectconstr(x,a,b,c,d) % Negative when x is in the rectangle [a,b][c,d] % First check that a,b,c,d are in the correct order if (b <= a) || (d <= c) error('Give a rectangle a < b, c < d') end cout = max([(x(1)-b),(x(2)-d),(a-x(1)),(c-x(2))]);
Следуя предписанию использования минимума нелинейных ограничительных функций, для L-образной области нелинейная ограничительная функция является:
function [c,ceq] = rectconstrfcn(x) ceq = []; % no equality constraint F(1) = rectconstr(x,-1,1,0,1); % one rectangle F(2) = rectconstr(x,0,1,-1,1); % another rectangle c = min(F); % for OR constraints
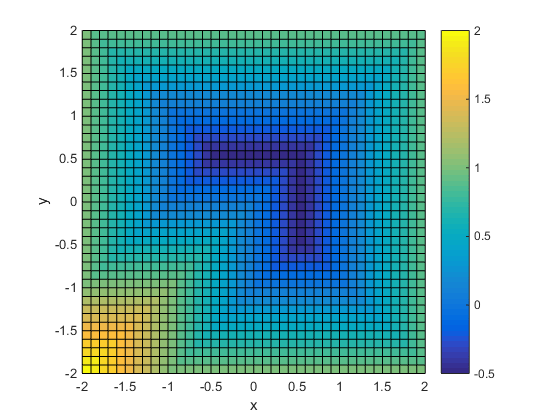
Предположим, что ваша целевая функция
fun = @(x)exp(x(1)) * (4*x(1)^2 + 2*x(2)^2 + 4*x(1)*x(2) + 2*x(2) + 1);
Минимизируйте fun по L-образной области:
opts = optimoptions(@fmincon,'Algorithm','interior-point','Display','off'); x0 = [-.5,.6]; % an arbitrary guess [xsol,fval,eflag] = fmincon(fun,x0,[],[],[],[],[],[],@rectconstrfcn,opts)
xsol =
0.4998 -0.9996
fval =
2.4650e-07
eflag =
1Очевидно, что решение xsol находится внутри L-образной области. Выходной флаг 1, что указывает на то, что xsol является локальным минимумом.