Задайте коэффициенты в приложении PDE Modeler

Коэффициенты для скалярных PDE

Чтобы ввести коэффициенты для вашего УЧП, выберите PDE > PDE Specification.

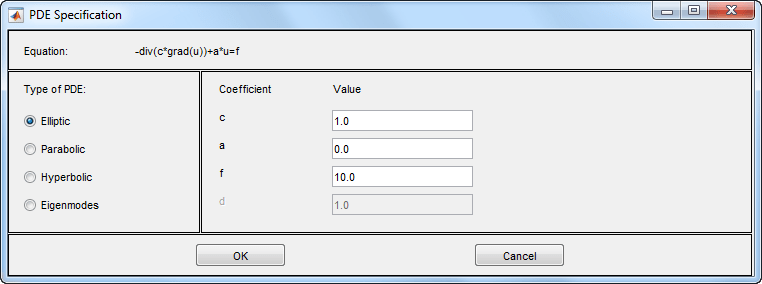
Вводите текстовые выражения с помощью этих соглашений:

x - x -координат
y - y -координат
u - Решение уравнения
ux - Производная u в x -направлении
uy - Производная u в y -направлении
t - Время (параболическое и гиперболическое уравнения)
sd - Число поддомена

Для примера можно использовать это выражение для представления коэффициента:

(x + y)./(x.^2 + y.^2 + 1) + 3 + sin(t)./(1 + u.^4)

Для эллиптических проблем, когда вы включаете u, ux, или uyнеобходимо использовать нелинейный решатель. Выберите Solve > Parameters > Use nonlinear solver.

Примечание

Не используйте кавычки или ненужные пространства в записях. Анализатор может неправильно интерпретировать пространство как вектор диафрагмы, как когда MATLAB^® вектор использует пространство, чтобы разделить элементы массива вектора.
Использование .*, ./, и .^ для операций умножения, деления и экспоненции. Текстовые выражения работают с векторами-строками, поэтому операции должны иметь смысл для векторов-строк. Векторы-строки являются значениями в центроидах треугольника в mesh.

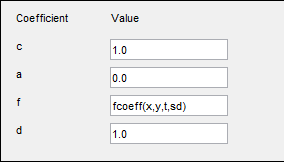
Можно записать функции MATLAB для коэффициентов, а также выражения простого текста. Например, предположим, что ваш коэффициент f задается файлом fcoeff.m.

function f = fcoeff(x,y,t,sd)

f = (x.*y)./(1 + x.^2 + y.^2); % f on subdomain 1
f = f + log(1 + t); % include time
r = (sd == 2); % subdomain 2
f2 = cos(x + y); % coefficient on subdomain 2 
f(r) = f2(r); % f on subdomain 2

Использование fcoeff(x,y,t,sd) как коэффициент f в parabolic решатель.

Коэффициент c является матрицей 2 на 2. Можно задать 1-, 2-, 3- или 4-элементные матричные выражения. Разделите выражения для элементов по пространствам. Эти выражения означают:

1-элементное выражение: $(\begin{matrix} c & 0 \\ 0 & c \end{matrix})$
2-элементное выражение: $(\begin{matrix} c (1) & 0 \\ 0 & c (2) \end{matrix})$
3-элементное выражение: $(\begin{matrix} c (1) & c (2) \\ c (2) & c (3) \end{matrix})$
4-элементное выражение: $(\begin{matrix} c (1) & c (3) \\ c (2) & c (4) \end{matrix})$

Для примера c является симметрической матрицей с постоянными диагональными элементами и cos(xy) как недиагональные условия:

1.1 cos(x.*y) 5.5 (1)

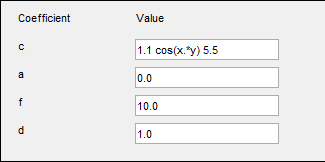
Это соответствует коэффициентам для параболического уравнения

$\frac{\partial u}{\partial t} - \nabla \cdot ((\begin{matrix} 1.1 & \cos (x y) \\ \cos (x y) & 5.5 \end{matrix}) \nabla u) = 10.$

Коэффициенты для систем PDE

Можно ввести коэффициенты для системы с N = 2 уравнения в приложении PDE Modeler. Для этого откройте приложение PDE Modeler и выберите Generic System.

Затем выберите PDE > PDE Specification.

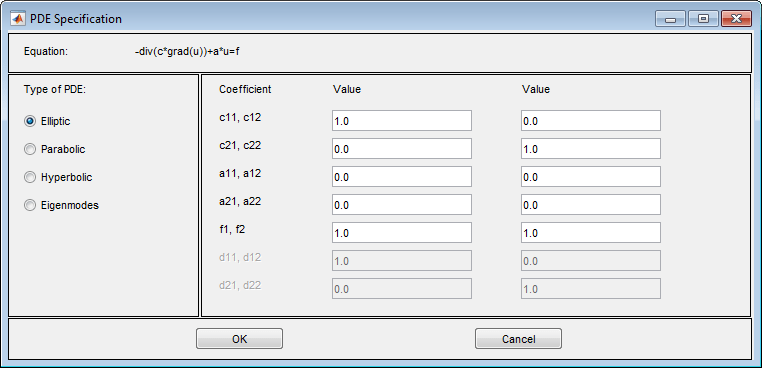
Введите символ выражения для коэффициентов, используя форму в Коэффициенты для Скалярных PDE с дополнительными опциями для нелинейных уравнений. Дополнительные опции:

Представление iпервый компонент решения u использование 'u(i)' для i = 1 или 2.
Точно так же представьте iпервые компоненты градиентов решения u использование 'ux(i)' и 'uy(i)' для i = 1 или 2.

Примечание

Для эллиптических задач, когда вы включаете коэффициенты u(i), ux(i), или uy(i)необходимо использовать нелинейный решатель. Выберите Solve > Parameters > Use nonlinear solver.

Не используйте кавычки или ненужные пространства в записях.

Для систем более высоких размерностей не используйте приложения PDE Modeler. Представьте свои коэффициенты задачи в командной строке.

Можно вводить скаляры в c матрица, соответствующая этим уравнениям:

$\begin{matrix} - \nabla \cdot (c_{11} \nabla u_{1}) - \nabla \cdot (c_{12} \nabla u_{2}) + a_{11} u_{1} + a_{12} u_{2} = f_{1} \\ - \nabla \cdot (c_{21} \nabla u_{1}) - \nabla \cdot (c_{22} \nabla u_{2}) + a_{21} u_{1} + a_{22} u_{2} = f_{2} \end{matrix}$

Если вам нужны матричные версии любого из cij коэффициенты, вводите выражения, разделенные пространствами. Можно задать 1-, 2-, 3- или 4-элементные матричные выражения. Это означает:

1-элементное выражение: $(\begin{matrix} c & 0 \\ 0 & c \end{matrix})$
2-элементное выражение: $(\begin{matrix} c (1) & 0 \\ 0 & c (2) \end{matrix})$
3-элементное выражение: $(\begin{matrix} c (1) & c (2) \\ c (2) & c (3) \end{matrix})$
4-элементное выражение: $(\begin{matrix} c (1) & c (3) \\ c (2) & c (4) \end{matrix})$

Для примера эти выражения показывают один из каждого типа (1-, 2-, 3- и 4-элементные выражения)

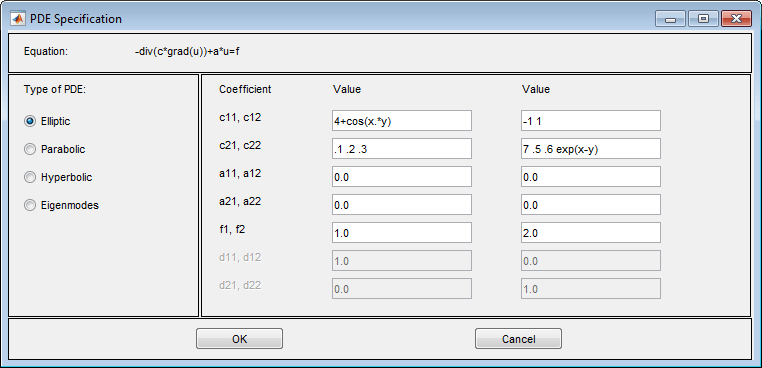
Эти выражения соответствуют уравнениям

$\begin{matrix} - \nabla \cdot ((\begin{matrix} 4 + \cos (x y) & 0 \\ 0 & 4 + \cos (x y) \end{matrix}) \nabla u_{1}) - \nabla \cdot ((\begin{matrix} - 1 & 0 \\ 0 & 1 \end{matrix}) \nabla u_{2}) = 1 \\ - \nabla \cdot ((\begin{matrix} .1 & .2 \\ .2 & .3 \end{matrix}) \nabla u_{1}) - \nabla \cdot ((\begin{matrix} 7 & .6 \\ .5 & \exp (x - y) \end{matrix}) \nabla u_{2}) = 2 \end{matrix}$

Коэффициенты, которые зависят от времени и пространства

В этом примере показано, как ввести зависящие от времени и координат коэффициенты в приложение PDE Modeler.

Решить параболический УЧП,

$d \frac{\partial u}{\partial t} - \nabla \cdot (c \nabla u) + a u = f$

со следующими коэффициентами:

d = 5
a = 0
f - линейный пандус до 10, удерживаемый на 10, затем пандусы назад до 0:
$f = 10 * {\begin{array}{l} 10 t & 0 \leq t \leq 0.1 \\ 1 & 0.1 \leq t \leq 0.9 \\ 10 - 10 t & 0.9 \leq t \leq 1 \end{array}$
c = 1 +. x² + y²

Чтобы решить это уравнение в приложении PDE Modeler, выполните следующие шаги:

Запишите файл framp.m и сохраните его на пути MATLAB.

function f = framp(t)

if t <= 0.1
    f = 10*t;
elseif t <= 0.9
    f = 1;
else
    f = 10-10*t;
end
f = 10*f;

Откройте приложение PDE Modeler при помощи pdeModeler команда.
Отобразить линии сетки можно путем выбора Options > Grid.
Выровнять новые формы по линиям сетки можно путем выбора Options > Snap.
Нарисуйте прямоугольник с углами на (-1, -0.4), (-1,0.4), (1,0,4) и (1, -0.4). Для этого сначала нажмите кнопку. Затем щелкните один из углов левой кнопкой мыши и перетащите мышью, чтобы нарисовать прямоугольник.
Нарисуйте окружность с радиусом 0.2 и центром в (0.5,0). Для этого сначала нажмите кнопку. Затем щелкните правой кнопкой мыши источник и перетащите мышью, чтобы нарисовать круг. Щелчок правой кнопкой мыши ограничивает рисуемую форму так, чтобы она была окружностью, а не эллипсом. Если окружность не является идеальной единичной окружностью, дважды кликните ее. В получившемся диалоговом окне задайте точное центральное положение и радиус окружности.
Моделируйте геометрию путем ввода R1-C1 в поле Set formula.
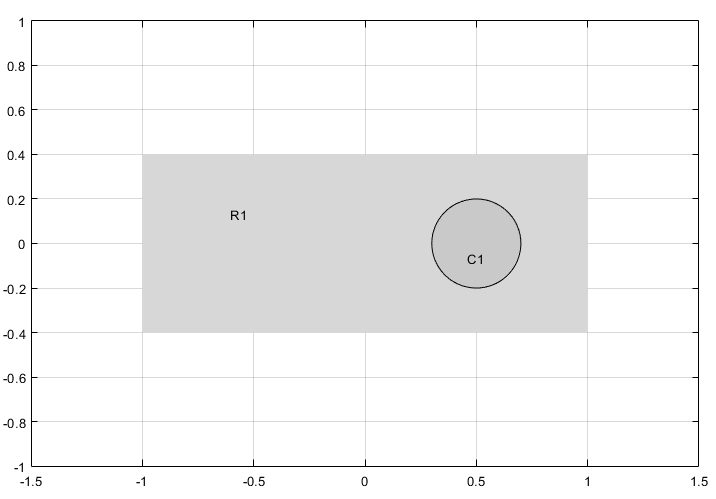
Проверьте, что в прикладном режиме задано Generic Scalar.
Задайте граничные условия. Для этого перейдите в граничный режим путем выбора Boundary > Boundary Mode. Используйте команду Shift + нажатие кнопки, чтобы выбрать несколько контуры. Затем выберите Boundary > Specify Boundary Conditions.
- Для прямоугольника используйте граничное условие Дирихле с h = 1 и r = t*(x-y).
- Для окружности используйте граничное условие Неймана с g = x.^2+y.^2 и q = 1.
Задайте коэффициенты, выбрав PDE > PDE Specification или нажав кнопку PDE на панели инструментов. Выберите тип Parabolic УЧП. Задайте c = 1+x.^2+y.^2, a = 0, f = framp(t), и d = 5.
Примечание
Не включайте кавычки или пространства, когда вы задаете свои коэффициенты в приложении PDE Modeler. Анализатор интерпретирует все входы как векторы символов. Это может неверно истолковать пространство как векторная диафрагма, как когда вектор MATLAB использует пространство, чтобы разделить элементы массива вектора.
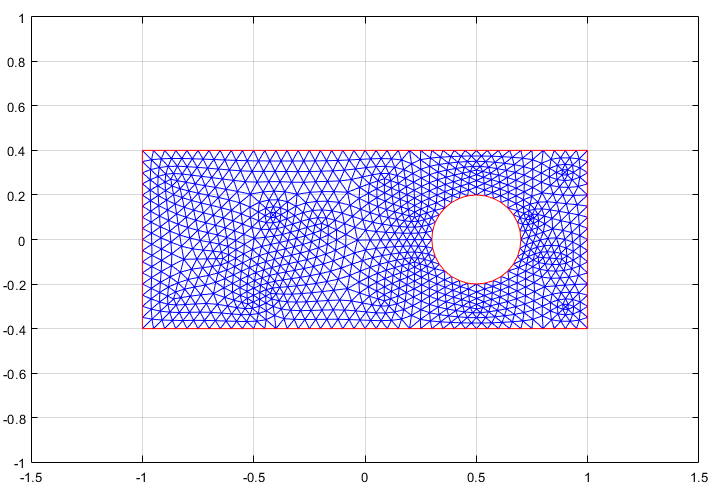
Инициализируйте mesh путем выбора Mesh > Initialize Mesh.
Дважды уточните mesh путем выбора Mesh > Refine Mesh.
Улучшите качество треугольника, выбрав Mesh > Jiggle Mesh.
Установите начальное значение и время решения. Для этого выберите Solve > Parameters.
В получившемся диалоговом окне установите время на linspace(0,1,50) и начальное значение u (_t 0) в 0.
Решить уравнение можно, выбрав Solve > Solve PDE или нажав кнопку = на панели инструментов.
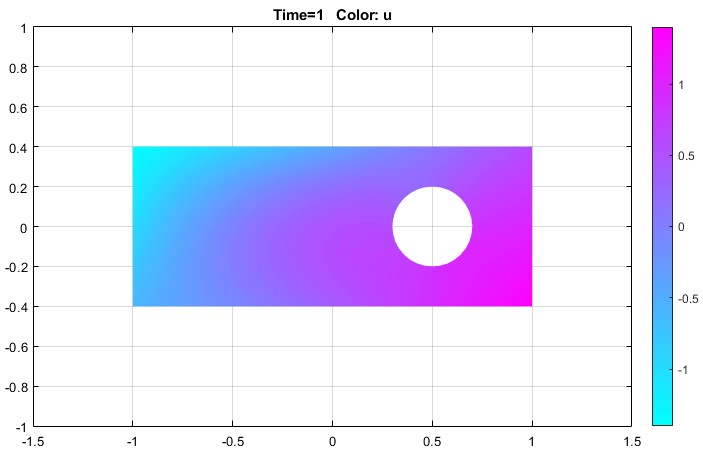
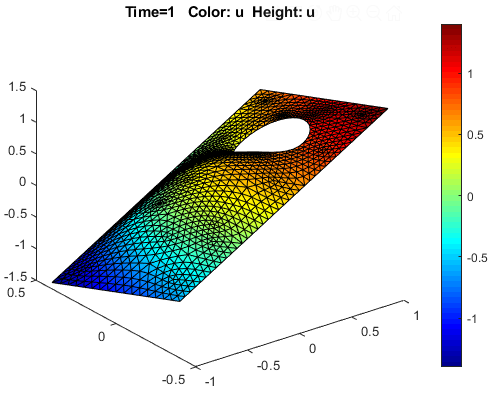
Визуализируйте решение как 3-D статический график. Для этого:
1. Выберите Plot > Parameters.
2. В получившемся диалоговом окне выберите опции Color и Height (3-D plot).
3. Выберите опцию Show mesh.
4. Измените палитру на jet при помощи соответствующего раскрывающегося меню в том же диалоговом окне.

Документация