Глобальная система координат описывает арену, на которой происходит ваша радарная или гидроакустическая симуляция. На этой арене можно разместить радиолокационные или гидроакустические передатчики и приемники, а также цели. Эти объекты могут быть как стационарными, так и перемещающимися. Местоположение и движение этих объектов задается в глобальных координатах.
Можно смоделировать движение всех объектов, используя phased.Platform Системные object™. Этот системный объект вычисляет положение и скорость объектов, используя модели ускорения постоянной скорости или постоянной скорости.
Можно смоделировать сигналы, которые распространяются между объектами в вашем сценарии. Пути луча, которые соединяют передатчики, цели и приемники, заданы в глобальных координатах. Можно распространять сигналы, используя следующие Системные объекты: phased.FreeSpace, phased.WidebandFreeSpace, phased.LOSChannel, или phased.WidebandLOSChannel. Если вы моделируете двухлучевое многолучевое распространение с помощью twoRayChannel (Radar Toolbox), граничная плоскость установлена на z = 0 в глобальной системе координат.
Когда сигналы взаимодействуют с датчиками или целями, взаимодействие почти всегда задается как функция от датчика или локальных координат цели. Локальные системы координат фиксируются к антеннам и микрофонам, фазированным решеткам и целям. Они перемещаются и вращаются вместе с объектом. Локальные координаты обычно адаптируются к форме и симметрии объекта.
Поскольку сигналы распространяются в глобальной системе координат, вы должны иметь возможность преобразовывать локальные координаты в глобальные координаты. Вы делаете это путем построения ортонормальной матрицы осей 3 на 3. Матричные столбцы представляют три вектора ортогонального направления локальных координат, выраженных в глобальной системе координат. Координаты локальной системы координат должны быть ортонормальными, но они не должны быть параллельными глобальным осям координат.
Когда вам нужно вычислить область значений и углы прихода сигнала, вы можете использовать rangeangle функция. Когда вы вызываете эту функцию с положением источника и приемника, выраженными в глобальных координатах, функция возвращает область значений и углы прихода, азимут и повышение относительно осей глобальной системы. Однако, когда вы передаете матрицу ориентации в качестве дополнительного аргумента, азимут и повышение теперь заданы относительно локальной системы координат.
Вы используете локальные координаты, чтобы задать
расположение и ориентация антенных или микрофонных элементов массива. Диаграмма направленности антенной решетки зависит от угла прихода или излучения относительно локальных координат массива.
отраженная энергия от цели является функцией углов падения и отражения относительно локальных осей цели.
Два примера локальных систем координат:
самолет может иметь локальную систему координат с x осью, выровненной вдоль оси фюзеляжа корпуса, и y ось, указывающую вдоль левого крыла. Выберите z -ось, чтобы сформировать правую систему координат.
установленная на транспортном средстве плоская фазированная решетка может иметь локальную систему координат, адаптированную к массиву. Ось x системы координат может указывать вдоль вектора нормали массива.
Следующий рисунок иллюстрирует взаимосвязь локальных и глобальных систем координат в бистатическом радиолокационном сценарии. Толстые сплошные линии представляют координатные оси глобальной системы координат. Существуют две фазированные решетки: передающий равномерный прямоугольный массив (URA) и принимающий URA 5 на 5. Каждый из фазированных решеток содержит свою собственную локальную систему координат. Цель, обозначенная красной стрелой, также содержит локальную систему координат.
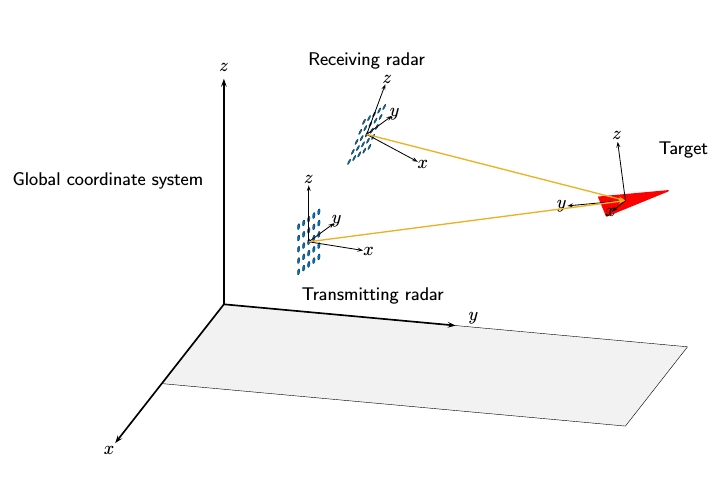
В следующих нескольких разделах рассматриваются локальные системы координат, используемые массивами.
Положения элементов любого Phased Array System Toolbox™ массива всегда заданы в локальной системе координат. При использовании любого из системных объектов, которые создают равномерные массивы, положения элементов массива определяются автоматически относительно предопределенной локальной системы координат. Массивы, для которых это свойство содержит, являются phased.ULA, phased.URA, phased.UCA, phased.HeterogeneousULA, и phased.HeterogeneousURA Системные объекты. Для этих системных объектов массивы описываются с помощью нескольких параметров, таких как интервалы между элементами и количество элементов. Положения элементов затем задаются относительно источника массива, расположенного в (0,0,0), которая является геометрическим центром массива. Геометрический центр является хорошим приближением к центру фазы массива. Центр фазы массива является точкой, от которой излучающие волны, по-видимому, исходят, когда наблюдаются в дальнем поле. Например, для ULA с нечетным числом элементов, элементы расположены на расстояниях (-2d, -d, 0, d, 2d) вдоль оси массива.
Существуют системные объекты массив, для которых необходимо явным образом задать координаты элемента. Можно использовать эти объекты для создания произвольных форм массивов. Эти объекты являются phased.ConformalArray и phased.HeterogeneousConformalArray Системные объекты. Для этих массивов центр фазы массива не должен совпадать с источником массива или геометрическим центром.
Направления Boresight элемента. В дополнение к положениям элементов необходимо задать ориентации элементов, то есть направления, в которых они расположены. Некоторые элементы сильно направлены - большая часть их излучаемой энергии течёт в одном направлении, называемом основной осью отклика (MRA). Другие являются всенаправленными. Ориентация элемента является направлением, указывающим на MRA. Ориентация элемента задается с помощью азимута и повышения в локальной системе координат массива. Направление, с которым сталкивается MRA антенны или микрофона при передаче или приеме сигнала, также называется направлением boresight или look. Для равномерных массивов все направления boresight всех элементов определяются параметрами array. Для конформных массивов вы задаете направление boresight каждого элемента независимо.
Источник массива и центр фазы. Равномерный линейный массив (ULA) является массива элементов антенны или микрофона, которые равноудаленно расположены вдоль прямой линии. В системном Phased Array System Toolbox, phased.ULA Системный объект создает массив ULA. Геометрия ориентации ULA его элементов определяется тремя параметрами: количеством элементов, расстоянием между элементами и ArrayAxis свойство. Для ULA локальная система координат адаптирована к массиву - элементам автоматически присваиваются позиции в локальной системе координат.
Положения элементов массива определяются ArrayAxis свойство, которое может принимать значения 'x', 'y' или 'z'. Свойство оси массива определяет ось, на которой заданы все элементы. Для примера, когда ArrayAxis для свойства задано значение 'x'элементы массива расположены вдоль оси x. Элементы расположены симметрично относительно источника. Поэтому геометрический центр массива лежит в источник системы координат.
Этот рисунок показывает ULA с четырьмя элементами с направленными элементами в локальной правой системе координат. Элементы лежат на оси y с их осями boresight, указывающими на x -направление. В этом случае ArrayAxis для свойства задано значение 'y.
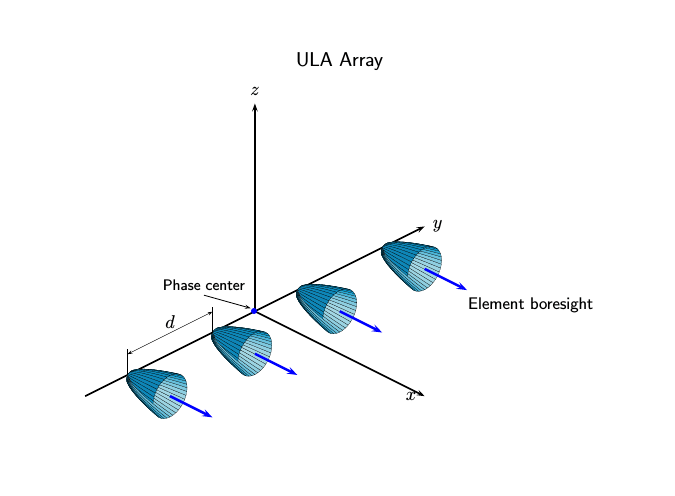
Направление борсайта элемента ULA. В ULA направления boresight каждого элемента указывают в одном направлении. Направление ортогонально оси массива. Это направление зависит от выбора ArrayAxis свойство.
| Значение свойства ArrayAxis | Положения элемента и направления борсайта |
|---|---|
'x' | Элементы массива лежат на оси x. Векторы boresight элемента указывают вдоль оси y. |
'y' | Элементы массива лежат на оси y. Векторы boresight элемента указывают вдоль оси x. |
'z' | Элементы массива лежат на оси z. Векторы boresight элемента указывают вдоль оси x. |
Локальные координаты, адаптированные к равномерному линейному массиву
Создайте два примера равномерного линейного массива и отобразите координаты элементов относительно локальных систем координат, заданных массивами.
Сначала создайте ULA с 4 элементами с интервалом в полуметра.
sULA = phased.ULA('NumElements',4,'ElementSpacing',0.5); ElementLocs = getElementPosition(sULA)
ElementLocs = 3×4
0 0 0 0
-0.7500 -0.2500 0.2500 0.7500
0 0 0 0
viewArray(sULA)

Источник локальной системы координат, ориентированной на массив, устанавливается на центр фазы массива. Центр фазы является средним значением положений элемента массива.
disp(mean(ElementLocs'))
0 0 0
Поскольку массив имеет четное количество элементов, ни один элемент массива не находится в центре фазы (0,0,0).
Затем создайте ULA с 5 элементами с интервалом в тридцать сантиметров.
sULA1 = phased.ULA('NumElements',5,'ElementSpacing',0.3); ElementLocs = getElementPosition(sULA1)
ElementLocs = 3×5
0 0 0 0 0
-0.6000 -0.3000 0 0.3000 0.6000
0 0 0 0 0
viewArray(sULA1)

Поскольку массив имеет нечетное количество элементов в каждой строке и столбце, центральный элемент массива находится в центре фазы.
Источник массива и центр фазы. Равномерный прямоугольный массив (URA) является массива элементов антенны или микрофона, помещённым на регулярную двумерную сетку. Геометрия URA и расположение и ориентация его элементов определяются несколькими параметрами: размерностями массива, расстоянием между элементами и ArrayNormal свойство. Для URA локальная система координат адаптирована к массиву - элементам автоматически присваиваются позиции в локальной системе координат. Источником локальной системы координат является геометрический центр массива. Центр фазы массива совпадает с центром геометрии. Элементы автоматически назначаются положения в этой локальной системе координат. Положения определяются ArrayNormal свойство, которое может принимать значения 'x', 'y' или 'z'. Все элементы находятся в плоскости, проходящей через источник и ортогональной оси, заданной в этом свойстве. Для примера, когда ArrayNormal для свойства задано значение 'x'элементы массива находятся в yz -плоскости, как показано на рисунке. Рисунок показывает элемент URA 2 на 4 с элементами, разнесенными на d метра в y и z направлениях.
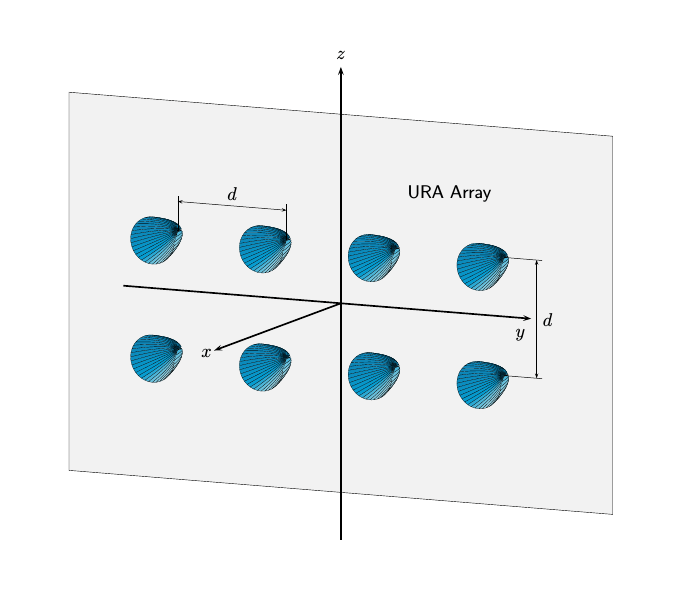
Направление борсайта элемента. В URA, как и ULA, направления boresight каждого элемента указывают в одном направлении. Вы управляете этим направлением, используя ArrayNormal свойство. Для URA, показанного на предыдущем рисунке, ArrayNormal для свойства задано значение 'x'. Затем элемент boresight указывает вдоль оси x .
| Значение свойства ArrayNormal | Положения элемента и направления борсайта |
|---|---|
'x' | Элементы массива лежат на yz -плане. Векторы boresight элемента указывают вдоль оси x. |
'y' | Элементы массива лежат на zx -плане. Векторы boresight элемента указывают вдоль оси y. |
'z' | Элементы массива лежат на xy -плане. Векторы boresight элемента указывают вдоль оси z. |
Локальные координаты, адаптированные к равномерному прямоугольному массиву
Создайте два примера равномерных прямоугольных массивов и отобразите координаты элементов относительно локальных систем координат, заданных массивами.
Сначала создайте URA 2 на 4 с интервалом полуметровых элементов.
sURA = phased.URA('Size',[2 4],'ElementSpacing',[0.5 0.5]); ElementLocs = getElementPosition(sURA)
ElementLocs = 3×8
0 0 0 0 0 0 0 0
-0.7500 -0.7500 -0.2500 -0.2500 0.2500 0.2500 0.7500 0.7500
0.2500 -0.2500 0.2500 -0.2500 0.2500 -0.2500 0.2500 -0.2500
viewArray(sURA)

Центр фазы массива является средним значением положений элемента массива. Источник системы координат массива устанавливается в центр фазы массива.
disp(mean(ElementLocs'))
0 0 0
Поскольку массив имеет четное количество элементов в каждой строке и столбце, ни один элемент массива фактически не находится в центре фазы (0,0,0).
Затем создайте URA 5 на 3 с тридцатисантиметровым элементом интервалом.
sURA1 = phased.URA([5 3],'ElementSpacing',[0.3 0.3]);
ElementLocs = getElementPosition(sURA1)ElementLocs = 3×15
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
-0.3000 -0.3000 -0.3000 -0.3000 -0.3000 0 0 0 0 0 0.3000 0.3000 0.3000 0.3000 0.3000
0.6000 0.3000 0 -0.3000 -0.6000 0.6000 0.3000 0 -0.3000 -0.6000 0.6000 0.3000 0 -0.3000 -0.6000
viewArray(sURA1)

Поскольку массив имеет нечетное количество элементов в каждой строке и столбце, центральный элемент массива находится в центре фазы.
Сигнал приходит в массив из точки в 1000 метрах вдоль оси + X глобальной системы координат. Локальный массив URA повернута на 30 степени по часовой стрелке вокруг оси Y. Вычислите угол прихода сигнала в осях локального массива.
laxes = roty(30); [rng,ang] = rangeangle([1000,0,0]',[0,0,0]',laxes)
rng = 1.0000e+03
ang = 2×1
0
30.0000
Источник массива и центр фазы. Равномерный круговой массив (UCA) является массивом антенных или микрофонных элементов, разнесенных под равными углами вокруг круга. The phased.UCA Системный объект создает особый случай UCA. В этом случае направления boresight элемента указывают от источника массива так же, как спицы колеса. Источником локальной системы координат является геометрический центр массива. Геометрия UCA и расположение и ориентация его элементов определяются тремя параметрами: радиусом массива, количеством элементов и ArrayNormal свойство. Элементы автоматически назначаются положения в локальной системе координат. Положения определяются ArrayNormal свойство, которое может принимать значения 'x', 'y' или 'z'. Все элементы находятся в плоскости, проходящей через источник и ортогональной оси, заданной в этом свойстве. Центр фазы массива совпадает с центром геометрии. Для примера, когда ArrayNormal для свойства задано значение 'x'элементы массива находятся в yz -плоскости, как показано на рисунке. Вы можете создать более общий UCA с произвольными направлениями boresight с помощью phased.ConformalArray Системный объект.
Этот рисунок показывает UCA с 8 элементами, лежащими в плоскости yz.
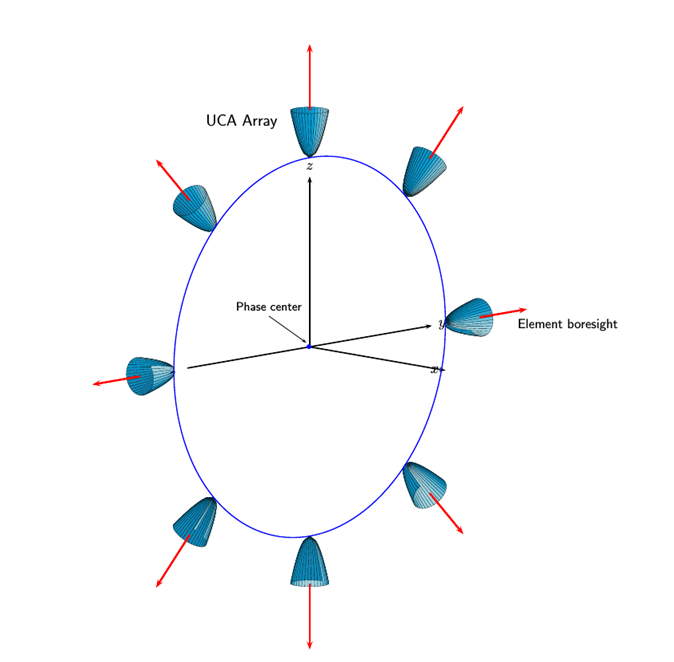
Направления Boresight элемента. В UCA, заданной как phased.UCA Системный объект, направления boresight элемента указывают радиально наружу от источника массива. В UCA, показанном на предыдущем рисунке, потому что ArrayNormal для свойства задано значение 'x'направления боресайта элемента указывают радиально наружу в yz -плане.
| Значение свойства ArrayNormal | Положения элемента и направления борсайта |
|---|---|
'x' | Элементы массива лежат на yz -плане. Все векторы boresight элемента находятся в yz-плоскости и указывают радиально-наружу от источника. |
'y' | Элементы массива лежат на zx -плане. Все векторы boresight элемента находятся в zx-плоскости и указывают радиально-наружу от источника. |
'z' | Элементы массива лежат на xy -плане. Все векторы boresight элемента находятся в xy-плоскости и указывают радиально-наружу от источника. |
Источник массива и центр фазы. Можно использовать phased.ConformalArray для создания массивов произвольной формы. В отличие от случая с равномерными массивами, вы должны задать положения элемента явно. Массив N-element требует спецификации N координат 3-D в локальной системе координат массива. Источник конформного массива может быть расположен в любой произвольной точке. Направления boresight элементов массива конформного массива не должны быть параллельными. Азимут и углы возвышения, определяющие направления боризейта, соответствуют локальной системе координат. Центр фазы массива не должен совпадать с геометрическим центром. Те же свойства применяются и к phased.HeterogeneousConformalArray массив.
Этот рисунок показывает положения и ориентации конформного массива с 4 элементами.
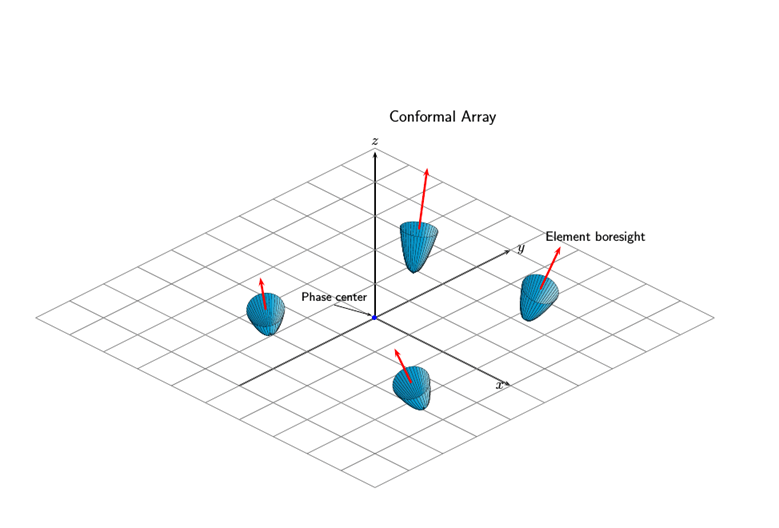
4-Element конформный массив
Создайте массив с 4 элементами с помощью объекта ConformalArray System. Предположим, что рабочая частота составляет 900 МГц. Отобразите геометрию массива и нормальные векторы.
fc = 900e6; c = physconst('LightSpeed'); lam = c/fc; x = [1.0,-.5,0,.8]*lam/2; y = [-.4,-1,.5,1.5]*lam/2; z = [-.3,.3,0.4,0]*lam/2; sIso = phased.CosineAntennaElement(... 'FrequencyRange',[0,1e9]); nv = [-140,-140,90,90;80,80,80,80]; sConformArray = phased.ConformalArray('Element',sIso,... 'ElementPosition',[x;y;z],... 'ElementNormal',nv); pos = getElementPosition(sConformArray)
pos = 3×4
0.1666 -0.0833 0 0.1332
-0.0666 -0.1666 0.0833 0.2498
-0.0500 0.0500 0.0666 0
normvec = getElementNormal(sConformArray)
normvec = 2×4
-140 -140 90 90
80 80 80 80
viewArray(sConformArray,'ShowIndex','All','ShowNormal',true)

Во многих приложениях обработки массивов необходимо преобразовать между глобальными и локальными координатами. Две служебные функции, global2localcoord и local2globalcoord, выполните эти преобразования.
Определите положение цели в прямоугольных координатах в глобальной системе координат. Во-первых, задайте локальные сферические координаты цели относительно URA. Центр URA определяет источник локальной системы координат. Целевое положение в локальных сферических координатах составляет 30 ° азимута, 45 ° повышения и 1000 м области значений. Для преобразования в глобальные прямоугольные координаты задайте положение локальной системы координат источника в глобальных координатах. Источник локальной системы координат находится на расстоянии (1000,500,100) м от глобального источника.
Преобразуйте координаты точки в глобальные прямоугольные координаты. Для преобразования локальных сферических координат в глобальные прямоугольные координаты используйте 'sr' опция в вызове local2globalcoord функция.
gCoord = local2globalcoord([30; 45; 1000],'sr',[1000; 500; 100])gCoord = 3×1
103 ×
1.6124
0.8536
0.8071
Цель расположена на (1612 854 807) м в глобальной системе координат.
Копирайт 2018 The MathWorks, Inc ".
Определите положение цели в локальных сферических координатах с центром в центре фазы массива URA. Центр URA определяет источник локальной системы координат и имеет глобальные прямоугольные координаты (5000,3000,50). Локальными координатными осями URA являются (0,1,0), (1,0,0) и (0,0, -1). Задайте глобальные прямоугольные координаты цели в (1000,500,10).
Преобразуйте координаты цели в локальные сферические прямоугольные координаты. Чтобы преобразовать глобальные прямоугольные координаты в локальные сферические координаты, используйте 'rs' опция в вызове global2localcoord функция.
lCoord = global2localcoord([5000; 3000; 50],'rs',[1000; 500; 100], ... [0 1 0; 1 0 0; 0 0 -1])
lCoord = 3×1
103 ×
0.0580
0.0006
4.7173
Выход имеет форму (az, el, rng). Цель расположена в локальных сферических координатах на отметке 58 ° азимута, 0,6 ° повышения и 4717 м.