Pipe (TL)

Закрытый трубопровод для транспортировки жидкости между компонентами тепловой жидкости

Библиотека:
Simscape/Жидкости/Тепловая жидкость/Трубы и подборы кривой

Описание

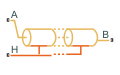
Блок Pipe (TL) моделирует поток тепловой жидкости через трубопровод. Температура через трубу вычисляется из перепада температур между портами, повышением трубопровода и любой дополнительной теплопередачей в порту H.

Трубопровод может иметь постоянную или изменяющееся повышение между портами A и B. Для постоянного дифференциала по повышению используйте параметр Elevation gain from port A to port B. Можно задать повышение переменной, задав для Elevation gain specification значение Variable. Это открывает порт EL физического сигнала.

Вы можете опционально смоделировать гидродинамическую сжимаемость, инерцию и гибкость стенки. Когда эти явления моделируются, свойства потока вычисляются для каждого заданного количества сегментов трубопровода.

Гибкость трубопровода

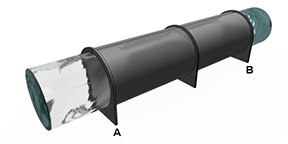
Гибкие стенки моделируются равномерным радиальным расширением, которое сохраняет исходную форму поперечного сечения трубопровода. Можно задать площадь трубопровода в параметре Nominal cross-sectional area, что означает отсутствие заданной геометрии поперечного сечения, смоделированной блоком. Однако блок использует гидравлический диаметр трубопровода в расчетах теплопередачи и падения давления.

Деформация диаметра трубопровода вычисляется как:

$\dot{D} = \frac{D_{S} - D}{τ},$

где:

_DS - постдеформационный, установившийся диаметр трубопровода,

$D_{S} = D_{N} + K_{c} (p - p_{a t m}),$
где K c - Static pressure-diameter compliance, p - давление в трубе, а _patm - атмосферное давление. Принимая упругую деформацию тонкостенной трубы с открытым концом, можно вычислить _K c как:

$K_{c} = \frac{D^{2}}{2 t E},$
где t - толщина стенки трубопровода, а E - модуль Янга.
_DN - номинальный диаметр трубопровода или диаметр, предшествующий деформации:

$D_{N} = \sqrt{\frac{4 S}{π}},$
где S - Nominal cross-sectional area трубопровода.
D - Hydraulic diameter трубопровода.
τ является Viscoelastic pressure time constant.

Теплопередача на стенке трубопровода

Можно смоделировать теплопередачу к стенам трубопровода и от них несколькими способами. Существует две аналитические модели: Gnielinski correlation, который моделирует число Нуссельта как функцию чисел Рейнольдса и Прандтля с предопределенными коэффициентами, и Dittus-Boelter correlation - Nusselt = a*Re^b*Pr^c, который моделирует число Нуссельта как функцию от чисел Рейнольдса и Прандтля с пользовательскими коэффициентами.

The Nominal temperature differential vs. nominal mass flow rate, Tabulated data - Colburn factor vs. Reynolds number, и Tabulated data - Nusselt number vs. Reynolds number & Prandtl number являются параметризациями интерполяционной таблицы на основе предоставленных пользователем данных.

Теплопередача между жидкостью и стенкой трубопровода происходит через конвекцию, Q _Conv и проводимость, _{Q Cond}.

Теплопередача от проводимости:

$Q_{Cond} = \frac{k_{I} S_{H}}{D} (T_{H} - T_{Я}),$

где:

D является Hydraulic diameter, если стенки трубопровода являются жесткими и является установившимся диаметром трубопровода, _DS, если стенки трубопровода являются гибкими.
_kI - теплопроводность тепловой жидкости, заданная внутри для каждого сегмента трубопровода.
_SH - площадь поверхности стенки трубопровода.
_TH - температура стенки трубопровода.
_TI - температура жидкости, принятая во внутреннем узле трубопровода.

Теплопередача от конвекции:

$Q_{Conv} = c_{p,Avg} | {\dot{m}}_{Avg} | (T_{H} - T_{In}) [1 - exp (- \frac{h S_{H}}{c_{p,Avg} | {\dot{m}}_{Avg} |})],$

где:

c _{p, Avg} - это среднее удельное тепло жидкости.
$\dot{m}$ _Avg - это средний массовый расход жидкости через трубопровод.
_TIn - температура входного порта жидкости.
h - коэффициент теплопередачи трубопровода.

Коэффициент h теплопередачи:

$h = \frac{Nu k_{Avg}}{D},$

кроме тех случаев, когда параметризация осуществляется Nominal temperature differential vs. nominal mass flow rate, где _kAvg - средняя теплопроводность тепловой жидкости по всему трубопроводу, а Nu - среднее число Нуссельта в трубопроводе.

Аналитические параметризации

Когда Heat transfer parameterization установлено на Gnielinski correlation и поток турбулентен, среднее число Нуссельта вычисляется как:

$Nu = \frac{\frac{f}{8} (Re - 1000) PR}{1 + 12.7 {(\frac{f}{8})}^{1 / 2} ({Pr}^{2/3} - 1)},$

где:

f - средний коэффициент трения Дарси, согласно корреляции Haaland:

$f = {- 1.8 {log}_{10} [\frac{6.9}{Ре} + {(\frac{ϵ_{R}}{3.7 D})}^{1.11}]}^{-2},$
где ε R - Internal surface absolute roughness трубопровода.
Re - число Рейнольдса.
Pr - число Прандтля.

Когда поток ламинарен, число Нуссельта является Nusselt number for laminar flow heat transfer параметром.

Когда Heat transfer parameterization установлено на Dittus-Boelter correlation и поток турбулентен, среднее число Нуссельта вычисляется как:

$Nu = a {Ре}_{}^{b} {PR}_{}^{c},$

где:

a - значение параметра Coefficient a.
b - значение параметра Exponent b.
c - значение параметра Exponent c.

Блок по умолчанию корреляции Диттуса-Болтера:

$Nu = 0.023 {Ре}_{}^{0.8} {PR}_{}^{0.4} .$

Когда поток ламинарен, число Нуссельта является Nusselt number for laminar flow heat transfer параметром.

Параметризация табличными данными

Когда Heat transfer parameterization установлено на Tabulated data - Colburn factor vs. Reynolds number, среднее число Нуссельта вычисляется как:

$Nu = J_{M} (Ре) {RePr}_{}^{1 / 3} .$

где J M - коэффициент Колборна-Чилтона.

Когда Heat transfer parameterization установлено на Tabulated data - Nusselt number vs. Reynolds number & Prandtl numberчисло Нуссельта интерполировано из трехмерного массива числа Авергэ Нуссельта как функции от среднего числа Рейнольдса и среднего числа Прандтля:

$Nu = Ню (Ре, PR) .$

Когда Heat transfer parameterization установлено на Nominal temperature difference vs. nominal mass flow rate и поток турбулентен, коэффициент теплопередачи вычисляется как:

$h = \frac{h_{N} D_{N}^{1.8}}{{\dot{m}}_{N}^{0.8}} \frac{{\dot{m}}_{В среднем}^{0.8}}{D^{1.8}},$

где:

$\dot{m}$ _N - это Nominal mass flow rate.
$\dot{m}$ _Avg - средний массовый расход жидкости:

${\dot{m}}_{A v g} = \frac{{\dot{m}}_{A} + {\dot{m}}_{B}}{2} .$
h N является номинальным коэффициентом теплопередачи, который вычисляется как :

$h_{N} = \frac{{\dot{m}}_{N} c_{p,N}}{S_{H,N}} ln (\frac{T_{H,N} - T_{In, N}}{T_{H,N} - T_{Out,N}}),$
где:
- _SH,N - номинальная площадь поверхности стенки.
- _TH,N является Nominal wall temperature.
- _TIn,N является Nominal inflow temperature.
- _TOut,N является Nominal outflow temperature.

Эта связь основана на предположении, что число Нуссельта пропорционально числу Рейнольдса:

$\frac{h D}{k} \propto {(\frac{\dot{m} D}{S μ})}^{0.8} .$

Если стенки трубопровода жесткие, выражение коэффициента теплопередачи становится:

$h = \frac{h_{N}}{{\dot{m}}_{N}^{0.8}} {\dot{m}}_{A v g}^{0.8} .$

Падения давления из-за вязкого трения

Существует несколько способов смоделировать перепад давления по трубопроводу. The Haaland correlation предоставляет аналитическую модель для потоков через круглые сечения с коэффициентом трения Дарси. The Nominal pressure drop vs. nominal mass flow rate и Tabulated data - Darcy friction factor vs. Reynolds number параметризации позволяют вам предоставить данные, которые блок будет использовать в качестве интерполяционной таблицы во время симуляции.

Параметризация Analytical

Когда Viscous friction parameterization установлено на Haaland correlation и поток турбулентен, падение давления на трение на стенках трубопровода определяется уравнением Дарси-Вайсбаха:

$p_{A} - p_{I} = f \frac{{\dot{m}}_{A} | {\dot{m}}_{A} |}{2 ρ_{Я} D S^{2}} (\frac{L + L_{Add}}{2}),$

где:

L является Pipe length.
_LE - Aggregate equivalent length of local resistances, которая является эквивалентной длиной трубки, которая вводит такое же количество потерь, как и сумма потерь из-за других локальных сопротивлений в трубке.

Перепад давления между портом B и внутренним узлом I:

$p_{B} - p_{Я} = f \frac{{\dot{m}}_{B} | {\dot{m}}_{B} |}{2 ρ_{Я} D S^{2}} (\frac{L + L_{Add}}{2}),$

Когда поток ламинарен, падение давления на трение вычисляется в терминах Laminar friction constant for Darcy friction factor, λ. Перепад давления между портом A и внутренним узлом I:

$p_{A} - p_{Я} = \frac{λ μ {\dot{m}}_{A}}{2 ρ D^{2} S} (\frac{L + L_{Add}}{2}) .$

Перепад давления между портом B и внутренним узлом I:

$p_{B} - p_{Я} = \frac{λ μ {\dot{m}}_{B}}{2 ρ D^{2} S} (\frac{L + L_{Add}}{2}) .$

Для переходных потоков перепадом давления из-за вязкого трения является сглаженная смесь между значениями для ламинарного и турбулентного падения давления.

Параметризация табличными данными

Когда Viscous friction parameterization установлено на Nominal pressure drop vs. nominal mass flow rate, потеря давления из-за вязкого трения вычисляется по двум половинам трубопровода с коэффициентом потерь _Kp:

$Δ p_{f, A} = \frac{1}{2} K_{p} {\dot{m}}_{A} \sqrt{{\dot{m}}_{A}^{2} + {\dot{m}}_{Th}^{2}}$

$Δ p_{f, B} = \frac{1}{2} K_{p} {\dot{m}}_{B} \sqrt{{\dot{m}}_{B}^{2} + {\dot{m}}_{Th}^{2}}$

где:

${\dot{m}}_{Th}$ является Mass flow rate threshold for flow reversal.
K p - коэффициент падения давления. Для гибких стенок трубопровода коэффициент падения давления равен :

$K_{p} = \frac{p_{N}}{{\dot{m}}_{N}^{2}} D_{N},$
где:
- _pN является Nominal pressure drop.
- $\dot{m}$ _N - это Nominal mass flow rate.
Коэффициент падения давления

$K_{p} = \frac{p_{N}}{{\dot{m}}_{N}^{2}},$
когда стенки трубопровода жесткие. Когда Nominal pressure drop и Nominal mass flow rate параметры являются векторами, значение _Kp определяется как аппроксимация векторных элементов методом наименьших квадратов.

Когда

Когда Viscous friction parameterization установлено на Tabulated data – Darcy friction factor vs. Reynolds numberкоэффициент трения интерполируется из табличных данных как функция от числа Рейнольдса:

$f = f (Re) .$

Баланс импульса

Перепад давления по трубопроводу обусловлен давлением в портах трубопровода, трением на стенках трубопровода и гидростатическими изменениями из-за любой разницы в вертикальном положении:

$p_{A} - p_{B} = Δ p_{f} + ρ_{Я} g Δ z,$

где:

_pA - давление в порте A.
_pB - давление в порте B.
_Δpf - перепад давления из-за вязкого трения, _{Δpf,A+Δpf,B}.
g Gravitational acceleration.
Δz перепад повышений между портом A и портом B или _{zA - zB}.
_ρI - внутренняя плотность жидкости, которая измеряется на каждом сегменте трубопровода. Если динамическая сжимаемость жидкости не моделируется, это:

$p_{I} = \frac{p_{A} + p_{B}}{2} .$

Когда инерция жидкости не моделируется, баланс импульса между портом A и внутренним узлом I:

$p_{A} - p_{Я} = Δ p_{f, A} + ρ_{Я} g \frac{Δ z}{2} .$

Когда инерция жидкости не моделируется, баланс импульса между портом B и внутренним узлом I:

$p_{B} - p_{Я} = Δ p_{f, B} - ρ_{Я} g \frac{Δ z}{2} .$

Когда моделируется инерция жидкости, баланс импульса между портом A и внутренним узлом I:

$p_{A} - p_{Я} = Δ p_{f, A} + ρ_{Я} g \frac{Δ z}{2} + \frac{{\ddot{m}}_{A}}{S} \frac{L}{2},$

где:

$\ddot{m}$ _A - инерция жидкости в порту A.
L является Pipe length.
S является Nominal cross-sectional area.

Когда моделируется инерция жидкости, баланс импульса между портом B и внутренним узлом I:

$p_{B} - p_{Я} = Δ p_{f, B} - ρ_{Я} g \frac{Δ z}{2} + \frac{{\ddot{m}}_{B}}{S} \frac{L}{2},$

где

$\ddot{m}$ _B - инерция жидкости в порту B.

Дискретизация трубопровода

Можно разделить трубопровод на несколько сегментов. Если у трубопровода больше одного сегмента, для каждого сегмента вычисляются массовый расход, энергетический поток и уравнения баланса импульса. Наличие нескольких сегментов трубопровода может позволить вам отслеживать изменения к переменным, таким как плотность жидкости, когда моделируется динамическая сжимаемость жидкости.

Если вы хотите захватить конкретные явления в вашем приложении, такие как водяной молоток, выберите ряд сегментов, которые обеспечивают достаточное разрешение переходного процесса. Следующая формула из теоремы Найквиста о дискретизации трубопроводов в минимум N сегментов:

$N = 2 L \frac{f}{c},$

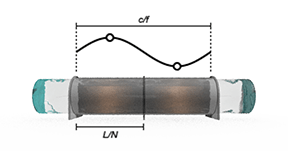
где:

L является Pipe length.
f - переходная частота.
c - скорость звука.

В некоторых случаях, таких как моделирование тепловых переходных процессов вдоль трубопровода, может быть лучше, чтобы ваше приложение соединяло несколько блоков Pipe (TL) последовательно.

Баланс массы

Для жесткой трубы с несжимаемой жидкостью уравнение разговора массы трубопровода является:

${\dot{m}}_{A} + {\dot{m}}_{B} = 0,$

где:

$\dot{m}$ _A - массовый расход жидкости в порту A.
$\dot{m}$ _B - массовый расход жидкости в порту B.

Для гибкого трубопровода с несжимаемой жидкостью уравнение сохранения массы трубопровода является:

${\dot{m}}_{A} + {\dot{m}}_{B} = ρ_{Я} \dot{V},$

где:

_ρI - плотность тепловой жидкости во внутреннем узле I. Каждый сегмент трубопровода имеет внутренний узел.
$\dot{V}$ - скорость деформации объема трубопровода.

Для гибкого трубопровода с сжимаемой жидкостью уравнение сохранения массы трубопровода является: Эта зависимость получена модулем объемной упругости расширения и коэффициентом теплового расширения тепловой жидкости:

${\dot{m}}_{A} + {\dot{m}}_{B} = ρ_{Я} \dot{V} + ρ_{Я} V (\frac{{\dot{p}}_{Я}}{β_{I}} - α_{Я} {\dot{T}}_{Я}),$

где:

_pI - давление тепловой жидкости во внутреннем узле I.
$\dot{T}$ _I - скорость изменения температуры тепловой жидкости во внутреннем узле I.
_βI - тепловая жидкость модуля объемной упругости.
α - коэффициент теплового расширения жидкости.

Энергетический баланс

Скорость накопления энергии в трубопроводе во внутреннем узле I определяется как:

$\dot{E} = ϕ_{A} + ϕ_{B} + ϕ_{H} - {\dot{m}}_{A v g} g Δ z,$

где:

_ϕA - энергетическая скорость потока жидкости в порту A.
_ϕB - энергетическая скорость потока жидкости в порту B.
_ϕH - энергетическая скорость потока жидкости в порту H.

Общая энергия определяется как:

$E = ρ_{I} u_{Я} V,$

где:

_uI - специфическая для жидкости внутренняя энергия в узле I.
V - объем трубопровода.

Если жидкость сжимаема, выражение для скорости накопления энергии является:

$\dot{E} = ρ_{Я} V {(\frac{d u}{d p} \frac{d p}{d t} + \frac{d u}{d T} \frac{d T}{d t})}_{Я} .$

Если жидкость сжимаема, а стенки трубопровода гибки, выражение для скорости накопления энергии является:

$\dot{E} = ρ_{Я} V {(\frac{d u}{d p} \frac{d p}{d t} + \frac{d u}{d T} \frac{d T}{d t})}_{Я} + (ρ_{I} u_{Я} + p_{Я}) {(\frac{d V}{d t})}_{Я} .$

Порты

Вход

расширить все

`EL` - различие повышений портов
физический сигнал

Переменный дифференциал повышения между портом A и B, заданный как физический сигнал.

Сохранение

расширить все

`A` - Открытие трубопровода
тепловая жидкость

Порт входа или выхода жидкости в трубопровод.

`B` - Открытие трубопровода
тепловая жидкость

Порт входа или выхода жидкости в трубопровод.

`H` - Стенки трубопровода
тепловой

Температура стенки трубопровода.

Параметры

расширить все

Строение

`Fluid dynamic compressibility` - Моделировать ли динамическую сжимаемость жидкости
`On` (по умолчанию) | `Off`

Моделирует ли какое-либо изменение плотности жидкости из-за сжимаемости жидкости. Когда Fluid compressibility установлено на On, изменения из-за массового расхода жидкости в блок вычисляются в дополнение к изменениям плотности из-за изменений давления.

`Fluid inertia` - Моделировать ли ускорение жидкости
`On` (по умолчанию) | `Off`

Будет ли учитываться ускорение массового расхода жидкости из-за массы жидкости.

Зависимости

Чтобы включить этот параметр, установите Fluid dynamic compressibility равным On.

`Number of segments` - Дискретизация трубопровода
`1` (по умолчанию) | положительный безюнитный скаляр

Количество делений трубопровода. Каждое деление представляет отдельный сегмент, над которым вычисляется давление, в зависимости от давления на входе в трубопровод, сжимаемости жидкости и гибкости стенки, если применимо. Объем жидкости в каждом сегменте остается фиксированным.

Зависимости

Чтобы включить этот параметр, установите Fluid dynamic compressibility равным On.

`Pipe total length` - Общая длина трубопровода
`5 m` (по умолчанию) | положительная скалярная величина в единицах измерения длины

Общая длина трубопровода по всем сегментам трубопровода.

`Nominal cross-sectional area` - Площадь трубопровода поперечного сечения без деформации
`0.01` m ^ 2 (по умолчанию) | положительная скалярная величина в единицах площади

Площадь поперечного сечения трубопровода без деформаций.

`Pipe wall specification` - Задает гибкость стенки
`Rigid` (по умолчанию) | `Flexible`

Задает стенки трубопровода как жесткие или гибкие. Гибкие стенки моделируются равномерным радиальным расширением, которое сохраняет исходную форму поперечного сечения трубопровода.

Зависимости

Чтобы включить этот параметр, установите Fluid dynamic compressibility равным On.

`Hydraulic diameter` - Эффективный диаметр некруглых сечений
`0.1128 m` (по умолчанию) | положительная скалярная величина в единицах измерения длины

Эффективный диаметр, используемый в теплопередаче, балансе импульса и уравнениях гибкости трубопровода. Для некруглых сечений гидравлический диаметр является эффективным диаметром жидкости в трубопроводе. Для круглых сечений гидравлический диаметр и диаметр трубопровода совпадают.

Зависимости

Чтобы включить этот параметр, установите либо:

Fluid dynamic compressibility с Off.
Pipe wall specification с Rigid и Fluid dynamic compressibility к On.

`Elevation gain specification` - Задать свойство повышения трубопровода
`Constant` (по умолчанию) | `Variable`

Установите повышение трубопровода равной либо Constant или Variable. Выбор Variable отображает порт EL физического сигнала.

`Elevation gain from port A to port B` - Разница в вертикальном положении порта A на порт B
`0 m` (по умолчанию) | положительная скалярная величина в единицах измерения длины

Перепад повышений для трубопроводов постоянной высоты. Коэффициент усиления повышения должен быть меньше или равен общей длине трубопровода.

Зависимости

Чтобы включить этот параметр, установите Elevation gain specification равным Constant.

`Gravitational acceleration` - Ускорение от силы тяжести на среднем повышении трубопровода
`9.81 m/s^2` (по умолчанию) | положительная скалярная величина в единицах измерения длины/времени ^

Константа ускорения свободного падения (g) на среднем повышении трубопровода.

`Static pressure-diameter compliance` - Мера деформации трубопровода
`1.2e-6 m/MPa` (по умолчанию) | положительная скалярная величина в единицах измерения длины/давления

Коэффициент радиальной деформации трубопровода от изменения давления. Это свойство материала трубопровода.

Зависимости

Чтобы включить этот параметр, установите Pipe wall specification равным Flexible.

`Viscoelastic process time constant` - Время деформации трубопровода константа
`0.01 s` (по умолчанию) | положительная скалярная величина в единицах времени

Время, необходимое для достижения стенкой устойчивого состояния после деформации трубопровода. Этот параметр влияет на динамическое изменение объема трубопровода.

Зависимости

Чтобы включить этот параметр, установите Pipe wall specification равным Flexible.

Вязкое трение

`Viscous friction parameterization` - Модель трения
`Haaland correlation` (по умолчанию) | `Nominal pressure drop vs. nominal mass flow rate` | `Tabulated data - Darcy friction factor vs. Reynolds number`

Параметризация падения давления из-за трения стенки. Доступны как аналитические, так и табличные составы.

`Aggregate equivalent length of local resistances` - Незначительное падения давления в трубопроводе в виде длины
`1 m` (по умолчанию) | положительная скалярная величина в единицах измерения длины

Длина трубопровода, которая могла бы привести к эквивалентным гидравлическим потерям, как и трубы с поворотами, изменениями площади или другими неоднородностями. Эффективная длина трубопровода является суммой длины трубопровода и совокупной эквивалентной длины локальных сопротивлений.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization равным Haaland correlation.

`Internal surface absolute roughness` - Абсолютная шероховатость стенки трубопровода
`1.5e-5 m` (по умолчанию) | положительная скалярная величина в единицах измерения длины

Абсолютная шероховатость стенки трубопровода. Этот параметр используется для определения коэффициента трения Дарси, который способствует падению давления в трубопроводе.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization равным Haaland correlation.

`Shape factor for laminar flow viscous friction` - Коэффициент трения для ламинарных течений
`64` (по умолчанию) | положительный безюнитный скаляр

Коэффициент трения для ламинарных течений. Коэффициент трения Дарси фиксирует вклад трения стенки в вычислениях падения давления.

`Laminar flow upper Reynolds number limit` - число Рейнольдса, ниже которого поток ламинарен
`2e+3` (по умолчанию) | положительный безюнитный скаляр

Число Рейнольдса, ниже которого поток ламинарен. Выше этого порога поток переходит к турбулентному, достигнув турбулентного режима при Turbulent flow lower Reynolds number limit настройке.

`Turbulent flow lower Reynolds number limit` - число Рейнольдса, выше которого поток турбулентен
`4e+3` (по умолчанию) | положительный безюнитный скаляр

Число Рейнольдса, выше которого поток турбулентен. Ниже этого порога поток постепенно переходит к ламинарному, достигнув ламинарного режима при Laminar flow upper Reynolds number limit настройке.

`Nominal mass flow rate` - Массовый расход жидкости из трубопровода
`[0.1 1] kg/s` (по умолчанию) | скаляр или вектор чисел в единицах измерения массы/времени

Номинальный массовый расход жидкости трубопровода, используемая для вычисления коэффициента падения давления, заданного в виде скаляра или вектора. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Nominal pressure drop. Когда этот параметр передается как вектор, скалярное значение Kp определяется как аппроксимация векторных элементов методом наименьших квадратов.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization равным Nominal pressure drop vs. nominal mass flow rate.

`Nominal pressure drop` - Перепад давления по трубопроводу
`[0.001 0.01] MPa` (по умолчанию) | скаляр или вектор чисел в единицах измерения давления

Номинальный перепад давления в трубопроводе для вычисления коэффициента падения давления в виде скаляра или вектора. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальный массовый расход жидкости. Когда этот параметр передается как вектор, скалярное значение Kp определяется как аппроксимация векторных элементов методом наименьших квадратов.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization равным Nominal pressure drop vs. nominal mass flow rate.

`Mass flow rate threshold for flow reversal` - Порог, ниже которого применяется численное сглаживание
`1e-6 kg/s` (по умолчанию) | положительная скалярная величина в единицах измерения массы/времени

Массовый расход жидкости порог для обратного потока. Переходная область определяется около 0 кг/с между положительными и отрицательными значениями порога массового расхода жидкости. В пределах этой переходной области к отклику потока применяется численное сглаживание. Пороговое значение должно быть больше 0.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization равным Nominal pressure drop vs. nominal mass flow rate.

`Reynolds number vector for turbulent Darcy friction factor` - числа Рейнольдса, при которых можно свести в таблицу коэффициент трения Дарси
`[ 400 1000 1.5e+3 3e+3 4e+3 6e+3 1e+4 2e+4 4e+4 6e+4 1e+5 1e+8 ]` (по умолчанию) | вектор положительных бесчисленных чисел

Вектор чисел Рейнольдса для табличной параметризации коэффициента трения Дарси. Векторные элементы образуют независимую ось с параметром вектора коэффициента трения Дарси. Векторные элементы должны быть перечислены в порядке возрастания и должны быть больше 0. Для обратных потоков или потоков от B до A те же данные применяются в противоположном направлении.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization равным Tabulated data - Darcy friction factor vs. Reynolds number.

`Darcy friction factor vector` - коэффициент трения Дарси при табличных числах Рейнольдса
`[ 0.264 0.112 0.07099999999999999 0.0417 0.0387 0.0268 0.025 0.0232 0.0226 0.022 0.0214 0.0214 ]` (по умолчанию) | вектор положительных бесчисленных чисел

Вектор Дарси коэффициентов трения для табличной параметризации коэффициента трения Дарси. Векторные элементы должны совпадать один к одному с элементами вектора числа Рейнольдса для турбулентного параметра коэффициента трения Дарси, и должны быть уникальными и большими или равными 0.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization равным Tabulated data - Darcy friction factor vs. Reynolds number.

Теплопередача

`Heat transfer parameterization` - Метод, которым можно захватить конвективную теплопередачу со стенкой трубопровода
`Gnielinski correlationNominal temperature differential vs. nominal mass flow rate` (по умолчанию) | `Dittus-Boelter correlation` | `Tabulated data - Colburn factor vs. Reynolds number` | `Tabulated data - Nusselt number vs. Reynolds number & Prandtl number`

Метод вычисления коэффициента теплопередачи между жидкостью и стенкой трубопровода. Доступны аналитические и табличные данные параметризации.

`Nusselt number for laminar flow heat transfer` - число Нуссельта для использования в расчетах теплопередачи для ламинарных течений
`3.66` (по умолчанию)

Отношение конвективного к проводящему теплопередаче в ламинарном режиме течения жидкости. Число Нуссельта жидкости влияет на скорость теплопередачи.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization либо на:

Gnielinski correlation.
Nominal temperature differential vs. nominal mass flow rate.
Dittus-Boelter correlation.

`Nominal mass flow rate` - Массовый расход жидкости из трубопровода
`[0.1 1] kg/s` (по умолчанию) | скаляр или вектор чисел в единицах измерения массы/времени

Номинальный массовый расход жидкости трубопровода, используемая для вычисления коэффициента теплопередачи, заданного в виде скаляра или вектора. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальная температура притока. Когда этот параметр передается как вектор, скалярное значение h p определяется как аппроксимация векторных элементов методом наименьших квадратов.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization равным Nominal temperature differential vs. nominal mass flow rate.

`Nominal inflow temperature` - Температура входного отверстия трубопровода
`[293.15 293.15] K` (по умолчанию) | скаляр или вектор чисел в единицах измерения температуры

Номинальная температура на входе жидкости, используемая для вычисления коэффициента теплопередачи, заданного как скаляр или вектор. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальный массовый расход жидкости. Когда этот параметр задается как вектор, h скалярного значения определяется как аппроксимация векторных элементов методом наименьших квадратов.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization равным Nominal temperature differential vs. nominal mass flow rate.

`Nominal outflow temperature` - Температура на выходе трубопровода
`[300 300] K`'(по умолчанию) | скаляр или вектор чисел в единицах измерения температуры

Номинальная температура на выходе жидкости, используемая для вычисления коэффициента теплопередачи, заданного как скаляр или вектор. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальный массовый расход жидкости. Когда этот параметр задается как вектор, h скалярного значения определяется как аппроксимация векторных элементов методом наименьших квадратов.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization равным Nominal temperature differential vs. nominal mass flow rate.

`Nominal inflow pressure` - Давление на входе в трубопровод
`[0.101325 0.101325] MPa` (по умолчанию) | скаляр или вектор чисел в единицах измерения давления

Номинальное давление на входе жидкости, используемое для вычисления коэффициента теплопередачи, заданного как скаляр или вектор. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальный массовый расход жидкости. Когда этот параметр задается как вектор, h скалярного значения определяется как аппроксимация векторных элементов методом наименьших квадратов.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization равным Nominal temperature differential vs. nominal mass flow rate.

`Nominal wall temperature` - Температура стенки трубопровода
`[303.15 303.15] K` (по умолчанию) | скаляр или вектор чисел в единицах измерения температуры

Температура стенки трубопровода, используемая для вычисления коэффициента теплопередачи, заданного как скаляр или вектор. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальный массовый расход жидкости. Когда этот параметр задается как вектор, h скалярного значения определяется как аппроксимация векторных элементов методом наименьших квадратов.

Зависимости

Чтобы включить эту температуру, установите Heat transfer parameterization равным Nominal temperature differential vs. nominal mass flow rate.

`Coefficient a` - Эмпирическая постоянная a корреляции Диттуса-Болтера
`0.023` (по умолчанию) | положительный безюнитный скаляр

Эмпирические постоянные a для использования в корреляции Диттуса-Болтера. Корреляция связывает число Нуссельта в турбулентных потоках с коэффициентом теплопередачи.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization равным Dittus-Boelter correlation.

`Exponent b` - Эмпирическая постоянная b корреляции Диттуса-Болтера
`0.8` (по умолчанию) | положительный безюнитный скаляр

Эмпирические постоянные b для использования в корреляции Диттуса-Болтера. Корреляция связывает число Нуссельта в турбулентных потоках с коэффициентом теплопередачи.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization равным Dittus-Boelter correlation.

`Exponent c` - Эмпирическая постоянная c корреляции Диттуса-Болтера
`0.4` (по умолчанию) | положительный безюнитный скаляр

Эмпирические постоянные c для использования в корреляции Диттуса-Болтера. Корреляция связывает число Нуссельта в турбулентных потоках с коэффициентом теплопередачи. Значение по умолчанию отражает теплопередачу жидкости.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization равным Dittus-Boelter correlation.

`Reynolds number vector for Colburn factor` - числа Рейнольдса, при которых можно свести в таблицу коэффициент Колборна
`[100 150 1000]` (по умолчанию) | вектор положительных бесчисленных чисел

Вектор чисел Рейнольдса для табличной параметризации коэффициента Колборна. Векторные элементы образуют независимую ось с параметром вектора коэффициента Колборна. Векторные элементы должны быть перечислены в порядке возрастания и должны быть больше 0. Этот параметр должен иметь то же количество элементов, что и вектор коэффициента Колборна. Для обратных потоков или потоков от B до A те же данные применяются в противоположном направлении.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization равным Tabulated data - Colburn factor vs. Reynolds number.

`Colburn factor vector` - Коэффициенты Колбёрна, при которых табличные числа Рейнольдса
`[0.019 0.013 0.002]` (по умолчанию) | вектор положительных бесчисленных чисел

Вектор коэффициентов Кольбруна для табличной параметризации коэффициента Колборна. Векторные элементы образуют независимую ось с вектором числа Рейнольдса для параметра коэффициента Колборна. Этот параметр должен иметь то же количество элементов, что и вектор числа Рейнольдса для коэффициента Колборна.

Зависимости

Этот параметр активен, когда Heat transfer parameterization параметров блоков установлено на Tabulated data - Colburn factor vs. Reynolds number.

`Reynolds number vector for Nusselt number` - число Рейнольдса, при котором можно свести в таблицу число Нуссельта
`[100 150 100]` (по умолчанию) | вектор положительных бесчисленных чисел

Вектор чисел Рейнольдса для табличной параметризации числа Нуссельта. Этот вектор образует независимую ось с параметром Prandtl number vector for Nusselt number для 2-D зависимых Nusselt number table. Векторные элементы должны быть перечислены в порядке возрастания и должны быть больше 0.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization равным Tabulated data - Nusselt number vs. Reynolds number & Prandtl number.

`Prandtl number vector for Nusselt number` - числа Прандтля, при которых можно свести в таблицу число Нуссельта
`[1 10]` (по умолчанию) | вектор положительных бесчисленных чисел

Вектор чисел Прандтля для табличной параметризации числа Нуссельта. Этот вектор образует независимую ось с параметром Reynolds number vector for Nusselt number для 2-D зависимых Nusselt number table. Векторные элементы должны быть перечислены в порядке возрастания.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization равным Tabulated data - Nusselt number vs. Reynolds number & Prandtl number.

`Nusselt number table` - числа Нуссельта по табличным числам Рейнольдса и Прандтля
`[ 3.72 4.21; 3.75 4.44; 4.21 7.15 ]` (по умолчанию) | матрица положительных бесчисленных чисел

M -by - N матрица чисел Нуссельта при заданных числах Рейнольдса и Прандтля. Линейная интерполяция используется между элементами таблицы. M и N являются размерами соответствующих векторов:

M - количество векторных элементов в параметре Reynolds number vector for Nusselt number.
N - количество векторных элементов в параметре Prandtl number vector for Nusselt number.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization равным Tabulated data - Nusselt number vs. Reynolds number & Prandtl number.

Начальные условия

`Initial liquid temperature` - Абсолютная температура в трубопроводе в начале симуляции
`293.15 K` (по умолчанию) | положительная скалярная величина или вектор в единицах измерения температуры

Температура жидкости в начале симуляции, заданная как скаляр или вектор. Вектор n элементов long определяет температуру жидкости для каждого из n сегментов трубопровода. Если вектор имеет длину два элемента, температура вдоль трубопровода линейно распределена между двумя значениями элемента. Если вектор имеет длину три или более элемента, начальная температура в n-м сегменте задается n-м элементом вектора.

`Initial liquid pressure` - Абсолютное давление в трубопроводе в начале симуляции
`0.101325 MPa` (по умолчанию) | положительная скалярная величина или вектор в единицах измерения давления

Абсолютное давление жидкости в начале симуляции, заданное как скаляр или вектор. Вектор n элементов задает давление жидкости для каждого из n сегментов трубопровода. Если вектор имеет длину в два элемента, давление вдоль трубопровода линейно распределяется между двумя значениями элемента. Если вектор имеет длину три или более элемента, начальное давление в n-м сегменте устанавливается n-м элементом вектора.

Примеры моделей

Система отопления зданий

Моделируйте простую систему отопления дома. Модель содержит нагреватель, контроллер и конструкцию дома с четырьмя излучателями и четырьмя комнатами. Каждая комната обменивается теплом с окружением через наружные стенки, крышу и окна. Каждый путь моделируется как комбинация тепловой конвекции, тепловой проводимости и тепловой массы. Принято, что тепло не передается внутренне между помещениями. Нагреватель состоит из печи, бойлера, аккумулятора и насоса для циркуляции горячей воды в системе. Контроллер начинает подачу топлива в печь, если общая средняя температура помещений падает ниже 21 степени C, и он останавливается, если температура превышает 25 степени C. Симуляция рассчитывает стоимость нагрева и температуру в помещении.

Электрическое Транспортное средство Тепловое Управление

Моделирует систему теплового управления электрического транспортного средства аккумулятора. Система состоит из двух циклов теплоносителя, холодильного цикла и кабины ОВКВ цикла. Тепловой нагрузкой являются батареи, силовой агрегат и кабина.

Документация

Pipe (TL)

Описание

Гибкость трубопровода

Теплопередача на стенке трубопровода

Падения давления из-за вязкого трения

Баланс импульса

Дискретизация трубопровода

Баланс массы

Энергетический баланс

Порты

Вход

EL - различие повышений портов физический сигнал

Сохранение

A - Открытие трубопровода тепловая жидкость

B - Открытие трубопровода тепловая жидкость

H - Стенки трубопровода тепловой

Параметры

Fluid dynamic compressibility - Моделировать ли динамическую сжимаемость жидкости On (по умолчанию) | Off

Fluid inertia - Моделировать ли ускорение жидкости On (по умолчанию) | Off

Зависимости

Number of segments - Дискретизация трубопровода 1 (по умолчанию) | положительный безюнитный скаляр

Зависимости

Pipe total length - Общая длина трубопровода 5 m (по умолчанию) | положительная скалярная величина в единицах измерения длины

Nominal cross-sectional area - Площадь трубопровода поперечного сечения без деформации 0.01 m ^ 2 (по умолчанию) | положительная скалярная величина в единицах площади

Pipe wall specification - Задает гибкость стенки Rigid (по умолчанию) | Flexible

Зависимости

Hydraulic diameter - Эффективный диаметр некруглых сечений 0.1128 m (по умолчанию) | положительная скалярная величина в единицах измерения длины

Зависимости

Elevation gain specification - Задать свойство повышения трубопровода Constant (по умолчанию) | Variable

Elevation gain from port A to port B - Разница в вертикальном положении порта A на порт B 0 m (по умолчанию) | положительная скалярная величина в единицах измерения длины

Зависимости

Static pressure-diameter compliance - Мера деформации трубопровода 1.2e-6 m/MPa (по умолчанию) | положительная скалярная величина в единицах измерения длины/давления

Зависимости

Viscoelastic process time constant - Время деформации трубопровода константа 0.01 s (по умолчанию) | положительная скалярная величина в единицах времени

Зависимости

Viscous friction parameterization - Модель трения Haaland correlation (по умолчанию) | Nominal pressure drop vs. nominal mass flow rate | Tabulated data - Darcy friction factor vs. Reynolds number

Зависимости

Internal surface absolute roughness - Абсолютная шероховатость стенки трубопровода 1.5e-5 m (по умолчанию) | положительная скалярная величина в единицах измерения длины

Зависимости

Shape factor for laminar flow viscous friction - Коэффициент трения для ламинарных течений 64 (по умолчанию) | положительный безюнитный скаляр

Laminar flow upper Reynolds number limit - число Рейнольдса, ниже которого поток ламинарен 2e+3 (по умолчанию) | положительный безюнитный скаляр

Turbulent flow lower Reynolds number limit - число Рейнольдса, выше которого поток турбулентен 4e+3 (по умолчанию) | положительный безюнитный скаляр

Nominal mass flow rate - Массовый расход жидкости из трубопровода [0.1 1] kg/s (по умолчанию) | скаляр или вектор чисел в единицах измерения массы/времени

Зависимости

Nominal pressure drop - Перепад давления по трубопроводу [0.001 0.01] MPa (по умолчанию) | скаляр или вектор чисел в единицах измерения давления

Зависимости

Зависимости

Зависимости

Зависимости

Nusselt number for laminar flow heat transfer - число Нуссельта для использования в расчетах теплопередачи для ламинарных течений 3.66 (по умолчанию)

Зависимости

Nominal mass flow rate - Массовый расход жидкости из трубопровода [0.1 1] kg/s (по умолчанию) | скаляр или вектор чисел в единицах измерения массы/времени

Зависимости

Nominal inflow temperature - Температура входного отверстия трубопровода [293.15 293.15] K (по умолчанию) | скаляр или вектор чисел в единицах измерения температуры

Зависимости

Nominal outflow temperature - Температура на выходе трубопровода [300 300] K'(по умолчанию) | скаляр или вектор чисел в единицах измерения температуры

Зависимости

Nominal inflow pressure - Давление на входе в трубопровод [0.101325 0.101325] MPa (по умолчанию) | скаляр или вектор чисел в единицах измерения давления

Зависимости

Nominal wall temperature - Температура стенки трубопровода [303.15 303.15] K (по умолчанию) | скаляр или вектор чисел в единицах измерения температуры

Зависимости

Coefficient a - Эмпирическая постоянная a корреляции Диттуса-Болтера 0.023 (по умолчанию) | положительный безюнитный скаляр

Зависимости

Exponent b - Эмпирическая постоянная b корреляции Диттуса-Болтера 0.8 (по умолчанию) | положительный безюнитный скаляр

Зависимости

Exponent c - Эмпирическая постоянная c корреляции Диттуса-Болтера 0.4 (по умолчанию) | положительный безюнитный скаляр

Зависимости

Reynolds number vector for Colburn factor - числа Рейнольдса, при которых можно свести в таблицу коэффициент Колборна [100 150 1000] (по умолчанию) | вектор положительных бесчисленных чисел

Зависимости

Colburn factor vector - Коэффициенты Колбёрна, при которых табличные числа Рейнольдса [0.019 0.013 0.002] (по умолчанию) | вектор положительных бесчисленных чисел

Зависимости

Reynolds number vector for Nusselt number - число Рейнольдса, при котором можно свести в таблицу число Нуссельта [100 150 100] (по умолчанию) | вектор положительных бесчисленных чисел

Зависимости

Prandtl number vector for Nusselt number - числа Прандтля, при которых можно свести в таблицу число Нуссельта [1 10] (по умолчанию) | вектор положительных бесчисленных чисел

Зависимости

Nusselt number table - числа Нуссельта по табличным числам Рейнольдса и Прандтля [ 3.72 4.21; 3.75 4.44; 4.21 7.15 ] (по умолчанию) | матрица положительных бесчисленных чисел

Зависимости

Примеры моделей

Система отопления зданий

`EL` - различие повышений портов
физический сигнал

`A` - Открытие трубопровода
тепловая жидкость

`B` - Открытие трубопровода
тепловая жидкость

`H` - Стенки трубопровода
тепловой

`Fluid dynamic compressibility` - Моделировать ли динамическую сжимаемость жидкости
`On` (по умолчанию) | `Off`

`Fluid inertia` - Моделировать ли ускорение жидкости
`On` (по умолчанию) | `Off`

`Number of segments` - Дискретизация трубопровода
`1` (по умолчанию) | положительный безюнитный скаляр

`Pipe total length` - Общая длина трубопровода
`5 m` (по умолчанию) | положительная скалярная величина в единицах измерения длины

`Nominal cross-sectional area` - Площадь трубопровода поперечного сечения без деформации
`0.01` m ^ 2 (по умолчанию) | положительная скалярная величина в единицах площади

`Pipe wall specification` - Задает гибкость стенки
`Rigid` (по умолчанию) | `Flexible`

`Hydraulic diameter` - Эффективный диаметр некруглых сечений
`0.1128 m` (по умолчанию) | положительная скалярная величина в единицах измерения длины

`Elevation gain specification` - Задать свойство повышения трубопровода
`Constant` (по умолчанию) | `Variable`

`Elevation gain from port A to port B` - Разница в вертикальном положении порта A на порт B
`0 m` (по умолчанию) | положительная скалярная величина в единицах измерения длины

`Static pressure-diameter compliance` - Мера деформации трубопровода
`1.2e-6 m/MPa` (по умолчанию) | положительная скалярная величина в единицах измерения длины/давления

`Viscoelastic process time constant` - Время деформации трубопровода константа
`0.01 s` (по умолчанию) | положительная скалярная величина в единицах времени

`Viscous friction parameterization` - Модель трения
`Haaland correlation` (по умолчанию) | `Nominal pressure drop vs. nominal mass flow rate` | `Tabulated data - Darcy friction factor vs. Reynolds number`

`Internal surface absolute roughness` - Абсолютная шероховатость стенки трубопровода
`1.5e-5 m` (по умолчанию) | положительная скалярная величина в единицах измерения длины

`Shape factor for laminar flow viscous friction` - Коэффициент трения для ламинарных течений
`64` (по умолчанию) | положительный безюнитный скаляр

`Laminar flow upper Reynolds number limit` - число Рейнольдса, ниже которого поток ламинарен
`2e+3` (по умолчанию) | положительный безюнитный скаляр

`Turbulent flow lower Reynolds number limit` - число Рейнольдса, выше которого поток турбулентен
`4e+3` (по умолчанию) | положительный безюнитный скаляр

`Nominal mass flow rate` - Массовый расход жидкости из трубопровода
`[0.1 1] kg/s` (по умолчанию) | скаляр или вектор чисел в единицах измерения массы/времени

`Nominal pressure drop` - Перепад давления по трубопроводу
`[0.001 0.01] MPa` (по умолчанию) | скаляр или вектор чисел в единицах измерения давления

`Nusselt number for laminar flow heat transfer` - число Нуссельта для использования в расчетах теплопередачи для ламинарных течений
`3.66` (по умолчанию)

`Nominal mass flow rate` - Массовый расход жидкости из трубопровода
`[0.1 1] kg/s` (по умолчанию) | скаляр или вектор чисел в единицах измерения массы/времени

`Nominal inflow temperature` - Температура входного отверстия трубопровода
`[293.15 293.15] K` (по умолчанию) | скаляр или вектор чисел в единицах измерения температуры

`Nominal outflow temperature` - Температура на выходе трубопровода
`[300 300] K`'(по умолчанию) | скаляр или вектор чисел в единицах измерения температуры

`Nominal inflow pressure` - Давление на входе в трубопровод
`[0.101325 0.101325] MPa` (по умолчанию) | скаляр или вектор чисел в единицах измерения давления

`Nominal wall temperature` - Температура стенки трубопровода
`[303.15 303.15] K` (по умолчанию) | скаляр или вектор чисел в единицах измерения температуры

`Coefficient a` - Эмпирическая постоянная a корреляции Диттуса-Болтера
`0.023` (по умолчанию) | положительный безюнитный скаляр

`Exponent b` - Эмпирическая постоянная b корреляции Диттуса-Болтера
`0.8` (по умолчанию) | положительный безюнитный скаляр

`Exponent c` - Эмпирическая постоянная c корреляции Диттуса-Болтера
`0.4` (по умолчанию) | положительный безюнитный скаляр

`Colburn factor vector` - Коэффициенты Колбёрна, при которых табличные числа Рейнольдса
`[0.019 0.013 0.002]` (по умолчанию) | вектор положительных бесчисленных чисел

`Reynolds number vector for Nusselt number` - число Рейнольдса, при котором можно свести в таблицу число Нуссельта
`[100 150 100]` (по умолчанию) | вектор положительных бесчисленных чисел

`Prandtl number vector for Nusselt number` - числа Прандтля, при которых можно свести в таблицу число Нуссельта
`[1 10]` (по умолчанию) | вектор положительных бесчисленных чисел

`Nusselt number table` - числа Нуссельта по табличным числам Рейнольдса и Прандтля
`[ 3.72 4.21; 3.75 4.44; 4.21 7.15 ]` (по умолчанию) | матрица положительных бесчисленных чисел

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®