Этот раздел использует пример Нелинейная Электромеханическая Схема с Решателем Разбиения, чтобы предоставить углубленный анализ функциональности решателя Разбиения. Он исследует различные типы разбиений и их уравнения и объясняет, как решатель Разбиения решает их, чтобы получить более быструю симуляцию.
Чтобы открыть пример модели Нелинейной Электромеханической Схемы с Решателем Разбиения, введите ssc_nonlinear_electromechanical_circuit в MATLAB® Командное окно.
Чтобы просмотреть статистику модели, в окне модели, на вкладке Debug, нажмите Simscape > Statistics Viewer. При необходимости нажмите кнопку Refresh на панели инструментов окна средства просмотра, чтобы заполнить средство просмотра данными.
Разверните узел Number of partitions.
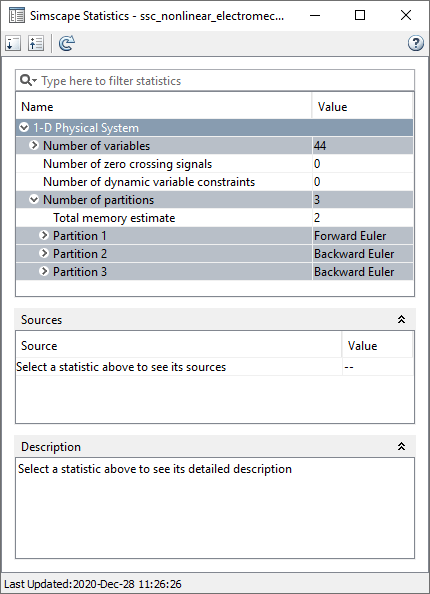
Это показывает, что решатель разделяет систему на три раздела. Первый раздел решается с помощью метода Forward Euler, а два других раздела решаются с помощью метода Backward Euler.
Выбирая Number of variables под каждым из узлов раздела, можно увидеть имена переменных, которые относятся к этому разделу.
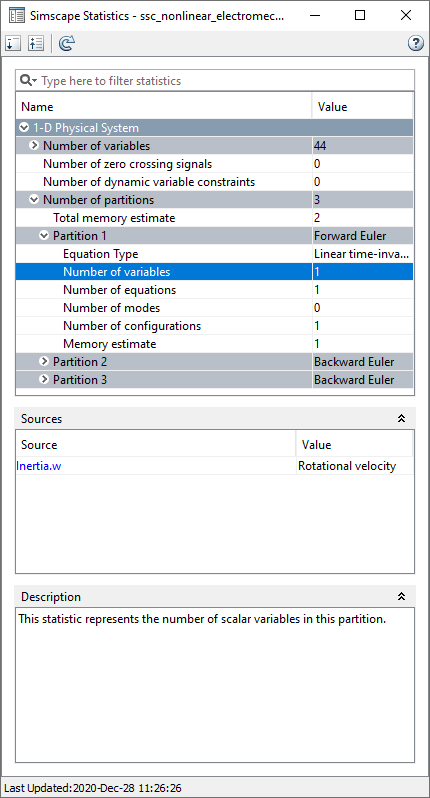
Разделу 1 принадлежит Inerta.w переменная, которая представляет скорость вращения блока Inertia.
Разделу 2 принадлежат Diode.v и Sensing.Ideal Rotational Motion Sensor.phi, и Partition 3 владеет Inerta.t. Каждый раздел отвечает за обновление значений переменных состояния, которым он владеет.
Statistics Viewer также содержит ссылки на уравнения в каждом разделе.
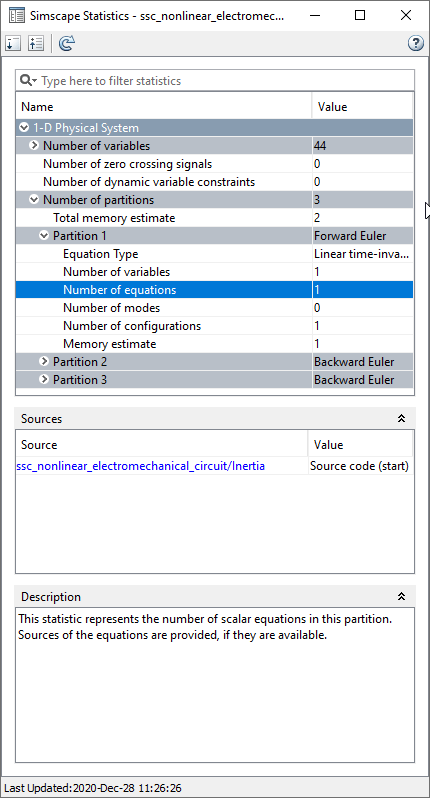
Например, если вы выбираете Number of equations в Разделе 1, а затем кликните ssc_nonlinear_electromechanical_circuit/Inertia ссылка под Source, исходный код для блоков Inertia открывается в редакторе MATLAB, указывая на это уравнение:
t == inertia * w.der;
Точно так же можно увидеть уравнения для других разбиений.
Решатель Разбиения собирает все эти уравнения в систему уравнений, необходимую для симуляции модели:
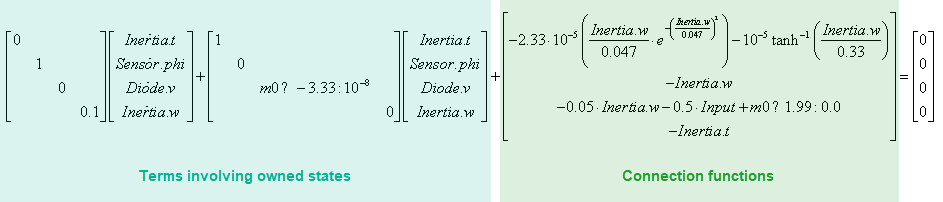
Здесь Sensor.phi - сокращение Sensing.Ideal Rotational Motion Sensor.phi переменная (используется, чтобы сделать представление системы уравнений более компактным). m0 является булевым, берущим начало из уравнения в блоке Diode, где Diode.v сравнивается с Forward voltage:
if v > Vf
i == (v - Vf*(1-Ron*Goff))/Ron;
else
i == v*Goff;
end
Сравнивая эту систему уравнений с данными Statistics Viewer, можно увидеть, что первая строка системы находится в Partition 3, потому что Partition 3 владеет Inerta.t переменная состояния. Точно так же вторая и третья строки находятся в разделе 2, а четвертая строка находится в разделе 1.
Тип уравнения разбиения зависит только от условий, связанных с принадлежащими состояниями, и не зависит от функции соединения. Для примера Partition 3 списков свою Equation Type как Linear time-invariant, несмотря на нелинейность в термине функции соединения, потому что она является линейной инвариантной во времени относительно принадлежащих ей состояний.
Во время симуляции решатель Partitioning решает разделы в том же порядке, в котором они перечислены в Statistics Viewer (то есть снизу вверх в системе уравнений), с помощью заданного метода (Forward Euler или Backward Euler). Решатель использует обновленные значения состояния, полученные после решения каждого раздела, чтобы выполнить обновление состояния для вышестоящих разделов.