Моделируйте движение платформы с помощью объектов траектории

В этом разделе описывается, как использовать три различных объекта траектории для моделирования траекторий платформы и как выбрать между ними.

Введение

Radar Toolbox™ предоставляет три системных объектов, которые можно использовать для моделирования траекторий платформ, включая наземные транспортные средства, корабли, самолеты и космические аппараты. Можно выбрать между этими объектами траектории на основе доступной информации о траектории и диапазоном расстояний траектории.

waypointTrajectory (Sensor Fusion and Tracking Toolbox) - задает траекторию с помощью нескольких путевых точек в Декартовых координатах, через которые должна пройти траектория. Траектория предполагает, что опорная система координат является фиксированной системой координат North-East-Down (NED) или East-North-Up (ENU). Поскольку интерполяция траектории принимает, что ускорение свободного падения, выраженное в опорной системе координат траектории, является постоянным, waypointTrajectory обычно используется для траектории, заданной в области, которая охватывает только десятки или сотни километров.
geoTrajectory (Sensor Fusion and Tracking Toolbox) - задает траекторию с помощью нескольких путевых точек в геодезических координатах (широта, долгота и высота), через которые должна проходить траектория. Поскольку путевые точки выражены в геодезических координатах, geoTrajectory обычно используется для траектории от сотен до тысяч километров расстояния.
kinematicTrajectory (Sensor Fusion and Tracking Toolbox) - задает траекторию, используя кинематические свойства, такие как ускорение и угловое ускорение, выраженные в каркасе кузова платформы. Можно использовать kinematicTrajectory чтобы сгенерировать траекторию любого диапазона расстояний, пока доступна кинематическая информация траектории. Объект принимает Декартову опорную систему координат.

Два объекта траектории на основе путевой точки (waypointTrajectory и geoTrajectory) может автоматически вычислить информацию линейной скорости платформы, но можно также явным образом задать линейную скорость с помощью Velocity свойство или комбинация Course, GroundSpeed, и ClimbRate свойства.

Траектория платформы состоит из вращательного движения и поступательного движения. По умолчанию два объекта траектории на основе путевой точки (waypointTrajectory и geoTrajectory) автоматически генерировать ориентацию платформы в каждой точке пути путем выравнивания угла рыскания по пути траектории, но можно явным образом задать ориентацию с помощью Orientation свойство. Также можно использовать AutoPitch и AutoBank свойства для включения автоматических углов тангажа и крена, соответственно. Для kinematicTrajectory, вам нужно использовать Orientation свойство и вход скорости вращения для задания вращательного движения траектории.

`waypointTrajectory`

The waypointTrajectory Системный объект задает траекторию, которая плавно проходит через путевые точки, выраженные в Декартовых координатах. Обычно можно использовать waypointTrajectory для моделирования транспортных средств, путешествующих в пределах сотен километров. Эти транспортные средства включают автомобили, наземные морские суда и коммерческие самолеты (вертолеты, самолеты и квадрокоптеры). Можно выбрать опорную систему координат как фиксированную систему координат ENU или NED с помощью ReferenceFrame свойство. Для получения дополнительной информации о том, как объект генерирует траекторию, смотрите раздел «Алгоритмы (Sensor Fusion and Tracking Toolbox)» waypointTrajectory.

`waypointTrajectory` Пример посадки самолета

Открыть Live Script

Определите траекторию посадочного самолета с помощью waypointTrajectory объект.

waypoints = [-421 -384 2000;
    47 -294 1600;
    1368 174 1300;
    995 1037 900;
    -285 293 600;
    -1274 84 350;
    -2328 101 150;
    -3209 83 0];
timeOfArrival =  [0; 16.71; 76.00; 121.8; 204.3; 280.31; 404.33; 624.6];
aircraftTraj = waypointTrajectory(waypoints,timeOfArrival);

Создайте theaterPlot объект для визуализации траектории и самолета.

minCoords = min(waypoints);
maxCoords = max(waypoints);
tp = theaterPlot('XLimits',1.2*[minCoords(1) maxCoords(1)], ...
    'YLimits',1.2*[minCoords(2) maxCoords(2)], ...
    'ZLimits',1.2*[minCoords(3) maxCoords(3)]);

% Create a trajectory plotter and a platform plotter
tPlotter = trajectoryPlotter(tp,'DisplayName','Trajectory');
pPlotter = platformPlotter(tp,'DisplayName','Aircraft');

Получите Декартовы путевые точки траектории с помощью lookupPose функция объекта.

sampleTimes = timeOfArrival(1):timeOfArrival(end);
numSteps = length(sampleTimes);
[positions,orientations] = lookupPose(aircraftTraj,sampleTimes);
plotTrajectory(tPlotter,{positions})
axis equal

Постройте график движения платформы с помощью объекта mesh самолета.

mesh = scale(rotate(tracking.scenario.airplaneMesh,[0 0 180]),15); % Exaggerated scale for better visualization
view(20.545,-20.6978)
for i = 1:numSteps
    plotPlatform(pPlotter,positions(i,:),mesh,orientations(i))
    % Uncomment the next line to slow the aircraft motion animation
    % pause(1e-7)
end

В анимации угол рыскания самолета по умолчанию выравнивается по траектории.

Создайте вторую траекторию самолета с теми же путевыми точками, что и первая траектория самолета, но установите ее AutoPitch и AutoBank свойства для true. Это генерирует траекторию, более показательную для возможных маневров самолета.

aircraftTraj2 = waypointTrajectory(waypoints,timeOfArrival, ...
    'AutoPitch',true, ...
    'AutoBank',true);

Постройте график второй траектории и наблюдайте изменение ориентации самолета.

[positions2,orientations2] = lookupPose(aircraftTraj2,sampleTimes);
for i = 1:numSteps
    plotPlatform(pPlotter,positions2(i,:),mesh,orientations2(i));
    % Uncomment the next line to slow the aircraft motion animation
    % pause(1e-7)
end

Figure contains an axes. The axes contains 2 objects of type line. These objects represent Trajectory, Aircraft.

Визуализируйте различия ориентации между двумя траекториями в углах.

distance = dist(orientations2,orientations);
figure
plot(sampleTimes,distance*180/pi)
xlabel('Time (sec)')
ylabel('Angular Ditance (dge)')
title('Orientation Difference Between Two Waypoint Trajectories')

Figure contains an axes. The axes with title Orientation Difference Between Two Waypoint Trajectories contains an object of type line.

`geoTrajectory`

The geoTrajectory Системный объект генерирует траекторию, используя путевые точки таким же образом, как и waypointTrajectory объект, но он имеет два основных различия в том, как задать путевые точки и входы скорости.

При указании путевых точек для geoTrajectory, выражают каждую путевую точку в геодезических координатах широты, долготы и высоты над WG84 эллипсоидной моделью. Используя геодезические координаты, можно удобно задать дальние траектории, такие как траектория рейса самолета на реалистичной модели Земли.
При определении информации о ориентации и скорости для каждой путевой точки опорной системой координат для ориентации и скорости является локальная система координат NED или ENU, заданная под текущей точкой пути траектории. Например, N 1- E ₁- D 1 кадр, показанный на рисунке, является локальной опорной рамкой NED.

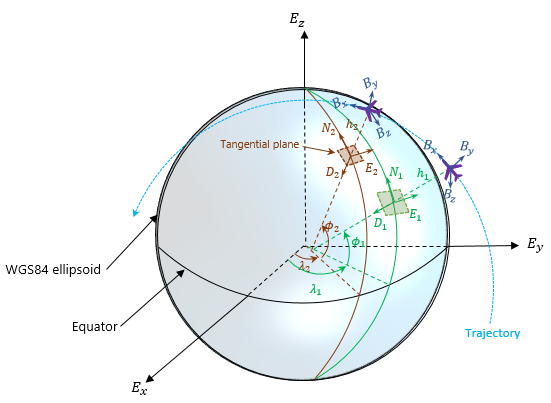
На рисунке,

<reservedrangesplaceholder5> <reservedrangesplaceholder4>, <reservedrangesplaceholder3> <reservedrangesplaceholder2> и <reservedrangesplaceholder1> <reservedrangesplaceholder0> - три оси системы координат Сосредоточенного на земле зафиксированного к земле (ECEF), которая закреплена на Земле.
(λ 1, _ϕ 1, h 1) и (λ ₂, ϕ 2, h 2) являются геодезическими координатами плоскости в двух путевых точках.
(N 1, _E 1, D 1) и (N ₂, E 2, D 2) являются двумя локальными кадрами NED, соответствующими двум путевым точкам траектории.
<reservedrangesplaceholder5> <reservedrangesplaceholder4>, <reservedrangesplaceholder3> <reservedrangesplaceholder2> и <reservedrangesplaceholder1> <reservedrangesplaceholder0> - три оси каркаса кузова платформы, который закреплен на платформе.

geo `Trajectory` Пример для траектории рейса

Открыть Live Script

Загрузите рейс данные траектории рейса из Лос-Анджелеса в Бостон. Данные содержат информацию о рейсе, включая время рейса, геодезические координаты для каждой путевой точки, курса и наземной скорости.

load flightData.mat

Создайте geoTrajectory объект на основе рейса данных.

planeTraj = geoTrajectory([latitudes longitudes heights],timeOfArrival, ...
    'Course',courses,'GroundSpeed',speeds);

Проверьте Декартовы координаты путевых точек в системе координат ECEF.

sampleTimes = 0:1000:3600*10;
positionsCart = lookupPose(planeTraj,sampleTimes,'ECEF');

Отобразите траекторию с помощью helperGlobeView класс, который аппроксимирует сферу Земли.

viewer = helperGlobeView;
plot3(positionsCart(:,1),positionsCart(:,2),positionsCart(:,3),'r')

Можно дополнительно исследовать траекторию, запросив другие выходы траектории.

`kinematicTrajectory`

В отличие от двух объектов траектории путевой точки, kinematicTrajectory Системный объект использует кинематические атрибуты, чтобы задать траекторию. Представьте траекторию как численное интегрирование положения (положение и ориентация) и линейной скорости платформы, основанное на информации линейного ускорения и углового ускорения. Положение и линейная скорость заданы с учетом выбранной, фиксированной системы координат сценария, в то время как линейное ускорение и скорость вращения заданы с учетом каркаса кузова платформы.

`kinematicTrajectory` Пример для пути к БПЛА

Открыть Live Script

Создайте kinematicTrajectory объект для симуляции пути БПЛА. Задайте временной интервал траектории как 120 секунд.

traj = kinematicTrajectory('SampleRate',1, ...
    'AngularVelocitySource','Property');

tStart = 0;
tFinal = 120;
tspan = tStart:tFinal;

numSteps = length(tspan);
positions = NaN(3,numSteps);
velocities = NaN(3,numSteps);
vel = NaN(1,numSteps);

Чтобы сформировать квадратный путь, охватывающий небольшую область, разделите траекторию БПЛА на шесть сегментов:

Взлет и подъем в z-направлении
Движение в положительном направлении x
Движение в положительном направлении y
Движение в отрицательном направлении X
Движение в отрицательном направлении y
Спуск в z-направлении и посадка

В каждом сегменте БПЛА ускоряется в одном направлении и затем замедляется в этом направлении с той же величиной ускорения. В результате в конце каждого сегмента скорость БПЛА равна нулю.

segSteps = floor(numSteps/12);
accelerations = zeros(3,numSteps);
acc = 1;
% Acceleration for taking off and ascending in the z-direction
accelerations(3,1:segSteps) = acc;
accelerations(3,segSteps+1:2*segSteps) = -acc;

% Acceleration for moving in the positive x-direction
accelerations(1,2*segSteps+1:3*segSteps) = acc;
accelerations(1,3*segSteps+1:4*segSteps) = -acc;

% Acceleration for moving in the positive y-direction
accelerations(2,4*segSteps+1:5*segSteps) = acc;
accelerations(2,5*segSteps+1:6*segSteps) = -acc;

% Acceleration for moving in the negative x-direction
accelerations(1,6*segSteps+1:7*segSteps) = -acc;
accelerations(1,7*segSteps+1:8*segSteps) = acc;

% Acceleration for moving in the negative y-direction 
accelerations(2,8*segSteps+1:9*segSteps) = -acc;
accelerations(2,9*segSteps+1:10*segSteps) = acc;

% Descending in the z-direction and landing
accelerations(3,10*segSteps+1:11*segSteps) =-acc;
accelerations(3,11*segSteps+1:end) = acc;

Симулируйте траекторию путем вызова kinematicTrajectory объект с заданным ускорением.

for i = 1:numSteps
    [positions(:,i),~,velocities(:,i)] = traj(accelerations(:,i)');  
     vel(i) = norm(velocities(:,i));
end

Визуализируйте траекторию с помощью theaterPlot.

% Create a theaterPlot object and create plotters for the trajectory and the
% UAV Platform.
figure
tp = theaterPlot('XLimits',[-30 130],'YLimits',[-30 130],'ZLimits',[-30 130]);
tPlotter = trajectoryPlotter(tp,'DisplayName','UAV trajectory');
pPlotter = platformPlotter(tp,'DisplayName','UAV','MarkerFaceColor','g');

% Plot the trajectory.
plotTrajectory(tPlotter,{positions'})
view(-43.18,56.49)

% Use a cube to represent the UAV platform.
dims = struct('Length',10, ...
    'Width',5, ...
    'Height',3, ...
    'OriginOffset',[0 0 0]);

% Animate the UAV platform position.
for i = 1:numSteps
    plotPlatform(pPlotter,positions(:,i)',dims,eye(3))
    pause(0.01)
end

Figure contains an axes. The axes contains 2 objects of type line. These objects represent UAV trajectory, UAV.

Показать скоростную величину платформы БПЛА.

figure
plot(tspan,vel)
xlabel('Time (s)')
ylabel('Velocity (m/s)')
title('Magnitude of the UAV Velocity')

Figure contains an axes. The axes with title Magnitude of the UAV Velocity contains an object of type line.

`kinematicTrajectory` Пример для траектории самолета

Открыть Live Script

Использование kinematicTrajetory для задания круговой траектории космического аппарата. Орбита имеет следующие элементы:

Орбитальный радиус ( $r$ ) - 7000 км
Наклонение ( $i$ ) - 60 степени
Аргумент восходящего узла ( $Ω$ ) - 90 степени. Направление восходящего узла выровнено с $Y$ -направление.
Истинная аномалия ( $ν$ ) - -90 степени

На рисунке, $X$ - $Y$ - $Z$ - ориентированная на Землю инерционная (ECI) система координат, которая имеет фиксированное положение и ориентацию в пространстве. $x$ - $y$ - $z$ - каркас кузова космического аппарата, закрепленная на космическом аппарате. $\vec{r}$ и $\vec{v}$ являются начальным положением и скоростью космического аппарата.

Чтобы задать круговую орбиту с помощью kinematicTrajectory, необходимо обеспечить начальное положение, начальную скорость и начальную ориентацию космического аппарата относительно системы координат ECI. Для выбранной истинной аномалии ( $v$ = – $90^{\circ}$ ), скорость космического аппарата выровнена с $Y$ -направление.

inclination = 60; % degrees
mu = 3.986e14; % standard earth gravitational parameter
radius = 7000e3;% meters
v = sqrt(mu/radius); % speed
initialPosition = [radius*cosd(inclination),0,-radius*sind(inclination)]';
initialVelocity = [0 v 0]';

Предположим, что направление X каркаса кузова космического аппарата является радиальным направлением, направление z является нормальным направлением плоскости орбиты, и направление Y завершает правило правой руки. Используйте допущения, чтобы задать ориентацию каркаса кузова в исходном положении.

orientation = quaternion([0 inclination 0],'eulerd','zyx','frame');

Выразите скорость вращения и угловое ускорение траектории в каркасе кузова платформы.

omega = v/radius;
angularVelocity = [0 0 omega]';
a = v^2/radius;
acceleration = [-a 0 0]';

Установите время симуляции одного орбитального периода. Задайте шаг симуляции 2 секунды.

tFinal = 2*pi/omega;
dt = 2;
sampleRate = 1/dt;
tspan = 0:dt:tFinal;
numSteps = length(tspan);

Создайте траекторию самолета. Поскольку ускорение и скорость вращения космического аппарата остаются постоянными относительно каркаса кузова космического аппарата, задайте их как константы. Сгенерируйте выходы положения и ориентации вдоль траектории при помощи kinematicTrajectory объект.

traj = kinematicTrajectory('SampleRate',sampleRate, ...
    'Position',initialPosition, ...
    'Velocity',initialVelocity, ...
    'Orientation',orientation, ...
    'AngularVelocity',angularVelocity, ...
    'Acceleration',acceleration, ...
    'AccelerationSource','Property', ...
    'AngularVelocitySource','Property');

% Generate position and orientation outputs.
positions = NaN(3,numSteps);
orientations = zeros(numSteps,1,'quaternion');
for i = 1:numSteps    
   [positions(:,i),orientations(i)] = traj();     
end

Используйте helperGlobeView класс и theaterPlot для отображения траектории.

viewer = helperGlobeView(0,[60 0]);
tp = theaterPlot('Parent',gca,...
    'XLimits',1.2*[-radius radius],...
    'YLimits',1.2*[-radius radius],...
    'ZLimits',1.2*[-radius radius]);
tPlotter = trajectoryPlotter(tp,'LineWidth',2);
pPlotter = platformPlotter(tp,'MarkerFaceColor','m');
legend(gca,'off')

plotTrajectory(tPlotter,{positions'})
% Use a cube with exaggerated dimensions to represent the spacecraft.
dims = struct('Length',8e5,'Width',4e5,'Height',2e5,'OriginOffset',[0 0 0]);

for i = 1:numSteps    
   plotPlatform(pPlotter,positions(:,i)',dims,orientations(i))
   % Since the reference frame is the ECI frame, earth rotates with respect to it.
   rotate(viewer,dt)
end

Сводные данные

В этом разделе вы научились использовать три объекта траектории для настройки собственных траекторий на основе доступной информации. В сложение вы узнали фундаментальные различия в их применении. В этой таблице выделены основные атрибуты этих объектов траектории.

Объект траектории	Входные параметры положения	Входные параметры линейной скорости	Ориентация	Входные параметры ускорения и скорости вращения	Рекомендуемый диапазон расстояний
`waypointTrajectory`	Декартовы путевые точки, выраженные в фиксированной системе координат (NED или ENU)	Один из следующих опций: Автоматически сгенерируйте скорость для плавной траектории, по умолчанию Задайте скорость в фиксированной системе координат в каждой точке пути Задайте курс, наземную скорость и скорость набора высоты в фиксированной системе координат в каждой путевой точке	Один из следующих опций: Автоматическое рыскание по умолчанию, автоматическое тангаж по выбору и автоматическое рыскание по выбору Задайте ориентацию в фиксированной системе координат	Невозможно задать	От десятков до сотен километров
`geoTrajectory`	Геодезические путевые точки в системе координат ECEF	Один из следующих опций: Автоматически сгенерируйте скорость для плавной траектории, по умолчанию Задайте скорость в локальной системе координат (NED или ENU) для каждой путевой точки Укажите курс, скорость земли и скорость набора высоты в локальной системе координат (NED или ENU) для каждой путевой точки	Один из следующих опций: Автоматическое рыскание по умолчанию, автоматическое тангаж по выбору и автоматическое рыскание по выбору Задайте ориентацию в локальной системе координат	Невозможно задать	От сотен до тысяч километров
`kinematicTrajectory`	Начальное положение, выраженное в выбранной фиксированной системе координат	Только начальная скорость в фиксированной системе координат	Только начальная ориентация в фиксированной системе координат	Задайте ускорение и скорость вращения в каркасе кузова платформы	Неограниченный диапазон расстояний

Документация