Пакет Reinforcement Learning Toolbox™ предоставляет несколько предопределенных окружений систем управления, для которых уже заданы действия, наблюдения, вознаграждения и динамика. Можно использовать эти окружения для:
Изучения концепций обучения с подкреплением.
Ознакомьтесь с функциями пакета Reinforcement Learning Toolbox.
Тестирования своих агентов обучения с подкреплением.
Можно загрузить следующий предопределенный MATLAB® управляйте окружениями системы, используя rlPredefinedEnv функция.
| Окружение | Задача агента |
|---|---|
| Тележка с шестом | Балансировка шеста на движущейся тележке путем приложения сил к тележке с помощью дискретного или непрерывного пространства действия. |
| Двойной интегратор | Управляйте динамической системой второго порядка, используя дискретное или непрерывное пространство действий. |
| Математический маятник с наблюдением изображений | Качание вверх и балансировка простого маятника с помощью дискретного или непрерывного пространства действий. |
Можно также загрузить предопределённые окружения мира сетки MATLAB. Для получения дополнительной информации смотрите Загрузка предопределённых окружений мира сетки.
Цель агента в предопределенных окружениях тележки с шестом - сбалансировать шест на движущейся тележке, прикладывая горизонтальные силы к тележке. Считается, что шест успешно сбалансирован, если оба из следующих условий удовлетворены:
Угол шеста остается внутри заданного порога вертикального положения, где вертикальное положение соответствует углу ноль радиан.
Величина положения тележки остается ниже заданного порога.
Существует два варианта окружения тележки с шестом, которые различаются пространством действий агента.
Дискретный - Агент может применить силу Fmax или - Fmax к тележке, где Fmax является MaxForce свойство окружения.
Непрерывный - Агент может приложить любую силу в область значений [- Fmax, Fmax].
Чтобы создать окружение тележки с шестом, используйте rlPredefinedEnv функция.
Дискретное пространство действий
env = rlPredefinedEnv('CartPole-Discrete');Непрерывное пространство действий
env = rlPredefinedEnv('CartPole-Continuous');Вы можете визуализировать окружение тележки с шестом, используя plot функция. График отображает тележку в виде синего квадрата, а шест в виде красного прямоугольника.
plot(env)
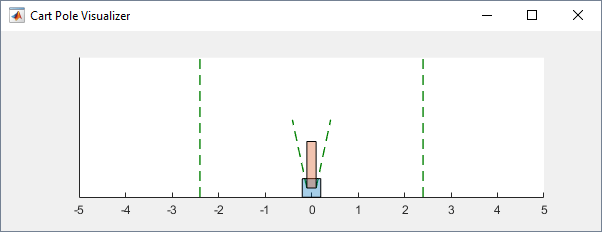
Чтобы визуализировать окружение во время обучения, позвоните plot перед обучением и сохраните рисунок визуализации открытой.
Для примеров, показывающих, как обучить агентов в окружениях тележки с шестом, смотрите следующее:
| Свойство | Описание | Дефолт |
|---|---|---|
Gravity | Ускорение из-за силы тяжести в метрах в секунду | 9.8 |
MassCart | Масса тележки в килограммах | 1 |
MassPole | Масса шеста в килограммах | 0.1 |
Length | Половина длины шеста в метрах | 0.5 |
MaxForce | Максимальная горизонтальная величина силы в ньютонах | 10 |
Ts | Шаг расчета в секундах | 0.02 |
ThetaThresholdRadians | Порог угла шеста в радианах | 0.2094 |
XThreshold | Порог положения тележки в метрах | 2.4 |
RewardForNotFalling | Вознаграждение за каждый временной шаг полюс сбалансирован | 1 |
PenaltyForFalling | Вознаграждение штраф за неспособность сбалансировать полюс | Дискретный - Непрерывный - |
State | Состояние окружения, заданное как вектор-столбец со следующими переменными состояния:
| [0 0 0 0]' |
В окружениях тележки с шестом агент взаимодействует со средой с помощью единственного сигнала действия - горизонтальной силы, приложенной к тележке. Окружение содержит объект спецификации для этого сигнала действия. Для окружения с:
Дискретное пространство действий, спецификация является rlFiniteSetSpec объект.
Непрерывное пространство действий, спецификация является rlNumericSpec объект.
Для получения дополнительной информации о получении спецификаций действий от окружения см. getActionInfo.
В системе тележки с шестом агент может наблюдать все переменные состояния окружения в env.State. Для каждой переменной состояния окружение содержит rlNumericSpec спецификация наблюдений. Все состояния непрерывны и неограниченны.
Для получения дополнительной информации о получении спецификаций наблюдений из окружения, см. getObservationInfo.
Сигнал вознаграждения для этого окружения состоит из двух компонентов.
Положительное вознаграждение для каждого временного шага, когда полюс сбалансирован, то есть тележка и полюс оба остаются в пределах своих заданных пороговых областей значений. Это вознаграждение накапливается за весь эпизод тренировки. Чтобы контролировать размер этого вознаграждения, используйте RewardForNotFalling свойство окружения.
Однократный отрицательный штраф, если либо шест, либо тележка перемещаются за пределы своей пороговой области значений. На данной точке эпизод тренировки останавливается. Чтобы контролировать размер этого штрафа, используйте PenaltyForFalling свойство окружения.
Цель агента в предопределённых окружениях двойного интегратора состоит в том, чтобы управлять положением массы в системе второго порядка путем применения входного параметра силы. В частности, система второго порядка является двойным интегратором с усилением.
Эпизоды тренировки для этих окружений заканчиваются, когда происходит одно из следующих событий:
Масса выходит за заданный порог от источника.
Норма вектора состояний меньше заданного порога.
Существует два варианта окружения двойного интегратора, которые различаются пространством действий агента.
Дискретный - Агент может применить силу Fmax или - Fmax к тележке, где Fmax является MaxForce свойство окружения.
Непрерывный - Агент может приложить любую силу в область значений [- Fmax, Fmax].
Чтобы создать окружение двойного интегратора, используйте rlPredefinedEnv функция.
Дискретное пространство действий
env = rlPredefinedEnv('DoubleIntegrator-Discrete');Непрерывное пространство действий
env = rlPredefinedEnv('DoubleIntegrator-Continuous');Вы можете визуализировать окружение двойного интегратора, используя plot функция. На графике масса отображается в виде красного прямоугольника.
plot(env)
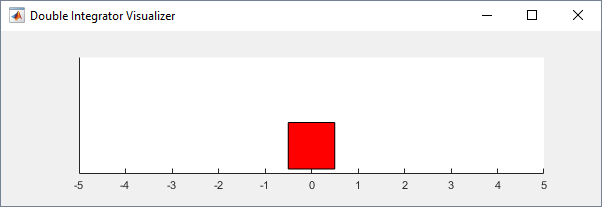
Чтобы визуализировать окружение во время обучения, позвоните plot перед обучением и сохраните рисунок визуализации открытой.
Для примеров, показывающих, как обучить агентов в окружениях двойного интегратора, смотрите следующее:
| Свойство | Описание | Дефолт |
|---|---|---|
Gain | Усиление для double-интегратора | 1 |
Ts | Шаг расчета в секундах | 0.1 |
MaxDistance | Порог величины расстояния в метрах | 5 |
GoalThreshold | Порог нормы состояния | 0.01 |
Q | Матрица веса для компонента наблюдения сигнала вознаграждения | [10 0; 0 1] |
R | Матрица веса для компонента действия сигнала вознаграждения | 0.01 |
MaxForce | Максимальная входная сила в ньютонах | Дискретный: Непрерывный: |
State | Состояние окружения, заданное как вектор-столбец со следующими переменными состояния:
| [0 0]' |
В окружениях двойного интегратора агент взаимодействует со средой с помощью единственного сигнала действия - силы, приложенной к массе. Окружение содержит объект спецификации для этого сигнала действия. Для окружения с:
Дискретное пространство действий, спецификация является rlFiniteSetSpec объект.
Непрерывное пространство действий, спецификация является rlNumericSpec объект.
Для получения дополнительной информации о получении спецификаций действий от окружения см. getActionInfo.
В системе двойного интегратора агент может наблюдать обе переменные состояния окружения в env.State. Для каждой переменной состояния окружение содержит rlNumericSpec спецификация наблюдений. Оба состояния непрерывны и неограниченны.
Для получения дополнительной информации о получении спецификаций наблюдений из окружения, см. getObservationInfo.
Сигнал вознаграждения для этого окружения является эквивалентом в дискретном времени следующего вознаграждения в непрерывном времени, которое аналогично функции стоимости контроллера LQR.
Здесь:
Q и R являются свойствами окружения.
x - вектор состояния окружения.
u - это вход сила.
Это вознаграждение является вознаграждением эпизода, то есть совокупным вознаграждением за весь эпизод тренировки.
Это окружение является простым маятником без трения, который первоначально висит в нисходящем положении. Цель обучения состоит в том, чтобы сделать маятник вертикальным, не падая, используя минимальные усилия по управлению.
Существует два варианта окружения математического маятника, которые различаются пространством действий агента.
Дискретный - Агент может применить крутящий момент -2, -1, 0, 1, или 2 к маятнику.
Непрерывный - Агент может приложить любой крутящий момент в области значений [-2, 2].
Чтобы создать окружение математического маятника, используйте rlPredefinedEnv функция.
Дискретное пространство действий
env = rlPredefinedEnv('SimplePendulumWithImage-Discrete');Непрерывное пространство действий
env = rlPredefinedEnv('SimplePendulumWithImage-Continuous');Для примеров, показывающих, как обучить агента в этом окружении, смотрите следующее:
| Свойство | Описание | Дефолт |
|---|---|---|
Mass | Маятниковая масса | 1 |
RodLength | Длина маятника | 1 |
RodInertia | Маятниковый момент инерции | 0 |
Gravity | Ускорение из-за силы тяжести в метрах в секунду | 9.81 |
DampingRatio | Демпфирование при движении маятника | 0 |
MaximumTorque | Максимальный входной крутящий момент в ньютонах | 2 |
Ts | Шаг расчета в секундах | 0.05 |
State | Состояние окружения, заданное как вектор-столбец со следующими переменными состояния:
| [0 0 ]' |
Q | Матрица веса для компонента наблюдения сигнала вознаграждения | [1 0;0 0.1] |
R | Матрица веса для компонента действия сигнала вознаграждения | 1e-3 |
В окружениях математического маятника агент взаимодействует с окружением с помощью единственного сигнала действия - крутящего момента, приложенного к основе маятника. Окружение содержит объект спецификации для этого сигнала действия. Для окружения с:
Дискретное пространство действий, спецификация является rlFiniteSetSpec объект.
Непрерывное пространство действий, спецификация является rlNumericSpec объект.
Для получения дополнительной информации о получении спецификаций действий от окружения см. getActionInfo.
В окружении математического маятника агент получает следующие сигналы наблюдения:
50 на 50 полутоновое изображение положения маятника
Производная от угла маятника
Для каждого сигнала наблюдения окружение содержит rlNumericSpec спецификация наблюдений. Все наблюдения непрерывны и неограниченны.
Для получения дополнительной информации о получении спецификаций наблюдений из окружения, см. getObservationInfo.
Сигнал вознаграждения для этого окружения
Здесь:
θt - угол смещения маятника из вертикального положения.
является производной от угла маятника.
ut-1 - усилие по управлению от предыдущего временного шага.