Вы моделируете каждый компонент в структуре системы, чтобы представлять физическое или функциональное поведение этого компонента. Вы проверяете поведение основного компонента путем моделирования их с помощью тестовых данных.
При моделировании отдельных компонентов используется большая картина всей системы. Начните, загрузив размещение. В командной строке MATLAB введите:
open_system('system_layout.slx')

Simulink® модель компонента основана на нескольких начальных точках:
Явная математическая связь между выходом и входом физического компонента - можно вычислить выходы компонента из входов, прямо или косвенно, через алгебраические расчеты и интегрирование дифференциальных уравнений. Например, расчет уровня воды в баке с учетом скорости притока является явной зависимостью. Каждый блок Simulink выполняется на основе определения расчетов от его входов до его выходов.
Неявная математическая связь между переменными модели физического компонента - поскольку переменные взаимозависимы, присвоение входа и выхода компоненту не является простым. Для примера - напряжение на + конец двигателя, соединенный в цепь, и напряжение на - конец имеет неявную связь. Чтобы смоделировать такую зависимость в Simulink, можно либо использовать физические инструменты моделирования, такие как Simscape™, либо смоделировать эти переменные как часть большего компонента, которая позволяет определять вход/выход. Иногда более тщательный анализ целей моделирования и определений компонентов помогает задать отношения ввода/вывода.
Данные, полученные из фактической системы - Вы измерили входные/выходные данные из фактического компонента, но полностью определенной математической зависимости не существует. Многие устройства имеют немоделированные компоненты, которые соответствуют этому описанию. Например, тепло, рассеиваемое телевизором. Можно использовать System Identification Toolbox™, чтобы определить отношение вход/выход для такой системы.
Явное функциональное определение - Вы задаете выходы функционального компонента из входов через алгебраические и логические расчеты. Для примера - логика переключения термостата. Можно смоделировать большинство функциональных отношений как блоки Simulink и подсистемы.
Этот учебник моделирует физические и функциональные компоненты с явными отношениями вход/выход. В этом руководстве вы будете:
Используйте системные уравнения, чтобы создать модель Simulink.
Добавьте и соедините блоки Simulink в Редактор. Блоки представляют коэффициенты и переменные из уравнений.
Создайте модель для каждого компонента отдельно. Самый эффективный способ создать модель системы - это сначала рассмотреть компоненты независимо.
Начните с построения простых моделей с помощью аппроксимаций системы. Идентифицируйте допущения, которые могут повлиять на точность вашей модели. Итерационно добавляйте детали, пока уровень сложности не удовлетворяет требованиям моделирования и точности.
Опишите отношения между компонентами, например, данными, энергией и передачей силы. Используйте системные уравнения, чтобы создать графическую модель системы в Simulink.
Некоторые вопросы, которые нужно задать, прежде чем вы начнете моделировать компонент:
Каковы константы для каждого компонента? Какие значения не изменяются, если вы не измените их?
Каковы переменные для каждого компонента? Какие значения изменяются с течением времени?
Сколько переменных состояния имеет компонент?
Выведите уравнения для каждого компонента используя научные принципы. Многие системные уравнения делятся на три категории:
Для непрерывных систем дифференциальные уравнения описывают скорость изменения для переменных с уравнениями, заданными для всех значений времени. Для примера дифференциальное уравнение первого порядка задает скорость автомобиля:
Для дискретных систем разностные уравнения описывают скорость изменения для переменных, но уравнения заданы только в определенные моменты времени. Для примера, управляющий сигнал от дискретного пропорционально-производного контроллера:
Уравнения без производных являются алгебраическими уравнениями. Для примера алгебраическое уравнение задает полный ток в параллельной схеме с двумя компонентами:
Колеса и линейное движение. Существуют две силы, которые действуют на колесо:
Сила, приложенная двигателем - сила F действующая в направлении изменения скорости и являющаяся входом к подсистемам колеса.
Сила сопротивления - сила Fdrag действующая против направления изменения скорости и являющаяся функцией скорости.
Ускорение пропорционально сумме этих сил:
Где kdrag - коэффициент сопротивления, а m - масса робота. Каждое колесо несет половину этой массы.
Создайте модель колеса:
В system_layout дважды кликните подсистему Right Wheel, чтобы отобразить пустую подсистему.
Моделируйте скорость и ускорение. Добавьте блок Integrator. Оставьте начальное условие установленным на 0. Входом этого блока является Vdot ускорения, а выходом - V скорости.
![]()
Моделируйте силу перетаскивания. Добавьте блок MATLAB Function из библиотеки User-Defined Functions. Блок MATLAB Function обеспечивает быстрый способ реализации математических выражений в вашей модели. Чтобы отредактировать функцию, дважды кликните блок, чтобы открыть Редактор функций MATLAB.
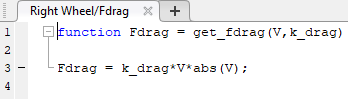
Задайте аргументы для блока MATLAB Function. В редакторе MATLAB Function блоков нажмите
кнопку Edit Data. Щелкните k_drag, установите![]() Scope равным Parameter и нажмите Apply.
Scope равным Parameter и нажмите Apply.
Вычесть силу перетаскивания из силы двигателя Subtract блоком. Завершите уравнение сила-ускорение с помощью Gain блока с параметром 1/(m/2).
Чтобы изменить направление блока MATLAB Function, щелкните правой кнопкой мыши блок и выберите Rotate & Flip > Flip Block. Соедините блоки.
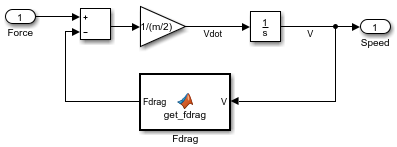
Динамика двух колес одинаковая. Создайте копию только что смоделированной подсистемы Правого колеса и вставьте ее в подсистему Левого колеса.
Просмотрите верхний уровень модели. Нажмите кнопку Navigate Up To Parent .![]()
Вращательное Движение. Когда два колеса поворачиваются в противоположных направлениях, они перемещаются по кругу радиуса r, вызывая вращательное движение робота. При повороте колес в том же направлении вращения нет. Принимая, что скорости колеса всегда равны по величине, практично смоделировать вращательное движение как зависимое от различия двух скоростей колеса VR и VL:
Создайте модель динамики вращения:
На верхнем уровне system_layout дважды кликните подсистему Вращение, чтобы отобразить пустую подсистему. Удалите соединение между блоками Inport и Outport.
Моделируйте угловую скорость и угол. Добавьте блок Integrator. Оставьте начальное условие установленным на 0. Выходом этого блока является угол theta а входом - theta_dot угловой скорости.
Вычислите угловую скорость от тангенциальной скорости. Добавьте Gain с 1/(2*r) параметра.
Соедините блоки.

Просмотрите верхний уровень модели. Нажмите кнопку Navigate Up To Parent .![]()
Опишите функцию от входа функции до ее выхода. Это описание может включать алгебраические уравнения и логические конструкции, которые можно использовать, чтобы создать графическую модель системы в Simulink.
Преобразование координат. Скорость робота в координатах X и Y, VX и VY, связана с линейной VN скорости и theta угла:
Создайте модель координатного преобразования:
На верхнем уровне system_layout дважды кликните подсистему Преобразования координат, чтобы отобразить пустую подсистему.
Моделируйте тригонометрические функции. Добавьте блок SinCos из библиотеки Математические операции.
Моделируйте умножения. Добавьте два блока Product из библиотеки Математические операции.
Соедините блоки.
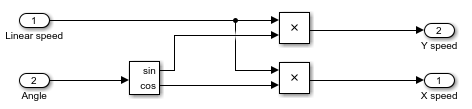
Просмотрите верхний уровень модели. Нажмите кнопку Navigate Up To Parent .![]()
Источником для значений параметров модели может быть:
Письменные спецификации, такие как таблицы стандартных свойств или таблицы данных производителя
Прямые измерения в существующей системе
Оценки с использованием системного ввода/вывода
Эта модель использует эти параметры:
| Параметр | Символ | Значение |
|---|---|---|
| Масса | m | 2,5 кг |
| Сопротивление качению | k_drag | 30 Нс2/ м |
| Радиус робота | r | 0,15 м |
Simulink использует MATLAB® рабочая область для оценки параметров. Установите эти параметры в командном окне MATLAB:
m = 2.5; k_drag = 30; r = 0.15;
Проверьте компоненты путем подачи входов и наблюдения выходов. Даже такая простая валидация может указать на немедленные способы улучшить модель. Этот пример подтверждает следующее поведение:
Когда сила прикладывается непрерывно к колесу, скорость увеличивается, пока она не достигает установившейся скорости.
Когда колеса поворачиваются в противоположных направлениях, угол поворота увеличивается с постоянной скоростью.
Создайте и запустите экспериментальную модель для компонента колеса:
Создайте новую модель. На вкладке Simulation нажмите New.
Скопируйте ![]() блок Правое колесо в новую модель.
блок Правое колесо в новую модель.
Создайте тестовое воздействие. Добавьте блок Step из библиотеки Sources и соедините его с входом блока Правое Колесо. Оставьте время шага набора параметров, чтобы 1.
Добавьте средство просмотра к выходам. Щелкните правой кнопкой мыши порт выхода блока «Правое колесо» и выберите Create & Connect Viewer > Simulink > Scope.
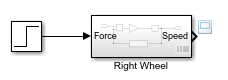
Запустите симуляцию. На вкладке Simulation нажмите Run.
![]()
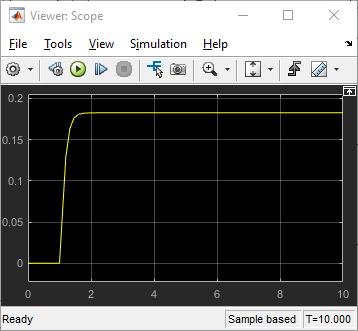
Этот результат симуляции показывает общее ожидаемое поведение. Нет движения, пока сила не приложена во время шага. Когда прикладывается сила, скорость начинает увеличиваться и затем оседает с константой, когда приложенная сила и сила сопротивления достигают равновесия. В дополнение к валидации эта симуляция также дает информацию о максимальной скорости колеса для заданной силы.
Создайте и запустите экспериментальную модель для модели вращения:
Создайте новую модель. Щелкните![]() и скопируйте блок Вращение в новую модель.
и скопируйте блок Вращение в новую модель.
Создайте тестовое воздействие в новой модели. Добавьте блок Step из библиотеки Sources. Оставьте время шага набора параметров, чтобы 1. Соедините его с входом блока Rotation. Этот вход представляет различие скоростей колеса, когда колеса вращаются в противоположных направлениях.
Добавьте средство просмотра к выходам. Щелкните правой кнопкой мыши выхода порт блока Вращение (Rotation) и выберите Create & Connect Viewer > Simulink > Scope.

Запустите симуляцию. На вкладке Simulation нажмите Run.
![]()
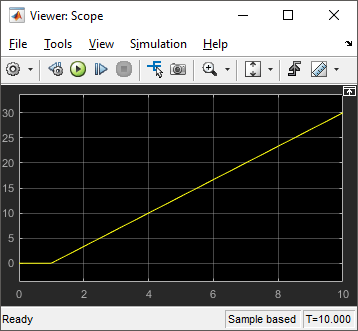
Эта симуляция показывает, что угол постоянно увеличивается, когда колеса вращаются с той же скоростью в противоположных направлениях. Можно сделать некоторые улучшения модели, чтобы легче интерпретировать выход угла, например:
Можно преобразовать выход в радианах в степени. Добавьте блок Gain с усилением 180/pi.
Можно отобразить степени выхода в циклах 360 степеней. Добавьте Math Function блок с функцией mod.
Тригонометрические функции MATLAB берут входы в радианах.
После проверки отдельных компонентов можно выполнить схожую валидацию на полной модели. В этом примере проверяется следующее поведение:
Когда к обоим колесам прикладывается одно и то же усилие в одном направлении, робот перемещается линией.
Когда к обоим колесам прикладывается одинаковая сила в противоположных направлениях, робот вращается на месте.
В system_layout дважды кликните подсистему Inputs, чтобы отобразить пустую подсистему.
Создайте тестовое воздействие путем добавления блока Step. Оставьте время шага набора параметров, чтобы 1. Соедините его с обоими блоками Outport.
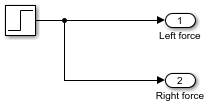
На верхнем уровне модели соедините оба выходных сигнала с одним и тем же средством просмотра возможностей:
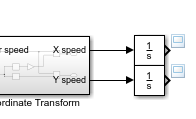
Запустите модель.
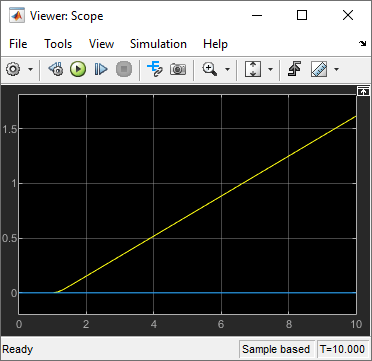
На этом рисунке желтая линия является направлением X, а синяя - направлением Y. Поскольку угол равен нулю и не меняется, транспортное средство двигается только в направлении X, как и ожидалось.
Дважды кликните Подсистему Входов и добавьте Gain с параметром -1 между источником и вторым выходом. Это меняет направление левого колеса на противоположное.
Добавьте возможности к выходу угла.
Запустите модель.
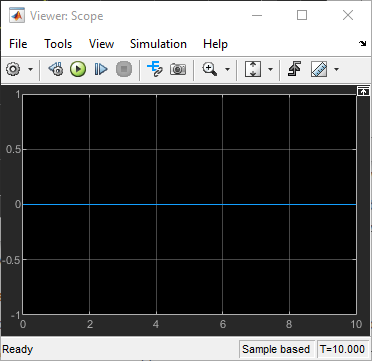
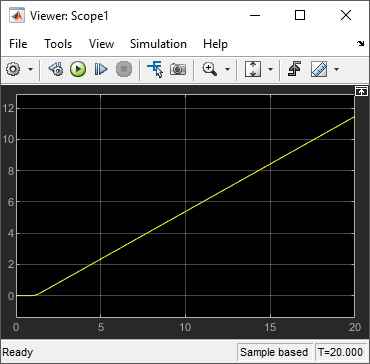
Первый вид показывает, что в плоскости X-Y нет движения. Второй вид показывает, что происходит устойчивое вращение.
Можно использовать эту окончательную модель, чтобы ответить на многие вопросы о модели путем изменения входов. Некоторые примеры:
Что происходит, когда начальный угол не равен нулю?
Сколько времени требуется для остановки движения, когда сила падает до нуля?
Что происходит, когда робот тяжелее?
Что происходит, когда робот перемещается по более гладкой поверхности, то есть когда коэффициент сопротивления ниже?