Projection

Возмущает решение решателя состояний системы, чтобы лучше удовлетворить инвариантным по времени отношениям решения

Необходимый

Нет

Язык

MATLAB

Синтаксис

Projection(s)

Аргументы

s: Образец Simulink.MSFcnRunTimeBlock класс, представляющий Блок Level-2 MATLAB S-function.

Описание

Этот метод предназначен для использования с S-функциями, которые моделируют динамические системы, состояния которых удовлетворяют инвариантным по времени отношениям, таким как те, которые являются результатом сохранения массы или энергии или других физических законов. Simulink^® engine вызывает этот метод в каждый временной шаг после того, как решатель модели вычисляет состояния S-функции для этого временного шага. Обычно небольшие ошибки в численном решении состояний заставляют решения не удовлетворять точно инвариантам решения. Ваши Projection способ может компенсировать ошибки путем возмущения состояний так, чтобы они более точно аппроксимировали инварианты решения на текущем временном шаге. В результате численное решение более тесно придерживается идеального решения по мере прогрессирования симуляции, создавая более точную общую симуляцию системы, смоделированной вашей S-функцией.

Ваши Projection возмущения метода состояний системы должны попадать в допуски на ошибки решения, заданные моделью, в которую встроена S-функция. В противном случае возмущения могут сделать решение решателя недействительным. Это зависит от вашего Projection метод, чтобы убедиться, что возмущения соответствуют допускам ошибок, заданным моделью. Смотрите Возмущение состояний системы Использование инварианта решения для простого метода для возмущения состояний системы. В следующих статьях описываются более сложные методы возмущения, что ваш mdlProjection метод может использоваться.

C.W. Gear, «Maintaining Solution Invariants in the Numerical Solution of ODE», Journal on Scientific and Statistical Computing, Vol. 7, No. 3, July 1986.
Л.Ф. Шемпина, «Законы сохранения и численное решение ОДУ I», Компьютеры и математика с приложениями, том 12B, 1986, стр. 1287-1296.
Л. Ф. Шемпин, «Законы о сохранении и численное решение ОДУ II», Компьютеры и математика с применениями, том 38, 1999, стр. 61-72.

Пример

Возмущение состояний системы с использованием инварианта решения

Вот простой, основанный на серии Тейлора подход к возмущению состояний системы. Предположим, ваша S-функция моделирует динамическую систему, имеющую инвариант решения, $g (X, t)$ , т.е. $g$ является непрерывной, дифференцируемой функцией состояний системы, $X$ , и времени, $t$ , значение которого является постоянным со временем. Тогда

$X_{n} ≅ X_{n}^{*} + J_{n}^{T} {(J_{n} J_{n}^{T})}^{- 1} R_{n}$

где

$X_{n}$ - идеальный вектор состояния системы на текущем временном шаге решателя
$X_{n}^{*}$ - приблизительный вектор состояния, вычисленный решателем в текущем временном шаге
$J_{n}$ - якобиан инвариантной функции, вычисленный в точке в пространстве состояний, заданной аппроксимационным вектором состояния на текущем временном шаге:
$J_{n} = \frac{\partial g}{\partial X} (X_{n}^{*}, t_{n})$
$t_{n}$ - время в текущем временном шаге
$R_{n}$ - невязка ( различие) между инвариантной функцией, рассчитанная в $X_{n}$ и $X_{n}^{*}$ в текущем временном шаге:
$R_{n} = g (X_{n}, t_{n}) - g (X_{n}^{*}, t_{n})$
Примечание
Значение $g (X_{n}, t_{n})$ является тем же самым на каждом временном шаге и известен по определению.

Учитывая непрерывную, дифференцируемую инвариантную функцию для системы, которую моделирует ваша S-функция, эта формула позволяет использовать mdlProjection вашей S-функции метод для вычисления возмущения

$J_{n}^{T} {(J_{n} J_{n}^{T})}^{- 1} R_{n}$

численного решения решателя, $X_{n}^{*}$ , что более близко соответствует идеальному решению, $X_{n}$ , сохраняя решение S-функции от дрейфа от идеального решения по мере прогрессирования симуляции.

Пример MATLAB

Этот пример иллюстрирует, как метод возмущения, описанный в предыдущем разделе, может удерживать численное решение модели от дрейфа от идеального решения по мере прогрессирования симуляции. Примите во внимание следующую модель, mdlProjectionEx1:

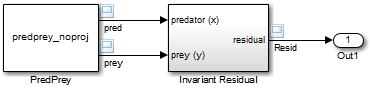
Блок PredPrey ссылается на S-функцию, predprey_noproj.m, который использует уравнения Лоток-Вольтерра

$\begin{array}{l} \dot{x} = a x (1 - y) \\ \dot{y} = - c y (1 - x) \end{array}$

для моделирования динамики популяции хищник-добыча, где $x (t)$ - плотность населения хищников и $y (t)$ - население добычи. Идеальное решение ОДУ хищника-добычи удовлетворяет инвариантной по времени функции

$x^{- c} e^{c x} y^{- a} e^{a y} = d$

где $a$ , $c$ , и $d$ являются постоянными. S-функция принимает a = 1, c = 2, и d = 121.85.

Инвариантный Остаточный блок в этой модели вычисляет невязку между инвариантной функцией, оцененной вдоль идеальной траектории системы через пространство состояний и ее моделируемой траекторией:

$R_{n} = d - x_{n}^{- c} e^{c x_{n}} y_{n}^{- a} e^{a y_{n}}$

где $x_{n}$ и $y_{n}$ являются значениями, вычисленными решателем модели для плотностей хищника и популяции жертв, соответственно, на текущем временном шаге. В идеале невязка должна быть нулем на протяжении всей симуляции модели, но симуляция модели показывает, что невязка на самом деле значительно отстает от нуля:

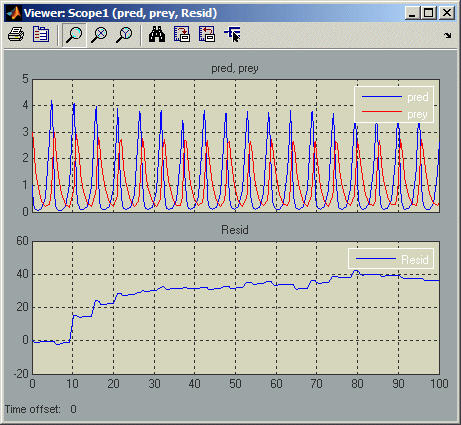
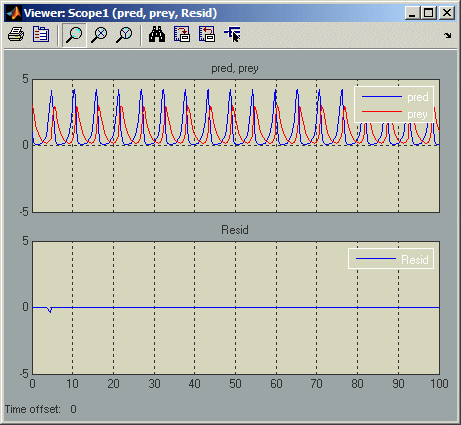
Теперь рассмотрим следующую модель, mdlProjectionEx2:

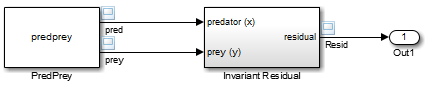
Эта модель является такой же, как и предыдущая модель, за исключением того, что ее S-функция, predprey.m, включает в себя mdlProjection метод, который использует подход возмущения, изложенный в состояниях системы возмущения, используя инвариант решения для компенсации численного дрейфа. В результате численное решение более тесно отслеживает идеальное решение по мере прогрессирования симуляции, как продемонстрировано остаточным сигналом, который остается около или в нуле на протяжении всей симуляции:

См. также

Simulink.MSFcnRunTimeBlock, mdlProjection,

Введенный в R2012b

Документация