Концепции в этой теме обеспечивают последовательный и общий язык для использования Simulink® программные инструменты.
A system является группой взаимозависимых физических и функциональных частей с измеримыми характеристиками, которые изменяются с течением времени.
Для примера транспортного средства является системой с несколькими деталями. Измеряемые характеристики включают линейную скорость транспортного средства и скорость вращения колес.
system component является частью системы, которая взаимодействует с другими частями системы. Взаимодействия между компонентами определяют структуру и поведение системы.
Для примера модуль круиз-контроля является системным компонентом в транспортное средство системе. Микроконтроллер и связанное с ним оборудование определяют структуру, в то время как программный алгоритм для управления скоростью определяет поведение.

model является математическим описанием системы, полученной либо из физических законов, либо из экспериментальных данных. Описание обычно использует набор переменных с набором дифференциальных и разностных уравнений, которые определяют отношения между переменными.
В следующем примере для транспортного средства u(t) - сила (N), перемещающая транспортное средство вперед, v(t) - скорость (м/с), b является коэффициентом перетаскивания (Nׂׂ·s/m) и m - масса транспортного средства (кг).
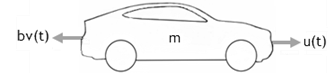
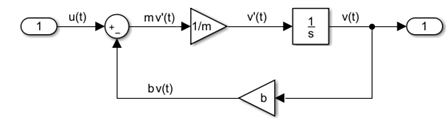
Транспортное средство является непрерывной системой. Для непрерывных систем дифференциальные уравнения описывают скорость изменения для переменных с уравнениями, заданными для всех значений времени. Скорость транспортного средства v(t)и его ускорение v'(t) заданы следующим дифференциальным уравнением первого порядка.
![]()
mv'(t) + bv(t) = u(t)
Можно создать модель Simulink для этого уравнения путем добавления блоков, определения поведения блоков и использования сигнальных линий, чтобы соединить блоки друг с другом. Следующая block diagram Simulink реализует дифференциальное уравнение.
model component является частью модели, которая взаимодействует с другими частями через интерфейс входов и выходов. Simulink реализует компоненты модели, используя Subsystem и Model блоки. Блок Model ссылается на другую модель Simulink, сохраненную в отдельном файле.
В следующем примере модель управления была сохранена в файле модели Simulink control_model.slx, а затем ссылка из блока Model во второй модели Simulink. Для моделирования механики транспортного средства был добавлен Subsystem блок.
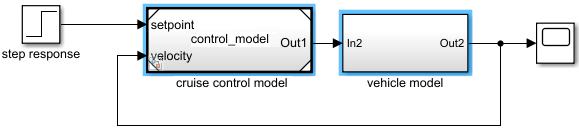
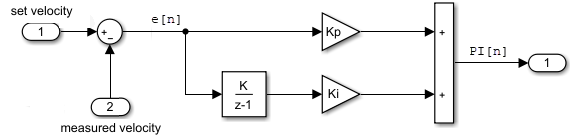
Обычно контроллеры строятся с дискретными системами, используя компьютер для реализации алгоритма управления. Для дискретных систем разностные уравнения описывают скорость изменения для переменных, заданных только в определенные моменты времени. Для примера управляющий сигнал для простой дискретной ПИ- контроллер (пропорционально-интегральный) может быть задан следующим разностным уравнением.
![]()
PI[n] = e[n]Kp + (e[n]+integral[n-1])Ki
Где e[n] - ошибка между сигналом, значение которого управляется (скорость) и заданным значением (заданная скорость), Kp - пропорциональная константа, Ki является интеграционной константой, и n - временной шаг.
Следующая Диаграмма Simulink реализует разностное уравнение.
Смотрите также: Моделируйте непрерывную систему, Основанные на компонентах Руководства по моделированию, Создайте Пользовательскую Библиотеку Модели-ссылки Основы.
Некоторые системы уравнений содержат дополнительные ограничения, которые включают независимую переменную и вектор состояния в дополнение к дифференциальным уравнениям. Такие системы называются differential algebraic equations (DAEs),
Термин algebraic относится к уравнениям, которые не включают никаких производных.
В моделях Simulink алгебраические циклы являются алгебраическими ограничениями. Модели с алгебраическими циклами задают систему дифференциальных алгебраических уравнений.
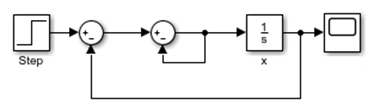
Для примера,
x' = x
0 = - x + u - 2 x
- система дифференциальных алгебраических уравнений, реализованная в следующей модели Simulink