Fixed-step solvers решите модель в регулярных временных интервалах от начала до конца симуляции. Размер интервала известен как размер шага. Можно задать размер шага или позволить решателю выбрать размер шага. Как правило, меньший размер шага увеличивает точность результатов, но также увеличивает время, необходимое для симуляции системы.
Дискретный решатель с фиксированным шагом вычисляет время следующего шага симуляции, добавив фиксированный размер шага к текущему времени. Точность и продолжительность получившейся симуляции зависят от размера шагов, предпринятых симуляцией: чем меньше размер шага, тем точнее результаты, но тем больше симуляции. По умолчанию Simulink® выбирает размер шага или можно выбрать размер шага самостоятельно. Если вы выбираете настройку по умолчанию auto, и если у модели есть дискретные шаги расчета, то Simulink устанавливает размер шага к основному шагу расчета модели. В противном случае, если дискретных скоростей не существует, Simulink устанавливает размер результата деления различия между временами начала и остановки симуляции на 50.
Эти решатели с непрерывным фиксированным шагом, как и дискретный решатель с фиксированным шагом, вычисляют следующее время симуляции, добавляя временной шаг с фиксированным размером к текущему времени. Для каждого из этих шагов непрерывные решатели используют численное интегрирование, чтобы вычислить значения непрерывных состояний для модели. Эти значения вычисляются с использованием непрерывных состояний на предыдущем временном шаге и производных состояний в промежуточных точках (мелких шагах) между текущим и предыдущим временным шагом.
Примечание
Simulink использует дискретный решатель с фиксированным шагом для модели, которая не содержит состояний или только дискретных состояний, даже если вы задаете решатель с непрерывным фиксированным шагом для модели.
Simulink предоставляет два типа решателей с непрерывным фиксированным шагом - явный и неявный.
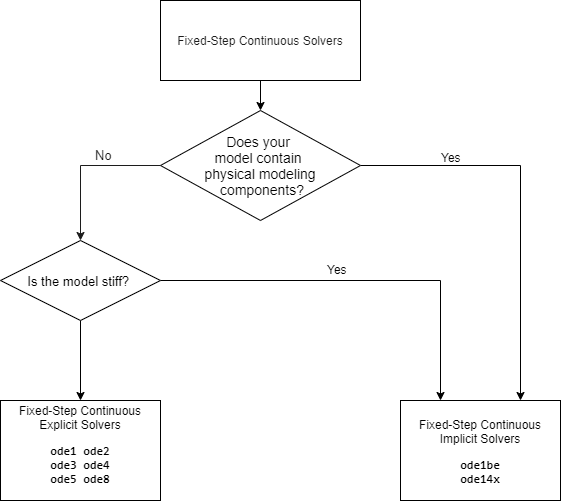
Различие между этими двумя типами заключается в скорости и стабильности. Неявный решатель требует больше расчеты на шаг, чем явный решатель, но является более стабильным. Поэтому неявный решатель с фиксированным шагом, который предоставляет Simulink, более опытен в решении жесткой системы, чем явные решатели с фиксированным шагом. Сравнение явных и неявных решателей смотрите в Явные и неявные Непрерывные решатели.
Явные решатели вычисляют значение состояния на следующем временном шаге как явную функцию от текущих значений как состояния, так и производной состояния. Явный решатель с фиксированным шагом выражается математически как:
где
x - состояние.
Dx является зависимой от решателя функцией, которая оценивает производную состояния.
h - размер шага.
n указывает текущий временной шаг.
Simulink предоставляет набор непрерывных явных решателей с фиксированным шагом. Решатели отличаются определенным методом численного интегрирования, который они используют для вычисления производных состояний модели. В этой таблице перечислены каждый решатель и метод интегрирования, который он использует. В таблице перечислены решатели в порядке вычислительной сложности используемых ими методов интегрирования, из наименее сложных (ode1) до самых сложных (ode8).
| Решатель | Метод интегрирования | Порядок точности |
|---|---|---|
| Метод Эйлера | Сначала |
| Метод Хёна | Второй |
| Формула Богацки-Шампине | Треть |
| Формула Рунге-Кутта (RK4) четвертого порядка | Четвертый |
| Формула Дорманда-Принса (RK5) | Пятый |
| Формула Дорманда-Принса RK8 (7) | Восьмой |
Ни один из этих решателей не имеет механизма управления ошибками. Поэтому точность и длительность симуляции напрямую зависят от размера шагов, предпринятых решателем. Когда вы уменьшаете размер шага, результаты становятся более точными, но симуляция занимает больше времени. Кроме того, для любого заданного размера шага, чем выше порядок решателя, тем точнее результаты симуляции.
Если вы задаете тип решателя с фиксированным шагом для модели, то по умолчанию Simulink выбирает FixedStepAuto решатель. Затем автоматический решатель выбирает соответствующий решатель с фиксированным шагом, который может обрабатывать как непрерывные, так и дискретные состояния с умеренными вычислительными усилиями. Как и в случае с дискретным решателем, если модель имеет дискретные скорости (шаги расчета), то Simulink по умолчанию устанавливает размер шага к основному времени расчета модели. Если модель не имеет дискретных скоростей, Simulink автоматически использует результат деления общей длительности симуляции на 50. Следовательно, решатель делает шаг в каждое время симуляции, в котором Simulink должен обновить дискретные состояния модели с заданными скоростями дискретизации. Однако это не гарантирует, что решатель по умолчанию точно вычисляет непрерывные состояния модели. Поэтому вам может потребоваться выбрать другой решатель, другой фиксированный размер шага или и то, и другое, чтобы достичь приемлемой точности и приемлемого времени симуляции.
Неявный решатель вычисляет состояние на следующем временном шаге как неявную функцию состояния на текущем временном шаге и производную состояния на следующем временном шаге, как описано следующим выражением.
Simulink предоставляет один неявный решатель с фиксированным шагом: ode14x. Этот решатель использует комбинацию метода Ньютона и экстраполяции из текущего значения, чтобы вычислить значение состояния на следующем временном шаге. Можно задать количество итераций метода Ньютона и порядок экстраполяции, который решатель использует для вычисления следующего значения состояния модели. См. Фиксированный размер шага (основной шаг расчета). Чем больше итераций и тем выше порядок экстраполяции, который вы выбираете, тем больше точность вы получаете. Однако вы одновременно создаете большую вычислительную нагрузку на каждый размер шага.
Выберите решатель с фиксированным шагом