Динамическая система моделируется путем вычисления ее состояний в последовательных временных шагах в течение заданного временного интервала с использованием информации, предоставленной моделью. Процесс вычисления последовательных состояний системы из ее модели известен как решение модели. Ни одного метода решения модели не хватает для всех систем. Соответственно, Simulink® предоставляет набор программ, известных как решатели, каждая из которых воплощает в себе конкретный подход к решению модели. Диалоговое окно Параметры конфигурации (Configuration Parameters) позволяет вам выбрать решатель, наиболее подходящий для вашей модели.
Вы можете выбрать решатели, предоставленные Simulink, исходя из того, как они вычисляют размер шага: fixed-step и variable-step.
Решатели с фиксированным шагом решают модель с регулярными временными интервалами от начала до конца симуляции. Размер интервала известен как размер шага. Можно задать размер шага или позволить решателю выбрать размер шага. Как правило, уменьшение размера шага увеличивает точность результатов при увеличении времени, необходимого для симуляции системы.
Решатели с переменным шагом изменяют размер шага во время симуляции. Они уменьшают размер шага, чтобы увеличить точность, когда состояния модели изменяются быстро, и увеличивают размер шага, чтобы избежать ненужных шагов, когда состояния модели изменяются медленно. Вычисление размера шага добавляет вычислительные накладные расходы на каждом шаге, но может уменьшить общее количество шагов и, следовательно, время симуляции, необходимое для поддержания заданного уровня точности для моделей с быстро изменяющимися или кусочно-непрерывными состояниями.
Решатели с фиксированным шагом и переменным шагом вычисляют следующее время симуляции как сумму текущего времени симуляции и размера шага. Управление Type на панели строения Solver позволяет вам выбрать тип решателя. С помощью решателя с фиксированным шагом размер шага остается постоянным на протяжении всей симуляции. С помощью решателя с переменным шагом размер шага может варьироваться от шага к шагу, в зависимости от динамики модели. В частности, решатель с переменным шагом увеличивает или уменьшает размер шага, чтобы соответствовать допускам ошибки, которые вы задаете.
Выбор между этими типами зависит от того, как вы планируете развертывать модель и динамику модели. Если вы планируете сгенерировать код из вашей модели и запустить код на компьютерной системе реального времени, выберите решатель с фиксированным шагом, чтобы симулировать модель. Вы не можете сопоставить размер шага переменной с временем в реальном времени.
Если вы не планируете развертывать модель в качестве сгенерированного кода, выбор между переменным шагом и решателем с фиксированным шагом зависит от динамики вашей модели. Решатель с переменным шагом может значительно сократить время симуляции вашей модели. Решатель с переменным шагом позволяет эту сохранение, потому что для заданного уровня точности решатель может динамически регулировать размер шага по мере необходимости. Этот подход сокращает количество необходимых шагов. Решатель с фиксированным шагом должен использовать один размер шага на протяжении всей симуляции, основанный на требованиях точности. Чтобы удовлетворить эти требования на протяжении всей симуляции, решатель с фиксированным шагом обычно требует небольшого шага.
The ex_multirate пример модели показывает, как решатель с переменным шагом может сократить время симуляции для многоразовой дискретной модели.
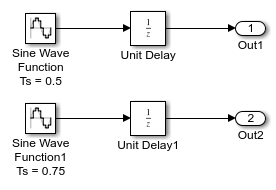
Модель генерирует выходы с двумя различными скоростями: каждые 0,5 с и каждые 0,75 с. Чтобы захватить оба выходов, решатель с фиксированным шагом должен делать временной шаг каждые 0,25 с (основной шаг расчета для модели).
[0.0 0.25 0.5 0.75 1.0 1.25 1.5 ...]
В отличие от этого, решатель с переменным шагом должен делать шаг только, когда модель генерирует выход.
[0.0 0.5 0.75 1.0 1.5 ...]
Эта схема значительно сокращает количество временных шагов, необходимых для симуляции модели.
Simulink предоставляет как непрерывные, так и дискретные решатели.
Когда вы выбираете тип решателя, вы также можете выбрать конкретный решатель. Оба набора решателей включают дискретные и непрерывные решатели. Дискретные и непрерывные решатели полагаются на блоки модели, чтобы вычислить значения любых дискретных состояний. Блоки, которые задают дискретные состояния, отвечают за вычисление значений этих состояний на каждом временном шаге. Однако, в отличие от дискретных решателей, непрерывные решатели используют численное интегрирование, чтобы вычислить непрерывные состояния, которые задают блоки. При выборе решателя сначала определите, использовать ли дискретный решатель или непрерывный решатель.
Если ваша модель не имеет непрерывных состояний, то Simulink переключается либо на дискретный решатель с фиксированным шагом, либо на дискретный решатель с переменным шагом. Если ваша модель имеет только непрерывные состояния или смесь непрерывных и дискретных состояний, выберите непрерывный решатель из остальных вариантов решателя на основе динамики вашей модели. В противном случае возникает ошибка.
Continuous решатели используют численное интегрирование, чтобы вычислить непрерывные состояния модели в текущем временном шаге на основе состояний на предыдущих временных шагах и производных состояний. Непрерывные решатели полагаются на отдельные блоки, чтобы вычислить значения дискретных состояний модели на каждом временном шаге.
Дискретные решатели существуют в первую очередь для решения чисто дискретных моделей. Они вычисляют следующий временной шаг симуляции для модели и ничего другого. При выполнении этих расчетов они полагаются на каждый блок в модели, чтобы обновить его отдельные дискретные состояния. Они не вычисляют непрерывные состояния.
Библиотека решателя содержит два дискретных решателя: дискретный решатель с фиксированным шагом и дискретный решатель с переменным шагом. Решатель с фиксированным шагом по умолчанию выбирает размер шага и скорость симуляции достаточно быстро, чтобы отслеживать изменения состояния в самом быстром блоке вашей модели. Решатель с переменным шагом корректирует размер шага симуляции, чтобы идти в ногу с фактической частотой дискретных изменений состояния в вашей модели. Эта корректировка может избежать ненужных шагов и сократить время симуляции для многоскоростных моделей. Смотрите Шаги расчета в системах для получения дополнительной информации.
Примечание
Вы должны использовать непрерывный решатель, чтобы решить модель, которая содержит как непрерывные, так и дискретные состояния, потому что дискретные решатели не могут обрабатывать непрерывные состояния. Если, с другой стороны, вы выбираете непрерывный решатель для модели без состояний или только дискретных состояний, программа Simulink использует дискретный решатель.
Вы представляете явную систему уравнением
Для любого заданного значения x можно вычислить путем подстановки x в f(x) и оценки уравнения.
Уравнения вида
считаются неявными. Для любого заданного значения , вы должны решить это уравнение, чтобы вычислить .
Линейно неявная система может быть представлена уравнением
M (x) называется большой матрицей - принудительная функция. Система становится линейно неявной, когда вы используете блоки физического моделирования в модели.
В то время как вы можете применить неявный или явный непрерывный решатель, для решения этих систем, неявные решатели специально разработаны для того, чтобы решить жесткие задачи. Явные решатели решают нежесткие задачи. Задача обыкновенного дифференциального уравнения, называется жесткой, если требуемое решение изменяется медленно, но существуют более близкие решения, которые изменяются быстро. В таком случае численный метод должен взять небольшие временные шаги, чтобы решить систему. Жесткость является проблемой эффективности. Чем более жесткая система, тем больше времени требуется явному решателю для выполнения расчетов. Жесткая система имеет как медленно, так и быстро непрерывно изменяющуюся динамику.
При сравнении с явными решателями неявные решатели обеспечивают большую стабильность для колебательного поведения. Однако неявные решатели также в вычислительном отношении дороже. Они генерируют матрицу Якобия и решают набор алгебраических уравнений на каждом временном шаге с помощью ньютоноподобного метода. Чтобы уменьшить эту дополнительную стоимость, неявные решатели предлагают параметр Solver Jacobian method, который позволяет улучшить эффективность симуляции неявных решателей. Дополнительные сведения см. в разделе Выбор якобианского метода для неявного решателя. Неявные решатели более эффективны, чем явные решатели для решения линейно неявной системы.
Библиотека решателей Simulink обеспечивает как одношаговый, так и многоступенчатый решатели. Одношаговые решатели оценивают![]() с помощью решения в непосредственно предшествующий момент времени
с помощью решения в непосредственно предшествующий момент времени ![]() и значения производной в нескольких точках между tn и tn-1. Эти точки являются мелкими шагами.
и значения производной в нескольких точках между tn и tn-1. Эти точки являются мелкими шагами.
Мультистеповые решатели используют результаты в нескольких предыдущих временных шагах, чтобы вычислить текущее решение. Simulink предоставляет один явный многоступенчатый решатель, ode113и один неявный многостадийный решатель, ode15s. Оба являются решателями с переменным шагом.
Это различие основано на количестве порядков, которые решатель использует для решения системы уравнений. Два решателя переменного порядка, ode15s и ode113, являются частью библиотеки решателя. Они используют несколько порядков, чтобы решить систему уравнений. В частности, неявный, переменный-шаг ode15s решатель использует уравнения первого-пятого порядка, в то время как явный, переменный-шаг ode113 решатель использует уравнения первого - тринадцатого порядков. Для ode15sможно ограничить наивысший порядок, применяемый параметром Maximum Order. Для получения дополнительной информации смотрите Максимальный порядок.
Фазы симуляции в динамических системах | Модели Simulink | Обнаружение пересечения нулем