Документация

Чисто дискретные системы

Чисто дискретная система состоит исключительно из дискретных блоков и может быть смоделирована с помощью либо решателя с фиксированным шагом, либо решателя с переменным шагом. Симуляция дискретной системы требует, чтобы симулятор делал шаг симуляции при каждом шаге расчета. Для многократной дискретной системы - системы, блоки которой Simulink^® выборки с различными скоростями - шаги должны происходить с целым числом, кратным каждому из системных шагов расчета. В противном случае симулятор может пропустить ключевые переходы в состояниях системы. Размер шага, который выбирает программное обеспечение Simulink, зависит от типа решателя, который вы используете для симуляции многоразовой системы, и от основного шага расчета.

Основной шаг расчета многоразовой дискретной системы является самым большим двойником, который является целочисленным делителем фактических шагов расчета системы. Например, предположим, что система имеет шаги расчета 0,25 и 0,50 секунд. Основной шаг расчета в этом случае составляет 0,25 секунды. Предположим, вместо этого, шаги расчета составляют 0,50 и 0,75 секунды. Основной шаг расчета снова составляет 0,25 секунд.

Важность основного шага расчета непосредственно связана с тем, направляете ли вы программное обеспечение Simulink на использование дискретного решателя с фиксированным шагом или с переменным шагом, чтобы решить вашу многоразовую дискретную систему. Решатель с фиксированным шагом устанавливает размер шага симуляции равным основному шагу расчета дискретной системы. Напротив, решатель с переменным шагом изменяет размер шага, чтобы равняться расстоянию между фактическими попаданиями шаг расчета.

Следующая схема иллюстрирует различие между решателем с фиксированным шагом и решателем с переменным шагом.

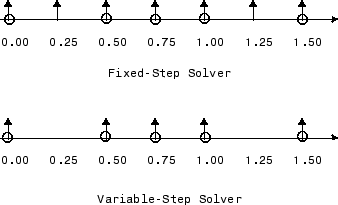
В схеме стрел указывают шаги симуляции, а круги представляют шагу расчета попадания. Как иллюстрирует схема, решатель с переменным шагом требует меньшего количества шагов симуляции, чтобы симулировать систему, если основное время расчета меньше, чем любое из фактических шагов расчета моделируемой системы. С другой стороны, решатель с фиксированным шагом требует меньше памяти для реализации и быстрее, если одно из системных шагов расчета является фундаментальным. Это может быть преимуществом в приложениях, которые влекут за собой генерацию кода из модели Simulink (использование Simulink Coder™). В любом случае дискретный решатель, предоставляемый Simulink, оптимизирован для дискретных систем; однако можно симулировать чисто дискретную систему с любым из решателей и получить эквивалентные результаты.

Рассмотрим следующий пример простой многократной системы. В данном примере DTF1 Discrete Transfer Fcn блок Шаг расчета устанавливается на [1 0.1] [], что дает ему смещение 0.1. Для Шага расчета блока DTF2 Discrete Transfer Fcn задано значение 0.7 , без смещения. Решатель устанавливается на дискретный решатель с переменным шагом.

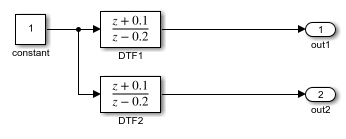
Выполнение симуляции и построение графика выходов с помощью stairs функция

set_param(bdroot,'SolverType','Variable-Step','SolverName','VariableStepDiscrete','SaveFormat','Array');
simOut = sim(bdroot,'Stoptime','3');
stairs(simOut.tout,simOut.yout,'-*','LineWidth',1.2);
xlabel('Time (t)');
ylabel('Outputs (out1,out2)');
legend('t_s = [1, 0.1]','t_s = 0.7','location','best')

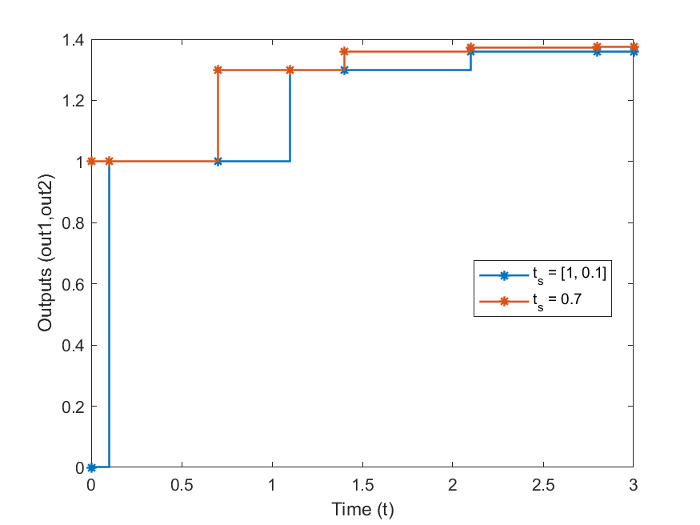
создает следующий график.

(Для получения информации о sim команда. см. «Запуск симуляций программно».)

Как показано на рисунке, потому что блок DTF1 имеет 0.1 смещение, блок DTF1 не имеет выхода, пока t = 0.1. Точно так же начальные условия передаточных функций равны нулю; поэтому выход DTF1 y (1) равен нулю перед этим временем.

Гибридные системы

Гибридные системы содержат как дискретные, так и непрерывные блоки и, таким образом, имеют как дискретные, так и непрерывные состояния. Однако решатели Simulink рассматривают любую систему, которая имеет как непрерывные так и дискретные шаги расчета, как гибридную систему. Для получения информации о моделировании гибридных систем смотрите Моделирование гибридных систем.

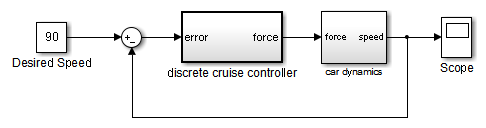
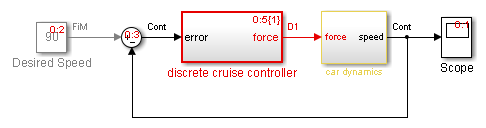
В блоках термин гибрид применяется как к гибридным системам (смешанные непрерывно-дискретные системы), так и к системам с несколькими шагами расчета (мультирейт-системы). Такие системы становятся желтыми в цвете, когда вы выполняете Update Diagram с Colors Sample Time Display 'on'. В качестве примера рассмотрим следующую модель, которая содержит атомарную подсистему «Discrete Cruise Controller» и виртуальную подсистему «Car Dynamics». (См. ex_execution_order.)

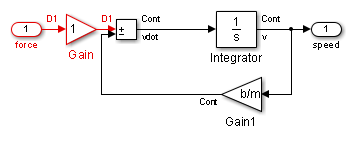
С опцией Sample Time, установленной на All, Update Diagram поворачивает виртуальную подсистему желтым цветом, указывая, что она является гибридной подсистемой. В этом случае подсистема является истинной гибридной системой, поскольку она имеет как непрерывные так и дискретные шаги расчета. Как показано ниже, дискретный входной сигнал D1 объединяется с сигналом непрерывной скорости v, чтобы создать непрерывный вход для интегратора.

Теперь рассмотрим многоразовую подсистему, которая содержит три Sine Wave исходные блоки, каждая из которых имеет уникальный шаг расчета - 0,2, 0,3 и 0,4 соответственно.

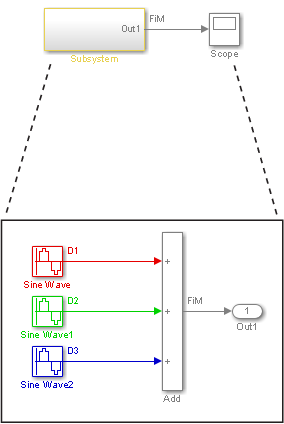
Update Diagram поворачивает подсистему, желтую, потому что подсистема содержит больше чем в один раз. Как показано на блок-схеме, блоки Sine Wave имеют дискретные шаги расчета D1, D2 и D3, и выходной сигнал фиксируется на мелком шаге.

При оценке системы для нескольких шагов расчета Simulink не рассматривает ни постоянные [inf, 0], ни асинхронные [-1, -n] шаги расчета. Таким образом, подсистема, состоящая из одного блока, который выводит постоянное значение, и одного блока с дискретным шагом расчета, не будет обозначена как гибридная.

Гибридная аннотация и раскраска очень полезны для оценки того, унаследовали ли подсистемы в вашей модели правильное или ожидаемые шаги расчета.