Модели смешанных эффектов

Введение в модели смешанных эффектов

В статистике effect является всем, что влияет на значение переменной отклика в конкретной настройке переменных предиктора. Эффекты переводятся в параметры модели. В линейных моделях эффекты становятся коэффициентами, представляющими пропорциональные вклады модельных членов. В нелинейных моделях эффекты часто имеют специфические физические интерпретации и появляются в более общих нелинейных комбинациях.

Fixed effects представлять параметры населения, приняты одинаковыми каждый раз, когда данные собираются. Оценка фиксированных эффектов является традиционной областью регрессионного моделирования. Random effects, для сравнения, являются зависимыми от выборки случайными переменными. В моделировании случайные эффекты действуют как дополнительные условия ошибки, и их распределения и ковариации должны быть заданы.

Например, рассмотрим модель элиминации препарата из кровотока. Модель использует t времени в качестве предиктора и концентрацию лекарственного C в качестве ответа. Нелинейный модельный термин C 0 e^–rt объединяет параметры C 0 и r, представляющие, соответственно, начальную концентрацию и скорость удаления. Если данные собираются через несколько индивидуумов, разумно предположить, что скорость исключения является случайной переменной _r i зависящей от индивидуума i, варьирующейся вокруг среднего совокупности $\bar{r}$ . Термин C 0 e^–rt становится

$C_{0} e^{- [\bar{r} + (r_{i} - \bar{r})] t} = C_{0} e^{- (β + b_{i}) t},$

где β = $\bar{r}$ является фиксированным эффектом и b i = $r_{i} - \bar{r}$ является случайным эффектом.

Случайные эффекты применяются, когда данные попадают в естественные группы. В модели элиминации лекарств группами являются просто исследуемые люди. Более сложные модели могут сгруппировать данные по индивидууму возрасту, весу, диете и т. Д. Хотя группы не являются особым вниманием исследования, добавление случайных эффектов в модель расширяет достоверность выводов за пределы конкретной выборки индивидуумов.

Mixed-effects models учитывают как фиксированные, так и случайные эффекты. Как и во всех регрессионных моделях, их цель состоит в том, чтобы описать переменную отклика как функцию от переменных предиктора. Модели со смешанными эффектами, однако, распознают корреляции в выборочных подгруппах. Таким образом, они обеспечивают компромисс между игнорированием групп данных полностью и подбором кривой каждой группы к отдельной модели.

Иерархия модели смешанных эффектов

Предположим, что данные для нелинейной регрессионой модели попадают в одну из m разных групп i = 1,..., m. Чтобы принять во внимание группы в модели, запишите j отклика в i групп как:

$y_{i j} = f (φ, x_{i j}) + ε_{i j}$

<reservedrangesplaceholder22> <reservedrangesplaceholder21> <reservedrangesplaceholder20> - ответ, <reservedrangesplaceholder19> <reservedrangesplaceholder18> <reservedrangesplaceholder17> вектор предсказателей, φ - вектор параметров модели, и <reservedrangesplaceholder15> <reservedrangesplaceholder14> <reservedrangesplaceholder13> - ошибка процесса или измерение. Индекс j в диапазоне от 1 до n i, где n i - количество наблюдений в группе i. Функция f задает форму модели. Часто, <reservedrangesplaceholder5> <reservedrangesplaceholder4> <reservedrangesplaceholder3> - просто время <reservedrangesplaceholder2> <reservedrangesplaceholder1> <reservedrangesplaceholder0> наблюдения. Ошибки обычно принимаются независимыми и идентичными, обычно распределенными, с постоянным отклонением.

Оценки параметров в φ описывают население, принимая, что эти оценки одинаковы для всех групп. Если, однако, оценки варьируются по группам, модель становится

$y_{i j} = f (φ_{i}, x_{i j}) + ε_{i j}$

В модели со смешанными эффектами φ i может быть комбинацией фиксированного и случайного эффектов:

$φ_{i} = β + b_{i}$

Случайные эффекты b i обычно описываются как многомерные, нормально распределенные, со средним нулями и ковариацией Оценивая фиксированные эффекты β и ковариация случайных эффектов Ψ предоставляет описание населения, которое не предполагает, что параметры <reservedrangesplaceholder3> <reservedrangesplaceholder2> - то же через группы. Оценка случайных эффектов b i также дает описание конкретных групп в данных.

Параметры модели не должны идентифицироваться с отдельными эффектами. В целом design matrices A и B используются для идентификации параметров с линейными комбинациями фиксированных и случайных эффектов:

$φ_{i} = A β + B b_{i}$

Если матрицы проекта различаются среди групп, модель становится

$φ_{i} = A_{i} β + B_{i} b_{i}$

Если матрицы проекта также различаются среди наблюдений, модель становится

$\begin{array}{l} φ_{i j} = A_{i j} β + B_{i j} b_{i} \\ y_{i j} = f (φ_{i j}, x_{i j}) + ε_{i j} \end{array}$

Некоторые предикторы группы в x _i j могут не измениться с j наблюдения. Вызывая эти v i, модель становится

$y_{i j} = f (φ_{i j}, x_{i j}, v_{i}) + ε_{i j}$

Определение моделей смешанных эффектов

Предположим, что данные для нелинейной регрессионой модели попадают в одну из m разных групп i = 1,..., m. (В частности, предположим, что группы не вложены.) Чтобы задать общую нелинейную модель смешанных эффектов для этих данных:

Задайте групповые параметры модели φ i как линейные комбинации фиксированных эффектов β и случайных эффектов _b i.
Определите значения отклика <reservedrangesplaceholder4> <reservedrangesplaceholder3> как нелинейную функцию f параметров и определенных для группы переменных <reservedrangesplaceholder1> <reservedrangesplaceholder0> предсказателя.

Модель является:

$\begin{array}{l} φ_{i} = A_{i} β + B_{i} b_{i} \\ y_{i} = f (φ_{i}, X_{i}) + ε_{i} \\ b_{i} \sim N (0, Ψ) \\ ε_{i} \sim N (0, σ^{2}) \end{array}$

Эта формулировка нелинейной модели смешанных эффектов использует следующее обозначение:

<reservedrangesplaceholder1> <reservedrangesplaceholder0>	Вектор параметров модели для группы
β	Вектор фиксированных эффектов, моделирование параметров населения
<reservedrangesplaceholder1> <reservedrangesplaceholder0>	Вектор многомерных обычно распределенных групповых случайных эффектов
<reservedrangesplaceholder1> <reservedrangesplaceholder0>	Групповая матрица проекта для объединения фиксированных эффектов
<reservedrangesplaceholder1> <reservedrangesplaceholder0>	Групповая матрица проекта для объединения случайных эффектов
<reservedrangesplaceholder1> <reservedrangesplaceholder0>	Матрица данных предикторных значений для группы
<reservedrangesplaceholder1> <reservedrangesplaceholder0>	Вектор данных относящихся к группе значений отклика
f	Общая, реальная функция φ i и _X i
<reservedrangesplaceholder1> <reservedrangesplaceholder0>	Вектор специфических для группы ошибок, принятый независимым, идентичным, обычно распределенным и независимым от b i
Ψ	Ковариационная матрица для случайных эффектов
σ²	Отклонение ошибок, принятая постоянной между наблюдениями

Например, рассмотрим модель элиминации препарата из кровотока. Модель включает две перекрывающиеся фазы:

Начальная фаза p во время которой концентрации лекарства достигают равновесия с окружающими тканями
Вторая фаза q во время которой лекарство удаляется из кровотока

Для данных о нескольких индивидуумах, i, модель является

$y_{i j} = C_{p i} e^{- r_{p i} t_{i j}} + C_{q i} e^{- r_{q i} t_{i j}} + ε_{i j},$

где <reservedrangesplaceholder6> <reservedrangesplaceholder5> <reservedrangesplaceholder4> - наблюдаемая концентрация в индивидууме i во время <reservedrangesplaceholder2> <reservedrangesplaceholder1> <reservedrangesplaceholder0>. Модель позволяет различное время выборки и разное количество наблюдений для разных индивидуумов.

Темпы <reservedrangesplaceholder17> <reservedrangesplaceholder16> <reservedrangesplaceholder15> устранения и <reservedrangesplaceholder14> <reservedrangesplaceholder13> <reservedrangesplaceholder12> должны быть намерены быть физически значащими. Проведите в жизнь это, введя ставки <reservedrangesplaceholder11> <reservedrangesplaceholder10> <reservedrangesplaceholder9> журнала = журнал (r <reservedrangesplaceholder7> <reservedrangesplaceholder6>) и <reservedrangesplaceholder5> <reservedrangesplaceholder4> <reservedrangesplaceholder3> = журнал (r <reservedrangesplaceholder1> <reservedrangesplaceholder0>) и повторно параметризуя модель:

$y_{i j} = C_{p i} e^{- \exp (R_{p i}) t_{i j}} + C_{q i} e^{- \exp (R_{q i}) t_{i j}} + ε_{i j}$

Выбор параметров для модели со случайными эффектами является важным фактором при построении модели смешанных эффектов. Одним из методов является добавление случайных эффектов ко всем параметрам и использование оценок их отклонений для определения их значимости в модели. Альтернативой является подгонка модели отдельно к каждой группе без случайных эффектов и просмотр изменения оценок параметров. Если оценка широко варьируется между группами или если доверительные интервалы для каждой группы имеют минимальное перекрытие, параметр является хорошим кандидатом для случайного эффекта.

Чтобы ввести фиксированные эффекты β и случайные эффекты b i для всех параметров модели, повторно экспрессируйте модель следующим образом:

$\begin{array}{l} y_{i j} & = & [{\bar{C}}_{p} + (C_{p i} - {\bar{C}}_{p})] e^{- \exp [{\bar{R}}_{p} + (R_{p i} - {\bar{R}}_{p})] t_{i j}} + \\ [{\bar{C}}_{q} + (C_{q i} - {\bar{C}}_{q})] e^{- \exp [{\bar{R}}_{q} + (R_{q i} - {\bar{R}}_{q})] t_{i j}} + ε_{i j} \\ = & (β_{1} + b_{1 i}) e^{- \exp (β_{2} + b_{2 i}) t_{i j}} + \\ (β_{3} + b_{3 i}) e^{- \exp (β_{4} + b_{4 i}) t_{i j}} + ε_{i j} \end{array}$

В обозначении общей модели:

$β = (\begin{matrix} β_{1} \\ ⋮ \\ β_{4} \end{matrix}), b_{i} = (\begin{matrix} b_{i 1} \\ ⋮ \\ b_{i 4} \end{matrix}), y_{i} = (\begin{matrix} y_{i 1} \\ ⋮ \\ y_{i n_{i}} \end{matrix}), X_{i} = (\begin{matrix} t_{i 1} \\ ⋮ \\ t_{i n_{i}} \end{matrix}),$

где n i - количество наблюдений индивидуума i. В этом случае матрицы проекта _A i и B i являются, по крайней мере, первоначально, матрицами тождеств 4 на 4. Матрицы проекта могут быть изменены, при необходимости, чтобы ввести взвешивание отдельных эффектов или временной зависимости.

Подгонка модели и оценка ковариационной матрицы Относительно небольшая оценка отклонения случайного эффекта предполагает, что она может быть удалена из модели. Аналогичным образом, относительно небольшие оценки для ковариаций среди определенных случайных эффектов предполагают, что полная ковариационная матрица ненужна. Поскольку случайные эффекты являются неограниченными, Установка диагонали или блочно-диагонального шаблона ковариации для, может улучшить сходимость и эффективность алгоритма аппроксимации.

Statistics and Machine Learning Toolbox™ nlmefit и nlmefitsa подгонка общей нелинейной модели смешанных эффектов к данным, оценка фиксированных и случайных эффектов. Функции также оценивают ковариационную матрицу Дополнительные диагностические выходы позволяют вам оценить компромиссы между количеством параметров модели и качеством подгонки.

Определение ковариатных моделей

Если модель в Определении моделей смешанных эффектов принимает зависимую от группы ковариату, такую как вес (w), модель становится:

$(\begin{matrix} φ_{1} \\ φ_{2} \\ φ_{3} \end{matrix}) = (\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \begin{matrix} w i \\ 0 \\ 0 \end{matrix}) (\begin{matrix} β_{1} \\ β_{2} \\ \begin{array}{l} β_{3} \\ β_{4} \end{array} \end{matrix}) + (\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}) (\begin{matrix} b_{1} \\ b_{2} \\ b_{3} \end{matrix})$

Таким образом, параметр φ i для любого индивидуума в ith группа является:

$(\begin{matrix} φ_{1_{i}} \\ φ_{2_{i}} \\ φ_{3_{i}} \end{matrix}) = (\begin{matrix} β_{1} + β_{4} * w_{i} \\ β_{2} \\ β_{3} \end{matrix}) + (\begin{matrix} b_{1_{i}} \\ b_{2_{i}} \\ b_{3_{i}} \end{matrix})$

Чтобы задать ковариатную модель, используйте 'FEGroupDesign' опция.

'FEGroupDesign' является p-by-q-by-m массив, задающий другое p-by-q матрица проекта с фиксированными эффектами для каждого из m группы. Используя предыдущий пример, массив напоминает следующее:

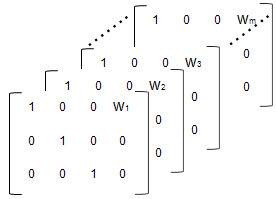
Создайте массив.

% Number of parameters in the model (Phi)
num_params = 3;
% Number of covariates
num_cov = 1;
% Assuming number of groups in the data set is 7
num_groups = 7;
% Array of covariate values
covariates = [75; 52; 66; 55; 70; 58; 62 ];
A = repmat(eye(num_params, num_params+num_cov),...
[1,1,num_groups]);
A(1,num_params+1,1:num_groups) = covariates(:,1)

Создайте struct с заданной матрицей проекта.
```
options.FEGroupDesign = A; 
```
Задайте аргументы для nlmefit (или nlmefitsa) как показано на моделях смешанных эффектов с использованием nlmefit и nlmefitsa.

Выбор `nlmefit` или `nlmefitsa`

Statistics and Machine Learning Toolbox обеспечивает две функции, nlmefit и nlmefitsa для подбора кривой нелинейных моделей смешанных эффектов. Каждая функция предоставляет различные возможности, которые могут помочь вам решить, какие из них использовать.

Методы приближения
Параметры, характерные для nlmefitsa
Требования к модели и данным

Методы приближения

nlmefit предоставляет следующие четыре метода приближения для подбора кривой нелинейных моделей смешанных эффектов:

'LME' - Используйте вероятность для модели линейных смешанных эффектов при текущих условных оценках beta и B. Это значение по умолчанию.
'RELME' - Используйте ограниченную правдоподобность для модели линейных смешанных эффектов при текущих условных оценках beta и B.
'FO' - Лаплаковское приближение первого порядка без случайных эффектов.
'FOCE' - Лаплаковское приближение первого порядка при условных оценках B.

nlmefitsa предоставляет дополнительный метод аппроксимации, Стохастическое Приближение Ожидание-Максимизация (SAEM) [25] с тремя шагами:

Симуляция: Сгенерируйте моделируемые значения случайных эффектов, b из апостериорной p плотности (b |
Стохастическое приближение: Обновите ожидаемое значение функции правдоподобия журнала, взяв ее значение от предыдущего шага и двигаясь частично к среднему значению правдоподобия журнала, рассчитанному из моделируемых случайных эффектов.
Шаг максимизации: Выберите новые оценки параметров, чтобы максимизировать журнал функцию правдоподобия, учитывая моделируемые значения случайных эффектов.

Оба nlmefit и nlmefitsa попытка найти оценки параметров для максимизации функции правдоподобия, которую трудно вычислить. nlmefit решает задачу путем аппроксимации функции правдоподобия различными способами и максимизации аппроксимационной функции. Он использует традиционные методы оптимизации, которые зависят от таких вещей, как критерии сходимости и пределы итерации.

nlmefitsaс другой стороны, моделирует случайные значения параметров таким образом, чтобы в долгосрочном запуске они сходились к значениям, которые максимизируют точную функцию правдоподобия. Результаты случайны, и традиционные тесты сходимости не применяются. Поэтому nlmefitsa предоставляет опции для построения графика результатов по мере прогрессирования симуляции и для повторного запуска симуляции несколько раз. Можно использовать эти функции, чтобы определить, сходились ли результаты к требуемой точности.

Параметры, характерные для `nlmefitsa`

Следующие параметры характерны для nlmefitsa. Большинство управляют стохастическим алгоритмом.

Cov0 - Начальное значение для ковариационной матрицы PSI. Должна быть r -by r положительно определенной матрицей. Если он пуст, значение по умолчанию зависит от значений BETA0.
ComputeStdErrors — true вычислить стандартные ошибки для оценок коэффициентов и сохранить их в выход STATS структура, или false (по умолчанию), чтобы опустить эти расчеты.
LogLikMethod - задает метод аппроксимации вероятности журнала.
NBurnIn - Количество начальных итераций горения, в течение которых оценки параметра не пересчитываются. Значение по умолчанию является 5.
NIterations - Управляет тем, сколько итераций выполняется для каждой из трех фаз алгоритма.
NMCMCIterations - Количество итераций марковской цепи Монте-Карло (MCMC).

Требования к модели и данным

Существуют некоторые различия в возможностях nlmefit и nlmefitsa. Поэтому некоторые данные и модели могут использоваться с любой функцией, но некоторые могут потребовать, чтобы вы выбрали только одну из них.

Модели ошибок - nlmefitsa поддерживает различные модели ошибок. Для примера стандартное отклонение отклика может быть постоянным, пропорциональным значению функции или комбинации двух. nlmefit подходит для моделей при условии, что стандартное отклонение отклика постоянно. Одна из моделей ошибок, 'exponential', указывает, что журнал отклика имеет постоянное стандартное отклонение. Подгонять такие модели можно используя nlmefit путем предоставления журнала отклика в качестве входного параметра и путем переписывания функции модели для получения журнала значения нелинейной функции.
Случайные эффекты - обе функции подгоняют данные к нелинейной функции с параметрами, и параметрами могут быть простые скалярные значения или линейные функции ковариат. nlmefit позволяет любым коэффициентам линейных функций иметь как фиксированные, так и случайные эффекты. nlmefitsa поддерживает случайные эффекты только для постоянного (перехват) коэффициента линейных функций, но не для коэффициентов наклона. Итак, в примере определения ковариатных моделей nlmefitsa может рассматривать только первые три значения беты как случайные эффекты.
Форма модели - nlmefit поддерживает очень общую спецификацию модели с небольшими ограничениями на матрицы проекта, которые связывают фиксированные коэффициенты и случайные эффекты с параметрами модели. nlmefitsa является более ограничительным:
- Проект фиксированного эффекта должен быть постоянным в каждой группе (для каждого индивидуума), поэтому зависящий от наблюдений проект не поддерживается.
- Конструкция случайного эффекта должна быть постоянной для всего набора данных, поэтому не поддерживается ни проект, зависящий от наблюдений, ни проект, зависящий от группы.
- Как упоминалось в разделе Случайные эффекты (Random Effects), проект случайного эффекта не должна задавать случайные эффекты для коэффициентов наклона. Это подразумевает, что проект должна состоять из нулей и таковых.
- Проект случайного эффекта не должна использовать тот же случайный эффект для нескольких коэффициентов и не может использовать больше одного случайного эффекта для любого отдельного коэффициента.
- Проект фиксированного эффекта не должен использовать один и тот же коэффициент для нескольких параметров. Это означает, что это может иметь самое большее одно ненулевое значение в каждом столбце.
Если вы хотите использовать nlmefitsa для данных, в которых ковариатные эффекты случайны, включите ковариаты непосредственно в выражение нелинейной модели. Не включать ковариаты в матрицы проекта с фиксированным или случайным эффектом.
Сходимость - как описано в форме Модель, nlmefit и nlmefitsa имеют различные подходы к измерению сходимости. nlmefit использует традиционные меры оптимизации и nlmefitsa предоставляет диагностику, которая поможет вам судить о сходимости случайной симуляции.

На практике nlmefitsa имеет тенденцию быть более устойчивым и с меньшей вероятностью не справится с трудными проблемами. Однако nlmefit может быстрее сходиться к проблемам, где он сходится вообще. Некоторые проблемы могут быть полезны от комбинированной стратегии, например, путем выполнения nlmefitsa на время, чтобы получить разумные оценки параметров и использовать их в качестве начальной точки для дополнительных итераций, используя nlmefit.

Использование выходных функций с моделями смешанных эффектов

The Outputfcn поле options структура задает одну или несколько функций, которые решатель вызовов после каждой итерации. Обычно можно использовать выходную функцию для построения графика точек при каждой итерации или для отображения оптимизационных величин из алгоритма. Чтобы настроить выходную функцию:

Запишите выходную функцию как MATLAB^® файловая функция или локальная функция.
Использование statset задать значение Outputfcn быть указателем на функцию, то есть именем функции, предшествующей @ знак. Для примера, если выходная функция outfun.m, команду
```
 options = statset('OutputFcn', @outfun);
```
задает OutputFcn быть указателем на outfun. Чтобы задать несколько выходных функций, используйте синтаксис:
```
 options = statset('OutputFcn',{@outfun, @outfun2});
```
Вызовите оптимизационную функцию с options как входной параметр.

Пример выходной функции см. в Sample Output Function.

Структура выходной функции

Линия определения функции выходной функции имеет следующую форму:

stop = outfun(beta,status,state)

где

beta - текущие фиксированные эффекты.
status - структура, содержащая данные текущей итерации. Поля в статусе подробно описывают структуру.
state - текущее состояние алгоритма. Состояния Алгоритма перечисляют возможные значения.
stop является флагом, который true или false в зависимости от того, должна ли стандартная программа оптимизации завершаться или продолжаться. Для получения дополнительной информации см. раздел «Стоп-флаг».

Решатель передает значения входных параметров в outfun при каждой итерации.

Поля в состоянии

В следующей таблице перечислены поля status структура:

Область	Описание
`procedure`	`'ALT'` - альтернативный алгоритм оптимизации линейных смешанных эффектов или ограниченных линейных смешанных приближений `'LAP'` - оптимизация лапласианского приближения для условной оценки первого порядка или первого порядка
`iteration`	Целое число, начиная с 0.
`inner`	Структура, описывающая статус внутренних итераций в `ALT` и `LAP` процедуры с полями: `procedure` - Когда `procedure` является `'ALT'`: `'PNLS'` (штрафуемые нелинейные методы наименьших квадратов) `'LME'` (оценка линейных смешанных эффектов) `'none'` Когда `procedure` является `'LAP'`, `'PNLS'` (штрафуемые нелинейные методы наименьших квадратов) `'PLM'` (профилированная максимизация вероятностей) `'none'` `state` - одно из следующих: `'init'` `'iter'` `'done'` `'none'` `iteration` - целое число, начинающееся от 0, или `NaN`. Для `nlmefitsa` с итерациями burn-in выходная функция вызывается после каждой из этих итераций с отрицательным значением для `STATUS.iteration`.
`fval`	Текущая вероятность журнала
`Psi`	Текущая ковариационная матрица случайных эффектов
`theta`	Текущая параметризация `Psi`
`mse`	Текущее отклонение ошибки

Состояния алгоритма

В следующей таблице перечислены возможные значения для state:

состояние	Описание
`'init'`	Алгоритм находится в начальном состоянии перед первой итерацией.
`'iter'`	Алгоритм находится в конце итерации.
`'done'`	Алгоритм находится в конечном состоянии после последней итерации.

Следующий код иллюстрирует, как выходная функция может использовать значение state чтобы решить, какие задачи выполнять при текущей итерации:

switch state
    case 'iter'
          % Make updates to plot or guis as needed
    case 'init'
          % Setup for plots or guis
    case 'done'
          % Cleanup of plots, guis, or final plot
otherwise
end

Стоп-флаг

Выходной аргумент stop является флагом, который true или false. Флаг сообщает решателю, должен ли он выйти или продолжить. В следующих примерах показаны типичные способы использования stop флаг.

Остановка оптимизации на основе промежуточных результатов. Выходная функция может остановить оценку при любой итерации, основанной на значениях переданных в нее аргументов. Например, следующий код устанавливает stop на true на основе значения вероятности журнала, сохраненного в 'fval'поле структуры статуса:

stop = outfun(beta,status,state)
stop = false;
% Check if loglikelihood is more than 132.
if status.fval > -132
    stop = true;
end

Остановка итерации на основе входа графический интерфейс пользователя. Если вы проектируете графический интерфейс пользователя для выполнения nlmefit итерации, можно сделать выходную функцию остановкой, когда пользователь нажимает кнопку Stop на графическом интерфейсе пользователя. Например, следующий код реализует диалоговое окно для отмены вычислений:

function retval = stop_outfcn(beta,str,status)
persistent h stop;
if isequal(str.inner.state,'none')
    switch(status)
        case 'init'
            % Initialize dialog
            stop = false;
            h = msgbox('Press STOP to cancel calculations.',...
                'NLMEFIT: Iteration 0 ');
            button = findobj(h,'type','uicontrol');
            set(button,'String','STOP','Callback',@stopper)
            pos = get(h,'Position');
            pos(3) = 1.1 * pos(3);
            set(h,'Position',pos)
            drawnow
        case 'iter'
            % Display iteration number in the dialog title
            set(h,'Name',sprintf('NLMEFIT: Iteration %d',...
                str.iteration))
            drawnow;
        case 'done'
            % Delete dialog
            delete(h);
    end
end
if stop
    % Stop if the dialog button has been pressed
    delete(h)
end
retval = stop;
 
    function stopper(varargin)
        % Set flag to stop when button is pressed
        stop = true;
        disp('Calculation stopped.')
    end
end

Выборочная выходная функция

nmlefitoutputfcn является образцом выходной функции Statistics and Machine Learning Toolbox для nlmefit и nlmefitsa. Он инициализирует или обновляет график с фиксированными эффектами (BETA) и отклонение случайных эффектов (diag(STATUS.Psi)). Для nlmefit, график также включает логарифмическую правдоподобность (STATUS.fval).

nlmefitoutputfcn - выходная функция по умолчанию для nlmefitsa. Использовать его с nlmefit, задайте для него указатель на функцию в структуре опций:

opt = statset('OutputFcn', @nlmefitoutputfcn, …)
beta = nlmefit(…, 'Options', opt, …)

Чтобы предотвратить nlmefitsa при использовании этой функции задайте пустое значение для выходной функции:

opt = statset('OutputFcn', [], …)
beta = nlmefitsa(…, 'Options', opt, …)

nlmefitoutputfcn останавливает nlmefit или nlmefitsa если вы закрываете рисунок, которую она создает.

Документация