Квадратичные поверхности отклика являются простыми моделями, которые обеспечивают максимум или минимум, не делая дополнительных предположений о форме отклика. Квадратичные модели могут быть калиброваны с помощью полных факториальных проектов с тремя или более уровнями для каждого фактора, но эти проекты обычно требуют большего запуски, чем необходимо для точной оценки параметров модели. В этом разделе рассматриваются проекты для калибровки квадратичных моделей, которые являются намного более эффективными, с использованием трех или пяти уровней для каждого фактора, но не с использованием всех комбинаций уровней.
Центральные композитные проекты (CCD), также известные как проекты Box-Wilson, подходят для калибровки полных квадратичных моделей. Существует три типа ПЗС - описанные, вписанные и сталкивающиеся - изображенные ниже:
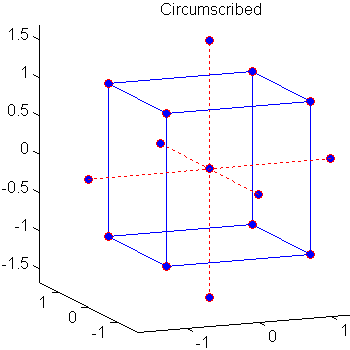
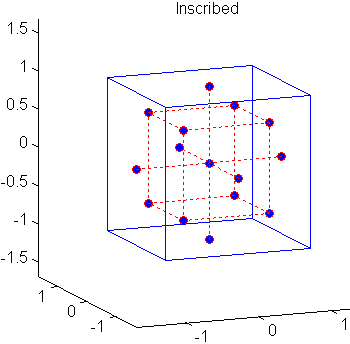
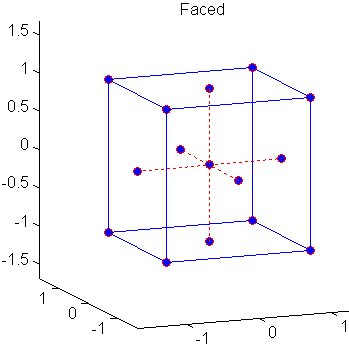
Каждый проект состоит из факториального проекта (углы куба) вместе с center и star точками, которые позволяют оценить эффекты второго порядка. Для полной квадратичной модели с n факторами CCD имеют достаточно проект точек, чтобы оценить (n + 2) (n + 1 )/2 коэффициентов в полной квадратичной модели с n факторами.
Тип используемого ПЗС (положение факториальной и звездной точек) определяется количеством факторов и желаемыми свойствами проекта. В следующей таблице приведены некоторые важные свойства. Проект rotatable, если отклонение предсказания зависит только от расстояния до точки проектирования от центра проекта.
| Проект | Способный вращаться | Уровни факторов | Использование точек снаружи ± 1 | Точность оценок |
|---|---|---|---|---|
| Описанный (CCC) | Да | 5 | Да | Хорошо по всему дизайнерскому пространству |
| Вписанный (CCI) | Да | 5 | Нет | Хорошо по центральному подмножеству проекта пространства |
| Лицом к лицу (CCF) | Нет | 3 | Нет | Ярмарка по всему дизайнерскому пространству; плохой для чистых квадратичных коэффициентов |
Сгенерируйте CCD с функцией ccdesign:
dCC = ccdesign(3,'type','circumscribed')
dCC =
-1.0000 -1.0000 -1.0000
-1.0000 -1.0000 1.0000
-1.0000 1.0000 -1.0000
-1.0000 1.0000 1.0000
1.0000 -1.0000 -1.0000
1.0000 -1.0000 1.0000
1.0000 1.0000 -1.0000
1.0000 1.0000 1.0000
-1.6818 0 0
1.6818 0 0
0 -1.6818 0
0 1.6818 0
0 0 -1.6818
0 0 1.6818
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0Повторные запуски центральных точек позволяют получить более равномерную оценку отклонения предсказания во всем проектном пространстве.
Как и проекты, описанные в Central Composite Designs, проекты Box-Bennken используются для калибровки полных квадратичных моделей. Проекты Box-Bhnken являются вращаемыми и, для небольшого количества факторов (четыре или меньше), требуют меньше запусков, чем CCD. Избегая углов проекта пространства, они позволяют экспериментаторам работать вокруг экстремальных комбинаций факторов. Однако, как и вписанная ПЗС, крайности затем оцениваются плохо.
Геометрия проекта Box-Behnken изображена на следующем рисунке.
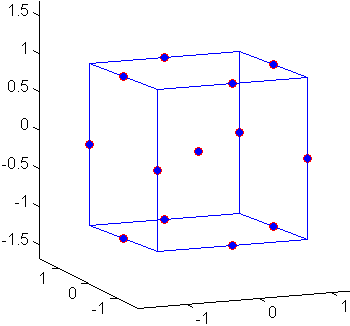
Проектные точки находятся в середине ребер проектного пространства и в центре и не содержат встроенного факториального проекта.
Сгенерируйте проекты Бокса-Бенкена с функцией bbdesign:
dBB = bbdesign(3)
dBB =
-1 -1 0
-1 1 0
1 -1 0
1 1 0
-1 0 -1
-1 0 1
1 0 -1
1 0 1
0 -1 -1
0 -1 1
0 1 -1
0 1 1
0 0 0
0 0 0
0 0 0Снова, повторные запуски центральных точек позволяют получить более равномерную оценку отклонения предсказания во всем проектном пространстве.