Прямое и обратное преобразования Фурье

На этой странице показан рабочий процесс преобразования Фурье и обратного Фурье в Symbolic Math Toolbox™. Для простых примеров смотрите fourier и ifourier. Здесь рабочий процесс для преобразований Фурье демонстрируется путем вычисления отклонения луча от силы. Связанное дифференциальное уравнение решается преобразованием Фурье.

Определение преобразования Фурье

Преобразование Фурье f (x) относительно x при w является

$F (w) = \int_{- \infty}^{\infty} f (x) e^{- i w x} d x .$

Обратное преобразование Фурье является

$f (x) = \frac{1}{2 π} \int_{- \infty}^{\infty} F (w) e^{i w x} d w .$

Концепция: Использование символьных рабочих процессов

Символьные рабочие процессы сохраняют вычисления в естественной символьной форме вместо числовой формы. Этот подход помогает вам понять свойства вашего решения и использовать точные символические значения. Вы подставляете числа вместо символьных переменных только тогда, когда вам требуется числовой результат или вы не можете продолжать символьно. Для получения дополнительной информации смотрите Выбрать числовую или символьную арифметику. Как правило, шаги следующие:

Объявить уравнения.
Решить уравнения.
Подстановочные значения.
Постройте график результатов.
Анализ результатов.

Вычислите отклонение луча с помощью преобразования Фурье

Задайте уравнения

Преобразование Фурье может использоваться, чтобы решить обыкновенные и дифференциальные уравнения с частными производными. Например, можно смоделировать отклонение бесконечно длинной балки, опирающейся на упругое основание под действием силы точки. Соответствующим реальным примером являются железнодорожные пути на фундаменте. Железнодорожные пути являются бесконечно длинной балкой, в то время как фундамент упругий.

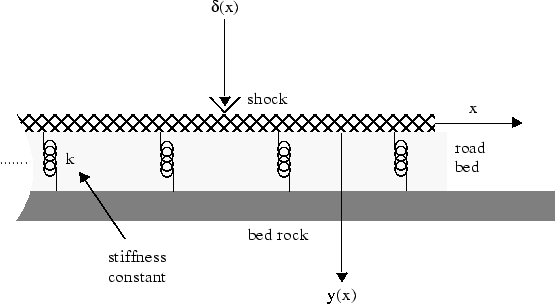
Давайте

E быть упругость балки (или железнодорожного пути).
I быть вторым моментом площади поперечного сечения балки.
k быть пружинная жесткость фундамента.

Дифференциальное уравнение

$\frac{d^{4} y}{d x^{4}} + \frac{k}{E I} y = \frac{1}{E I} δ (x), - \infty < x < \infty .$

Определите функцию y(x) и переменные. Предположим E, I, и k положительны.

syms Y(x) w E I k f
assume([E I k] > 0)

Назначьте модули при помощи symunit.

u = symunit;
Eu = E*u.Pa;    % Pascal
Iu = I*u.m^4;   % meter^4
ku = k*u.N/u.m^2;  % Newton/meter^2
X = x*u.m;
F = f*u.N/u.m;

Задайте дифференциальное уравнение.

eqn = diff(Y,X,4) + ku/(Eu*Iu)*Y == F/(Eu*Iu)

eqn(x) =
diff(Y(x), x, x, x, x)*(1/[m]^4) + ((k*Y(x))/(E*I))*([N]/([Pa]*[m]^6)) == ...
        (f/(E*I))*([N]/([Pa]*[m]^5))

Представление силового f по функции дельта-функции Dirac (x).

eqn = subs(eqn,f,dirac(x))

eqn(x) =
diff(Y(x), x, x, x, x)*(1/[m]^4) + ((k*Y(x))/(E*I))*([N]/([Pa]*[m]^6)) == ...
        (dirac(x)/(E*I))*([N]/([Pa]*[m]^5))

Решение уравнений

Вычислим преобразование Фурье eqn при помощи fourier по обеим сторонам eqn. Преобразование Фурье преобразует дифференциацию в экспоненты w.

eqnFT = fourier(lhs(eqn)) == fourier(rhs(eqn))

eqnFT =
w^4*fourier(Y(x), x, w)*(1/[m]^4) + ((k*fourier(Y(x), x, w))/(E*I))*([N]/([Pa]*[m]^6)) ...
        == (1/(E*I))*([N]/([Pa]*[m]^5))

Изолируйте fourier(Y(x),x,w) в уравнении.

eqnFT = isolate(eqnFT, fourier(Y(x),x,w))

eqnFT =
fourier(Y(x), x, w) == (1/(E*I*w^4*[Pa]*[m]^2 + k*[N]))*[N]*[m]

Вычислите Y(x) вычислением обратного преобразования Фурье правой стороны. Упростите результат.

YSol = ifourier(rhs(eqnFT));
YSol = simplify(YSol)

YSol =
((exp(-(2^(1/2)*k^(1/4)*abs(x))/(2*E^(1/4)*I^(1/4)))*sin((2*2^(1/2)*k^(1/4)*abs(x) + ...
        pi*E^(1/4)*I^(1/4))/(4*E^(1/4)*I^(1/4))))/(2*E^(1/4)*I^(1/4)*k^(3/4)))*[m]

Проверяйте это YSol имеет правильные размерности путем подстановки YSol в eqn и использование checkUnits функция. checkUnits возвращает логический 1 (true), что означает eqn теперь имеет совместимые модули измерения тех же физических размерностей.

checkUnits(subs(eqn,Y,YSol))

ans = 
  struct with fields:

    Consistent: 1
    Compatible: 1

Разделите выражение от модулей при помощи separateUnits.

YSol = separateUnits(YSol)

YSol =
(exp(-(2^(1/2)*k^(1/4)*abs(x))/(2*E^(1/4)*I^(1/4)))*sin((2*2^(1/2)*k^(1/4)*abs(x) + ...
        pi*E^(1/4)*I^(1/4))/(4*E^(1/4)*I^(1/4))))/(2*E^(1/4)*I^(1/4)*k^(3/4))

Подстановочные значения

Используйте значения E = 10⁶ Pa, I = 10^-3 m⁴, и k = 10⁶ Н/м². Замените эти значения на YSol и преобразовать в плавающую точку при помощи vpa с 16 цифрами точности.

values = [1e6 1e-3 1e5];
YSol = subs(YSol,[E I k],values);
YSol = vpa(YSol,16)

YSol =
0.0000158113883008419*exp(-2.23606797749979*abs(x))*sin(2.23606797749979*abs(x) + ...
        0.7853981633974483)

Графическое изображение результатов

Постройте график результата при помощи fplot.

fplot(YSol)
xlabel('x')
ylabel('Deflection y(x)')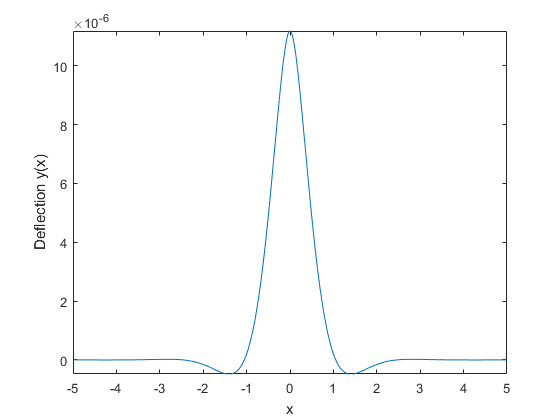

Анализ результатов

График показывает, что отклонение балки от точечной силы сильно локализовано. Отклонение наибольшее в точке влияния и затем быстро уменьшается. Символьный результат позволяет вам анализировать свойства результата, что невозможно с числовыми результатами.

Заметьте, что YSol является продуктом терминов. Термин с sin показывает, что реакция является вибрационным колебательным поведением. Термин с exp показывает, что колебательное поведение быстро затухает экспоненциальным распадом, когда расстояние от точки влияния увеличивается.

Документация