Непрерывное преобразование Вейвлета как полосно-пропускающий фильтр

CWT как метод фильтрации

Непрерывное вейвлет (CWT) вычисляет скалярное произведение сигнала, $f (t)$ с переведенными и расширенными версиями анализирующего вейвлета, $ψ (t) .$ Определение CWT:

$C (a, b; f (t), ψ (t)) = \int_{- \infty}^{\infty} f (t) \frac{1}{a} ψ^{*} (\frac{t - b}{a}) d t$

Можно также интерпретировать CWT как частотную фильтрацию сигнала, переписав CWT как обратное преобразование Фурье.

$C (a, b; f (t), ψ (t)) = \frac{1}{2 π} \int_{- \infty}^{\infty} \hat{f} (ω) \bar{\hat{ψ}} (a ω) e^{i ω b} d ω$

где $\hat{f} (ω)$ и $\hat{ψ} (ω)$ являются преобразованиями Фурье сигнала и вейвлет.

Из предыдущих уравнений можно увидеть, что растяжение вейвлета во времени заставляет его поддержку в частотный диапазон сокращаться. В дополнение к уменьшению поддержки частоты центральная частота вейвлета смещается в сторону более низких частот. Следующий рисунок демонстрирует этот эффект для гипотетических вейвлет и масштабных (расширительных) факторов 1,2 и 4.

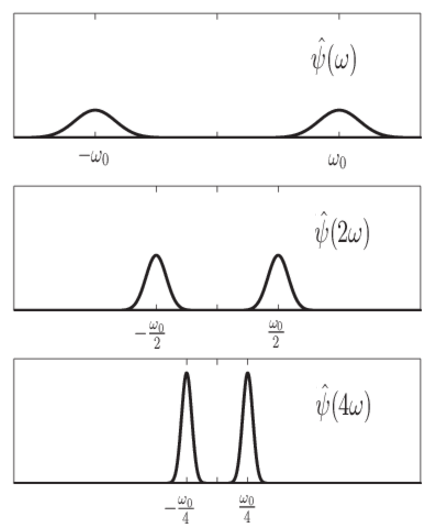
Это изображает CWT как полосно-пропускающую фильтрацию входного сигнала. Коэффициенты CWT в более низких шкалах представляют энергию в входном сигнале на более высоких частотах, в то время как коэффициенты CWT в более высоких шкалах представляют энергию в входном сигнале на более низких частотах. Однако, в отличие от полосно-пропускающей фильтрации Фурье, ширина полосно-пропускающего фильтра в CWT обратно пропорциональна шкале. Ширина фильтров CWT уменьшается с увеличением шкалы. Это следует из отношений неопределенности между временем и поддержкой частоты сигнала: чем шире поддержка сигнала во времени, тем более узкая его поддержка по частоте. Обратная связь также сохранена.

В вейвлет шкала или расширения задана для сохранения энергии. Для сохранения энергии при сокращении поддержки частоты требуется, чтобы пиковый уровень энергии увеличился. Реализация cwt в Wavelet Toolbox™ использует L1 нормализацию. Коэффициент качества, или Q-коэффициент фильтра, является отношением его пиковой энергии к ширине полосы пропускания. Поскольку уменьшение или растяжение частотной поддержки вейвлета приводит к соразмерным увеличениям или уменьшению его пиковой энергии, вейвлеты часто называют фильтрами с константой Q.

Непрерывное преобразование

Вейвлета на основе DFT

Уравнение в предыдущем разделе задало CWT как обратное преобразование Фурье продукта преобразований Фурье.

$C (a, b; f (t), ψ (t)) = \frac{1}{2 π} \int_{- \infty}^{\infty} \overset{\land}{f} (ω) {\hat{ψ}}^{*} (a ω) e^{j ω b} d ω$

Временная переменная в обратном преобразовании Фурье является параметром преобразования, b.

Это предполагает, что вы можете вычислить CWT с обратным преобразованием Фурье. Поскольку существуют эффективные алгоритмы для расчета дискретного преобразования Фурье и его обратного, вы часто можете достичь значительной экономии при помощи fft и ifft когда это возможно.

Чтобы получить изображение CWT в области Фурье, начните с определения вейвлет:

$< f (t), ψ_{a, b} (t) > = \frac{1}{a} \int_{- \infty}^{\infty} f (t) ψ^{*} (\frac{t - b}{a}) d t$

Если вы задаете:

${\tilde{ψ}}_{a} (t) = \frac{1}{a} ψ^{*} (- t / a)$

можно переписать вейвлет как

$(f * {\tilde{ψ}}_{a}) (b) = \int_{- \infty}^{\infty} f (t) {\tilde{ψ}}_{a} (b - t) d t$

который явно выражает CWT как свертку.

Чтобы реализовать дискретизированную версию CWT, примите, что входная последовательность является вектором длины N, x[n]. Дискретная версия предыдущей свертки:

$W_{a} [b] = \sum_{n = 0}^{N - 1} x [n] {\tilde{ψ}}_{a} [b - n]$

Чтобы получить CWT, похоже, что вы должны вычислить свертку для каждого значения параметра shift, b и повторить этот процесс для каждой шкалы, a.

Однако, если две последовательности расширены по кругу (периодически до длины N), можно выразить круговую свертку как продукт дискретных преобразований Фурье. CWT является обратным преобразованием Фурье продукта

$W_{a} (b) = \frac{1}{N} \sqrt{\frac{2 π}{Δ t}} \sum_{k = 0}^{N - 1} \overset{\land}{X} (2 π k / N Δ t) \overset{\land}{ψ} * (a 2 π k / N Δ t) e^{j 2 π k b / N}$

где И t - интервал дискретизации (период).

Выражение CWT как обратного преобразования Фурье позволяет вам использовать вычислительно-эффективное fft и ifft алгоритмы для снижения затрат на вычисление сверток.

cwt функция реализует CWT.

Документация